* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lecture 17: Ampere`s law
Neutron magnetic moment wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electrical resistance and conductance wikipedia , lookup
Magnetic monopole wikipedia , lookup
Maxwell's equations wikipedia , lookup
Field (physics) wikipedia , lookup
Magnetic field wikipedia , lookup
Electromagnetism wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Superconductivity wikipedia , lookup
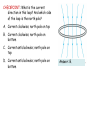
CHECKPOINT: What is the current direction in this loop? And which side of the loop is the north pole? A. Current clockwise; north pole on top B. Current clockwise; north pole on bottom C. Current anticlockwise; north pole on top D. Current anticlockwise; north pole on bottom Answer: B. Last lecture Magnetic force between parallel wires (p445) The magnetic field B1 due to current I1 is perpendicular to current I2. The force on current I2 is towards current I1. dF2 I 2 dl 2 B1 There is an equal an opposite force exerted by current I2 on I1. The wires thus attract each other. If current I1is reversed, B1 would be in opposite direction. Therefore we find that antiparallel currents repel. Gauss’ law for magnetism Got it? Which could be a magnetic field? 26.8 Ampère’s law We found for highly symmetric charge distributions, we could calculate the electric field more easily using Gauss’s Law than Coulomb’s Law. Similarly Ampère’s Law relates to the tangential component Bt of the magnetic field summed (integrated) around a closed curve C the current IC that passes through any surface bounded by C. Iencircled is the net current that penetrates the surface bounded by the curve C. B ds B cos ds I 0 enclosed C As in Gauss’s law, the field that appears in the integral is the net field arising from all sources, not just the encircled currents. We can now use Ampère’s Law for situations where symmetry allows us to simplify, and solve the integral for the magnetic field. B dl B dl C The simplest case is for an infinite long, straight, currentcarrying wire. Choose the circular curve centred on wire. Magnetic field is tangent to this circle from BiotSavart law, and has the same magnitude all around the loop. B d l B dl B2 R i 0 enclosed C 0ienclosed B 2 R Compare with earlier result using Biot-Savart: Magnetic field B due to a current in a straight wire. B 0 I 2a 4 x x 2 a 2 If the length of the wire approaches infinity in both directions, we found A.True F. False Magnetic fields 1. The magnetic field due to a current element is parallel False to the current element. 2. The magnetic field due to a current element varies inversely with the square of the distance from the element. 3. The magnetic field due to a long wire varies inversely with the square of the distance from the wire. 4. Ampere’s law is valid only of there is a high degree of False symmetry. True False Solar currents Example 26.7 Ampere’s law: solar currents Applications of Ampere’s Law Ex 26.8 Field outside and inside a long straight currentcarrying wire Ex 26.9 Field outside a current sheet Ex 26.10 Field of a solenoid Fig 26.39 Field of a toroidal solenoid EXAMPLE 26.8: A long straight wire of radius R carries a current I that is uniformly distributed over the circular cross section of the wire. Find the magnetic field both (a) outside and (b) inside the wire. I I