Download Lecture 17: Ampere`s law

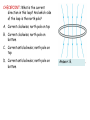
CHECKPOINT: What is the current
direction in this loop? And which side
of the loop is the north pole?
A. Current clockwise; north pole on top
B. Current clockwise; north pole on
bottom
C. Current anticlockwise; north pole on
top
D. Current anticlockwise; north pole on
bottom
Answer: B.
Last lecture
Magnetic force between parallel wires (p445)
The magnetic field B1 due to current I1 is perpendicular to
current I2.
The force on current I2 is towards current I1.
dF2  I 2 dl 2  B1
There is an equal an opposite force exerted by current I2 on I1.
The wires thus attract each other.
If current I1is reversed, B1 would be in opposite
direction. Therefore we find that antiparallel
currents repel.
Gauss’ law for magnetism
Got it? Which could be a magnetic field?
26.8 Ampère’s law
We found for highly symmetric charge distributions, we
could calculate the electric field more easily using Gauss’s
Law than Coulomb’s Law.
Similarly Ampère’s Law relates
to
the tangential component Bt of the magnetic field
summed (integrated) around a closed curve C
the current IC that passes through any surface
bounded by C.
Iencircled is the net current that penetrates
the surface bounded by the curve C.
 B  ds  B cos ds   I
0 enclosed
C
As in Gauss’s law, the field that appears in the integral is the net field
arising from all sources, not just the encircled currents.
We can now use Ampère’s Law for situations where symmetry allows us
to simplify, and solve the integral for the magnetic field.
 B  dl  B  dl
C
The simplest case is for an
infinite long, straight, currentcarrying wire.
Choose the circular curve
centred on wire. Magnetic field is
tangent to this circle from BiotSavart law, and has the same
magnitude all around the loop.
 B  d l  B  dl  B2 R   i
0 enclosed
C
0ienclosed
B
2 R
Compare with earlier result using Biot-Savart:
Magnetic field B due to a current in a straight wire.
B
0 I
2a
4 x x 2  a 2
If the length of the wire
approaches infinity in both
directions, we found
A.True
F. False
Magnetic fields
1.
The magnetic field due to a current element is parallel
False
to the current element.
2.
The magnetic field due to a current element varies
inversely with the square of the distance from the
element.
3.
The magnetic field due to a long wire varies inversely
with the square of the distance from the wire.
4.
Ampere’s law is valid only of there is a high degree of
False
symmetry.
True
False
Solar currents
Example 26.7 Ampere’s law: solar currents
Applications of Ampere’s Law
Ex 26.8
Field outside and inside a long straight currentcarrying wire
Ex 26.9
Field outside a current sheet
Ex 26.10
Field of a solenoid
Fig 26.39
Field of a toroidal solenoid
EXAMPLE 26.8: A long straight wire of
radius R carries a current I that is uniformly
distributed over the circular cross section of
the wire. Find the magnetic field both (a)
outside and (b) inside the wire.
I
I