Download Carroll County Middle School

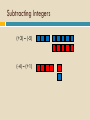
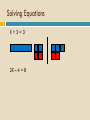
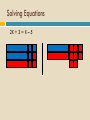
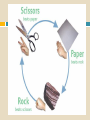
CARROLL COUNTY
MIDDLE
SCHOOL
Math Department Professional
Development
February 5, 2010
Number Line Problems…


Having a number line in the room at all times allows
for innumerous opportunities to work on number
sense.
Number Sense is essential for success in all areas of
mathematics
Number Line I

The points on the number line below are evenly spaced.
On the number line above, -2 is located at C and 1 is located at I.
1. What is the location of 0
(zero)?
2. What is the location of -3?
3. What is the location of ½ ?
4. What is the location of -2
½?
5. What is the location of -1
½ ?
Number Line II

The points on the number line below are evenly spaced.
On the number line above, 3 is at the position labeled C
and 4 is at H.
1. What is the coordinate of 2. What is the coordinate of
D?
G?
3. What is the coordinate of 4. What is the coordinate of
I ?
A ?
Number Line III

The points on the number line below are evenly spaced.
On the number line above, 0.0019 is the coordinate of point B
and 0.0085 is the coordinate of point H.
1. What is the coordinate of C ? 2. What is the coordinate of E?
3. What is the coordinate of A?
5. What is the coordinate of F?
4. What is the coordinate of G?
Number Line IV

The points on the number line below are evenly spaced.
1. What is the coordinate of
point E?
2. What is the coordinate of
point B?
3. What is the coordinate of
point C?
4. What is the coordinate of
point H?
5. What is the coordinate of
point A?
6. What is the coordinate of
point F?
Number Line V

The points on the number line below are evenly spaced.
1. What is the coordinate of point A as a
percent?
2. What is the coordinate of point A as a
decimal?
3. What is the coordinate of point D as a
percent?
4. What is the coordinate of point J as a
decimal?
Number Line Problems…


Having a number line in the room at all times allows
for innumerous opportunities to work on number
sense.
Number Sense is essential for success in all areas of
mathematics
Reflection…
LET’S DO
ALGEBRA TILES
Algebra Tiles




Talking partners or groups enhance student
understanding. It’s imperative we have students talk
about their work!
When I listen, I hear.
When I see, I remember.
But when I do, I understand.
Algebra Tiles



Algebra tiles can be used to model
operations with integers.
Let the small blue square represent +1 and
the small red square represent -1.
The blue and red squares are additive
inverses of each other.
Zero Pairs


Zero pairs are additive inverses.
When put together, they “cancel” each other out to
model zero.
Addition of Integers




Addition can be viewed as “combining”.
Combining involves the forming and removing of all
zero pairs.
For each of the given examples, use algebra tiles to
model the addition.
Draw diagrams which show the modeling.
Addition of Integers
(+3) + (+1) =
(-2) + (-1) =
Addition of Integers
(+3) + (-1) =
(+4) + (-4) =

After students have seen many examples of
addition, have them formulate rules.
Subtraction of Integers




Subtraction can be interpreted as “take-away.”
Subtraction can also be thought of as “adding the
opposite.”
For each of the given examples, use algebra tiles to
model the subtraction.
Draw pictorial diagrams which show the modeling
process.
Subtraction of Integers
(+5) – (+2) =
(-4) – (-3) =
Subtracting Integers
(+3) – (-5)
(-4) – (+1)
Subtracting Integers
(+3) – (-3)

After students have seen many examples, have them
formulate rules for integer subtraction.
Multiplication of Integers




Integer multiplication builds on whole number
multiplication.
Use concept that the multiplier serves as the number of
sets needed.
For the given examples, use the algebra tiles to model the
multiplication. Identify the multiplier.
Draw diagrams which model the multiplication process.
Multiplication of Integers

The counter indicates how many rows to make. It
has this meaning if it is positive.
(+2)(+3) =
(+3)(-4) =
Multiplication of Integers

If the counter is negative it will mean “take the
opposite of.”
(-2)(+3)
(-3)(-1)
Multiplication of Integers


After students have seen many examples, have them
formulate rules for integer multiplication.
Have students practice applying rules abstractly
with larger integers.
Division of Integers



Like multiplication, division relies on the concept of a
counter.
Divisor serves as counter since it indicates the
number of rows to create.
For the given examples, use algebra tiles to model
the division. Identify the divisor or counter. Draw
pictorial diagrams which model the process.
Division of Integers
(+6)/(+2) =
(-8)/(+2) =
Division of Integers

A negative divisor will mean “take the opposite of.”
(flip-over)
(+10)/(-2) =
Division of Integers
(-12)/(-3) =

After students have seen many examples, have them
formulate rules.
Solving Equations



Algebra tiles can be used to explain and justify the
equation solving process. The development of the
equation solving model is based on two ideas.
Variables can be isolated by using zero pairs.
Equations are unchanged if equivalent amounts are
added to each side of the equation.
Solving Equations

Use the blue rectangle as X and the red rectangle
as –X (the opposite of X).
X+2=3
2X – 4 = 8
2X + 3 = X – 5
Solving Equations
X+2=3
2X – 4 = 8
Solving Equations
2X + 3 = X – 5
Distributive Property
Use the same concept that was applied with
multiplication of integers, think of the first factor as
the counter.
 The same rules apply.
3(X+2)
 Three is the counter, so we need three rows of (X+2)

Distributive Property
3(X + 2)
3(X – 4)
-2(X + 2)
-3(X – 2)
This material was modified from work done by
David McReynolds
AIMS PreK-16 Project
Noel Villarreal
South Texas Rural Systemic Initiative
Affiliated with
The Dana Center
Now
Education World Math Center
http://www.educationworld.com/math/
Reflection…
Take a Break
Something to think about….
New research from Vanderbilt University has found
students benefit more from being taught the
concepts behind math problems rather than the
exact procedures to solve the problems.
ScienceDaily (Apr. 12, 2009)
News Flash
• All students can and should learn math!
• If children like math and feel successful at
they will learn math!
math -
• there are 3 stages that children go through when
learning math:
–Stage 1: Using Manipulatives
–Stage 2: Developing a Mental Image
–Stage 3: Using Symbols
Students need to……
Build
it! Concrete
Draw it! Mental Image
Write it! Symbolic
SAY IT throughout
Game Time…. What’s the point?
This is a game for 2 or more players.
Materials: What’s Your Point cards, game board, and a different color dry erase marker for
each player
The object is to get 3 linear points – the points do not have to be
consecutive.
1. Deal each player 5 cards.
2. Place all of the other cards face down in a pile.
3. Take turns.
On your turn, play one of the cards from your hand by laying it down and marking that
point on the coordinate grid with your color marker. Replace that card by drawing a card
from the deck.
The winner is the first player to get 3 linear points.
Optional versions:
The winner is the first player to get 3 linear points and correctly gives the slope.
The winner is the first player to get 3 linear points and correctly gives the equation.
Website Exploration
www.illuminations.org
While there find an activity or lesson for the topic you are
on.
Also look at Dynamic Paper while there
www.educationworld.com/math/
This site is worth some exploration
www.ket.org/scalecity/index.html
This has great potential for ratios, rates, and proportions
nlvm.usu.edu/en/nav/vlibrary.html
Take a look and explore the data analysis and prob.
Let’s Eat
Target


Choose a number such
as 456
Choose a smaller
number to be the
target such as 26

Your goal is to get as close to
the target as you can by using
the following rules:





On each round, you can only
add, subtract, multiply, or
divide by 10
You can use as many rounds
as you like
Stop when you think you are
as close to the target as you
can get
The winner is the player that
is closer to the target
In case of a tie, the winner is
the person that used the
fewest rounds
Triangle or Not?


Randomly generated
three numbers on
number cubes, or
calculator.
Determine if the three
numbers rolled can be
the sides of a triangle.


Keep a frequency
table based on repeat
results. (50)
What is the
probability of rolling
three numbers which
can form a triangle?
A Fair Game? The Case of Rock,
Paper, Scissors
NCTM Standards for this activity…
• Develop and evaluate inferences
and predictions that are based on
data
• Understand and apply basic concepts
of probability
What’s your prediction?

Is the game fair?

Or not?