* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 6 Notes
Survey
Document related concepts
Transcript
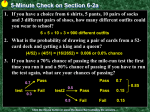
AP Statistics
Chapter 6 Notes
Probability Terms
Random: Individual outcomes are uncertain, but there
is a predictable distribution of outcomes in the long
run.
Probability: long term relative frequency
Sample Space: The set of all possible outcomes of a
random phenomenon.
Sample space for rolling one die
S = {1, 2, 3, 4, 5, 6}
Sample space for the heights of adult males
S = {all real x such that 30in < x < 100in}
Ways to determine Sample Space
1. Tree diagram
2. Multiplication Principle: If one task can be
done n1 number of ways and another can be
done n2 number of ways, then both tasks can be
done in n1 × n2 number of ways.
3. Organized list
Events
Any outcome or set of outcomes of a random
phenomenon. (It is a subset of the sample
space).
Ex: rolling a 1
Ex: rolling a 2 or 3
Ex: Randomly choosing an adult male between
60 and 65 inches tall.
Other probability terms
Sampling with replacement: Each pick is the
same…(number goes back in the hat).
Sampling without replacement: Each draw is
different.
Mutually exclusive/disjoint: Two (or more)
events have no outcomes in common and thus
can never occur simultaneously.
Complement: The complement of any event,
A, is the event that A does not occur. (Ac)
Basic Probability Rules
1. For any event, A, 0 < P(A) < 1.
2. If S is the sample space, then P(S) = 1.
3. Addition Rule: If A and B are disjoint, then
P(A or B) = P(A U B) = P(A) + P(B)
4. Complement Rule: P(Ac) = 1 – P(A)
Set Notation
More Set Notation
Independence
Independence: Knowing that one event occurs
does not change the probability that the other
event occurs.
5. Multiplication Rule
If events A and B are independent, then
P(A and B) = P(A ∩ B) = P(A) × P(B)
General Addition Rule
Reminder….addition rule for mutually exclusive
events is…
P(A U B U C….) = P(A) + P(B) + P(C) + …
The General Addition Rule applies to the union
of two events, disjoint or not.
P(A or B) = P(A) + P(B) – P(A and B)
P(A U B) = P(A) + P(B) – P(A ∩ B)
Conditional Probability
P(A|B) “The probability of event A given that event
B has occurred.”
Examples:
One card has been picked from a deck. Find…
One dice has been rolled. Find…
P(spade|black), P(queen|face card)
P(3|odd), P(odd|prime)
Two dice are rolled. Find P(2nd die is 4|1st die is 3).
New definition of independence: Events A and B are
independent if P(A) = P(A|B).
General Multiplication Rule
Reminder….Multiplication Rule for independent
events is…
P(A ∩ B) = P(A) × P(B)
The General Multiplication Rule applies to the
intersection of two events, independent or not.
P(A ∩ B) = P(A) × P(B|A)
P(A ∩ B) = P(B) × P(A|B)
Why does this rule also work for independent
events?
Conditional Probability Formula
Using algebra, we can rearrange the general
multiplication rule to write a formula for
conditional probability.
P(B|A) = P(A ∩ B) ÷ P(A)
P(A|B) = P(A ∩ B) ÷ P(B)