Download Coordinates Geometry

Mathematics Competition Training Class Notes
Coordinates Geometry
Coordinates Geometry
Precaution: This chapter requires some knowledge in Elementary Geometry.
Coordinates System
Locating a point: Introduction the coordinates system
In mathematics and daily life we often need to describe the position of an object. But
mostly the description is imprecise, for example:
How would you describe the location of the gray circle? It is above the red line and on
the right of the blue line. But there is a problem: this description occupies a large area,
but the circle is only a small object inside it. That means this method is not suitable to
find out the actual position of an object. One solution is to tell exactly how far the
object is from the referencing ones. For example, the gray circle is 0.8 cm above the
red line and 1.3 cm on the right of the blue line. This will determine a unique point on
the plane and thus the object is accurately positioned. This is an example of
coordinates system. In a coordinates system defined on a plane, a point can be
defined precisely by a pair of numbers. This pair of numbers is called the coordinates
of the point. In our example above the system is called a rectangular coordinates
system. This system is constructed by followings:
1. Create a horizontal real line. Identify the zero on it, and make the positive side
points right.
2. Create another vertical real line that its zero matches the horizontal one. Make
the positive side points up.
y
2
(2, 1)
1
x
-1
0
1
2
3
4
5
The horizontal real line is called the x-axis and is marked with a letter “x”. Similarly,
108
Mathematics Competition Training Class Notes
Coordinates Geometry
the vertical real line is called the y-axis. The intersection of the two axes is called the
origin, which is marker with a letter “O”. In this system if we place an object, then we
can move this horizontally until reaching the y-axis. The point it coincide with the
y-axis is called the ordinate or y-coordinate of the object. Likewise, we can move the
object vertically and arrive at the x-axis. The point is called the abscissa or
x-coordinate. For the figure on the last page, the x-coordinate of black circle is 2 and
the y-coordinate is 1. If the x- and y-coordinate of a point is ζ and η respectively, then
the coordinates of this point are (ζ, η).
Conversely, if we consider the coordinates system is the set of all points on a plane,
then this set is defined as {(x, y) | x, y ∈ R}. However, this is also the definition of R2.
Therefore, the set R2 and the coordinates system is actually the same thing. From now
on, when we say R2 it means the coordinates system unless otherwise specified.
The coordinates system can be divided into four parts by the two axes. Each part is
called a quadrant. As shown below, the part {(x, y) | x, y ∈ R+} is called quadrant I,
{(x, y) | x ∈ R–, y ∈ R+} is called quadrant II, etc. The axes are not included in any
quadrant.
II
I
III
IV
Application of the coordinates system*
The coordinates system is useful in solving geometrical problems and algebraic
equations. The first use is obvious. We can plug the geometric figures into the system
directly. And for algebraic equations, we can draw curves about the equations and find
the corresponding intersections in the system (to be discussed in the next section).
109
Mathematics Competition Training Class Notes
Coordinates Geometry
Line Segment
Curves on the coordinates system
Curves are one-dimensional objects that is “bent” from a line or line segment. Circles,
lines are examples of curves.
Example of curves
In coordinates system, the shape of a curve can be described by collection of points.
For example, the red points below are some points that can make up a circle, and the
green curve is the “circle” created by infinite points like that.
y
1
0.5
x
0
0.5
1
We can say a curve in the coordinates systems is a set of points that satisfies some
predefined conditions. That means a curve C is a subset of R2 that is equals to
{( x, y ) ∈ ℝ
2
}
f ( x, y ) = 0
for some function f: R2 → R. Since only f is important in
how the curve is shaped, this curve is usually just denoted “f(x, y) = 0”. The following
show two curves. The purple one is y = x (that is the same as x – y = 0) and the green
one is y = x2.
110
Mathematics Competition Training Class Notes
Coordinates Geometry
y
4
2
x
-2
0
2
Line segments
Line segments are a special kind of curve that is not “curved” at all, and the length is
finite.
Examples of line segments
It is guaranteed that the shortest path that an object travels from one point to another
is a line segment and there is only one unique line segment for this. That means two
points on the coordinates system are enough to fix a line segment. Problems involving
line segments are usually “how long is that segment?” or “how steep is that segment?”
or “what is the area of a polygon enclosed by n segments?” or something like these.
In this section we will go in depth answering these questions.
Length of segment
(x1, y1)
(12.1)
y1 – y2
(x2, y2)
x1 – x2
In the figure there is a line segment ended with two points (x1, y1) and (x2, y2). The
length of the segment is easy to find. As figured we assume the segment is the
hypotenuse of a right triangle as shown. Then by Pythagoras’ theorem we have:
Length of segment =
( x1 − x2 )
111
2
+ ( y1 − y2 )
2
(12.2)
Mathematics Competition Training Class Notes
Coordinates Geometry
Example 12a: Show that the points (2, 1), (3, 8) and (5, 2) forms a right triangle.
Solution 12a:
Let A = (2, 1), B = (3, 8) and C = (5, 2). By (11.2), we have got:
AB = 50
BC = 40
(12.3)
CA = 10
Therefore, by the converse of Pythagoras’ theorem, ∆ABC is a right triangle.
Q.E.D.
Slope of segment
A measure of steepness is to find out the rise in one horizontal step for a segment. We
define this measure to be the slope of the segment. In the following, the red segment
has slope 0.5, the blue has slope 1 and green has slope 3.
3
2
1
1
However, the horizontal distance of the two end points may not be 1. To solve this, we
can shrink or enlarge the segment to have horizontal distance to be 1. If the original
horizontal distance is X, then the rise will be divided by X after the dilation. Referring
to the notation in (11.1), the slope of a line segment is defined as:
y1 − y2
(12.4)
x1 − x2
But the equation may give negative value. By definition, a negative slope means the
segment is “falling”:
Positive / Rise
Slope > 0
Slope < 0
Negative / Fall
If the slope of a segment is 0, then it is “flat”, i.e., horizontal. The slope for a vertical
segment is not defined, because there can never be any “horizontal step”.
112
Mathematics Competition Training Class Notes
Coordinates Geometry
Point of division
Given a line segment we can always cut it into two different segments. The place of
the cut is called the point of division. A common question is, “how to determine the
point of division if I want to divide the segment into ratio r : s?”. This can be easily
done with help of coordinate geometry.
Example 12b: Find out the formula for determining the point of division.
r:s
Solution 12b:
First of all, observe that the ratio does not change if we project the segment onto
either axis. Thus, we may find out the point of division of the projection on the two
axes to determine the coordinates of the point of division of the segment.
r:s
r:s
Now assume the end points of the green segment are (x1, y1) and (x2, y2), and the point
of division is (x0, y0). So, on the blue segment, the point x0 divides the interval [x1, x2]
x −x
x − x0
r
r
and 2
. Solving both
into ratio r : s. This means 0 1 =
=
x2 − x1 r + s
x2 − x1 r + s
equations give x0 =
rx2 + sx1
ry + sy1
. Similarly, y0 = 2
. Therefore:
r+s
r+s
 rx + sx1 ry2 + sy1 
,
divides the segment
The point  2
r + s 
 r+s
Connecting (x1, y1) and (x2, y2) into ratio r : s.
(12.5)
The formula (12.5) is known as the section formula. In particular, if the point divides
the segment into ratio 1:1, i.e., the point is the midpoint of the segment, then its
coordinates are:
 x1 + x2 y1 + y2 
(12.6)
 2 , 2 


This is called the midpoint formula.
External division
Till now we can only cut the segment inside it into ratio r : s. But we can also “cut”
the segment outside, and also result in ratio r : s. Consider the segment connecting the
113
Mathematics Competition Training Class Notes
Coordinates Geometry
AP 1
3 
= , the coordinates of P can be  , 0 
OP 3
4 
by section formula. But P can also be (3, 0) and the ratio is still 1 : 3. Such a point that
origin and A = (2, 0). For a point P that
“cut” the segment outside it is called an external point of division. Likewise, the one
that cut inside it is an internal point of division. To classify the external and internal
point of division, we define the external one divides a negative ratio. In our example,
the P divides the segment into ratio 1 : -3. With this definition, the section formula
holds for external point of division as well.
Example 12c: Given two points A (5, 6) and B (-2, 5). If a point P (x, -1) divides the
segment AB into ratio r : s with r < s, find:
r:s
x
Solution 12c:
Applying the section formula we have −1 =
5r + 6 s
. Solving this gives r : s = -7 : 6.
r+s
Apply section formula again gives x = -44.
Example 12d: Show that the point A (1, 1.5), B (-4, 2) and C (3, 1) are not collinear.
Solution 12d:
Assume A, B and C are collinear. Then C must be a point of division of AB, no matter
internal or external. So let the ratio be r : s. By section formula, for y-coordinates,
1.5 =
r + 2s
, thus
r+s
r : s = 1 : 1. However, for x-coordinates, 1 =
implies r : s = 5 : 2, a contradiction.
3r − 4 s
, which
r+s
Q.E.D.
Area of polygon enclosed by segments
Area of triangle
A triangle is form by three joined segments, which in turn is defined by three distinct
points. Thus we can find the area of a triangle using the coordinates of the points.
Example 12e: Given three points A (x1, y1), B (x2, y2) and C (x3, y3). Find the area of
∆ABC.
114
Mathematics Competition Training Class Notes
Coordinates Geometry
Solution 12e:
Enclose a rectangle ARQP around ∆ABC, and without loss of generality assume A is
the one of the vertices.
A (x1, y1)
P (x3, y1)
C (x3, y3)
R (x1, y2)
Q (x3, y2)
B (x2, y2)
From the figure, we have:
AP = x3 − x1
RB = x2 − x1
BQ = x3 − x2
Therefore, the area of ∆ACP =
AR = y2 − y1
PC = y3 − y1
CQ = y2 − y3
( x3 − x1 )( y3 − y1 )
2
, ∆BQC =
(12.7)
( x3 − x2 )( y2 − y3 )
2
,
( x2 − x1 )( y2 − y1 )
and ARQP = ( x3 − x1 )( y2 − y1 ) . But area of ∆ABC =
2
ARQP – ∆ACP – ∆BQC – ∆ARB. Therefore, after simplifying, the area of ∆ABC is:
∆ARB =
x1 y2 − x2 y1 + x2 y3 − x3 y2 + x3 y1 − x1 y3
2
(12.8)
(12.8) is not easy to remember. So we define:
a1
a2
a3
⋮
an
b1
b2
n −1 a
b3 = ∑ k
k =1 ak +1
⋮
bn
n −1
bk
= ∑ ak bk +1 − ak +1bk
bk +1 k =1
(12.9)
So the area of triangle is:
x1
1 x2
2 x3
x1
115
y1
y2
y3
y1
(12.10)
Mathematics Competition Training Class Notes
Coordinates Geometry
Example 12f: Redo example 12d.
Solution 12f:
If A, B and C are collinear then the area of ∆ABC should be zero. But area of ∆ABC =
3 1
1 1 1.5
= 0.75 ≠ 0 , so A, B, C are not collinear.
Q.E.D.
2 −4 2
3
1
Note that when using (12.10) please ensure the points are arranged counterclockwise.
Otherwise a negative value will be obtained. If you don’t know whether the points are
counterclockwise or not, take an absolute value.
Area of polygon
A polygon can be dissected into triangles. So we can just find out the area of each
triangle and sum up them to give the area of the polygon. In fact, if the vertices of the
polygon is (x1, y1), (x2, y2), …, (xn, yn) in counterclockwise order, then its area is:
x1
x2
1
⋮
2
xn
x1
y1
y2
⋮
yn
y1
 1 1
Example 12g: Let X be  − ,  , Y be
 2 2
2
y = 3 – x and P be a point on C in
(12.11)
 2 1
 ,  , O be the origin, C be the curve
 3 3
quadrant I. Find the maximum area of
quadrilateral OYPX.
Solution 12g:
Let P be (x, y). So 0 < x < 3 . Then:
0
0
23 13
1
Area of OYPX =
x
y
2
−1 2 1 2
0
0
=
1 2y − x x + y
+
2 3
2
=
1 x + 7y
2 6
116
(12.12)
Mathematics Competition Training Class Notes
=
Coordinates Geometry
x + 21 − 7 x 2
12
7 x − 7x − 3
2
=
7
=
12
12
2
1  589

x−  −
14  196

7 589 
1
=
−x− 
12 196 
14 
2
7 589
12 196
589
=
336
≤
Equality occurs when x = 1⁄14. Thus, the maximum area is 589⁄336.
117
Mathematics Competition Training Class Notes
Coordinates Geometry
Lines
Lines in coordinates system
Lines are curves that are straight and infinite in length. There are no end points for
lines. (A “line” with two end points is a segment, and one is a ray.) A line can be
thought as an extension of a line segment.
A line and a segment
As two points can fix a segment, it is also true for lines. There exists a unique line that
passes through two given distinct points. Since line is a type of curve, we are
interested in finding out the equation of a line.
Equation of a line
Two-point form
It is given two points A and B and a line passes through them. We may assume there is
an arbitrary point P lies on the line. Then P must satisfy the followings:
The slope of segment AP is the same as that of AB.
P is a point of division of segment AB.
We will find the equation of a line using the first condition. Readers may try the
second condition.
Example 13a: Given two points A (x1, y1) and B (x2, y2). Find the equation of the line
passing though them.
Solution 13a:
Let P (x, y) be an arbitrary point lies on the line. Then slope of AP is equal to slope of
AB. Thus:
y − y1 y2 − y1
=
(13.1)
x − x1 x2 − x1
This equation holds for all P on the line. Thus (13.1) is the equation for the line
passing through A and B.
(13.1) is known as the two-point form of a line.
Example 13b: Find the equation of the line joining (5, -1) and (2, 7).
118
Mathematics Competition Training Class Notes
Coordinates Geometry
Solution 13b:
The equation of the line is:
y − 7 −1 − 7
=
x−2 5−2
3 ( y − 7 ) = −8 ( x − 2 )
(13.2)
8 x + 3 y − 37 = 0
y
(2, 7)
8x + 3y – 37 = 0
5
x
0
5
(5, -1)
Point-slope form
Besides determining a line by two points, one can also find it out by its slope and a
point on it. Using a similar approach in example 13a, if the point is (x1, y1) and the
slope is m, then the equation is:
y − y1
=m
(13.3)
x − x1
Or:
y – y1 = m (x – x1)
(13.4)
(13.4) is known as the point-slope form of a line.
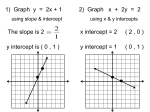
Slope-intercept form
An intercept of a curve is a point that cut the axis. If the axis is an x-axis, the
intercept is called an x-intercept; if the axis is y-axis, it is called a y-intercept. For
example, the x-intercept of the line in example 13b is 37⁄8 and the y-intercept is 37⁄3.
If the y-intercept and slope of a line is given, we can determine that line. It is because
the y-intercept is just a point and we can use the point-slope form to find out the
equation of the line. If the y-intercept is c and the slope is m, then the equation is:
119
Mathematics Competition Training Class Notes
Coordinates Geometry
y = mx + c
(13.5)
This is the slope-intercept form of a line.
Intercept form
If we are given the two intercepts of the line, we can also tell the equation the line
using two-point form. If the x-intercept is b and y-intercept is c, then:
x y
+ =1
b c
(13.6)
This is known as the intercept form of a line.
General form
Recall that we define a curve as set of points satisfying f(x, y) = 0. If we can arrange
the equation for a curve in the form “= 0”, then we say that is the general form of the
curve. For a line, its general form is:
Ax + By + C = 0
(13.7)
For real numbers A, B and C. By rearranging (13.7) into slope-intercept and intercept
form, we have:
C

 x-intercept = − A

C

 y -intercept = −
B

A

Slope = −

B

(13.8)
Distance between point and line*
The distance between a point (x0, y0) and a line L: Ax + By + C = 0 can be given by:
Ax + By0 + C
d =± 0
(13.9)
A2 + B 2
The sign is taken opposite to that of C. If the point and the origin are lying on the
same side of L, the distance is negative. Otherwise, it is positive. Usually we just use
the absolute value of (13.9) in practical use.
120
Mathematics Competition Training Class Notes
Coordinates Geometry
Intersecting Lines
Intersection of two lines
When there are two lines in a coordinates system, we may ask, “where will they
intersect?” This will be introduced here.
Assume we have two lines L1: ax + by + c = 0 and L2: dx + ey + f = 0. If P (x0, y0) is
the intersection of L1 and L2 then this should satisfy both equations L1 and L2, i.e.,
 ax0 + by0 + c = 0

dx0 + ey0 + f = 0
(14.1)
This is just a set of ordinary simultaneous linear equations in 2 unknowns. Using the
notation in set theory we may write P = L1 ∩ L2.
Example 14a: Find
Area of red triangle
in the following figure, if AM : MB =
Area of rectangle
CN : DN = 1 : 2 and BP = CP.
A
M
B
I
P
J
D
N
C
Solution 14a:
Without loss of generality assume the figures lies on a coordinates system with origin
at D and A = (0, 2) and C = (3, 0). It is because ratio is invariant in scaling. Therefore
B = (3, 2), P = (3, 1), M = (1, 2) and N = (2, 0). Thus:
DP : x = 3 y
(14.2)
DM : y = 2 x
AN : x + y = 2
2 4
3 1
Thus I = DM ∩ AN =  ,  and J = DP ∩ AN =  ,  . So the area of the red
3 3
2 2
0
0
132 12 5
5
triangle is
= . But the area of the rectangle is 6. Thus the answer is .
223 43 6
36
0
0
121
Mathematics Competition Training Class Notes
Coordinates Geometry
Angle between two lines
We are also interested in finding the angle formed between two lines. But we need a
lemma:
Another representation of slope
P
x
θ
X
R
Using the definition of slope and the above figure, we know that the slope =
from definition of trigonometric function we know
PR
. But
XR
PR
= tan θ . Hence we have:
XR
(14.3)
Slope = tan θ
The value θ is known as the inclination of the line, which is the angle between the
line and the x-axis.
Angle between two lines
Refer to the following figure,
L2
L1
θ
β1
β2
X2
X1
It is easy to show that β2 – β1 = θ. If the slope of L1 is m1 and L2 is m2, then:
122
Mathematics Competition Training Class Notes
Coordinates Geometry
tan θ = tan ( β1 − β2 )
=
tan β1 − tan β2
1 + tan β1 tan β2
=
m1 − m2
1 + m1m2
(14.4)
However, the last value may be negative. If we are only concentrated to the acute
angle between the two lines, we can takes its absolute value, i.e.,
tan θ =
m1 − m2
1 + m1m2
(14.5)
When two lines parallel, the angle between is 0°. Thus from (14.5),
(L1 // L2) ⇔ (m1 = m2)
(14.6)
When two lines are perpendicular to each other, i.e., the angle between them is 90°,
the denominator of its tangent is zero. Thus:
(L1 ⊥ L2) ⇔ (m1m2 = –1)
(14.6)
Example 14b: (HKCEE 1997/A) L is the line y = 2x + 3. A line with slope m makes
an angle of 45° with L. Find the value(s) of m.
Solution 14b:
The slope of L is 2. From (14.4),
tan 45° =
(1) 1 + 2m
m−2
1 + 2m
= m−2
1 + 2m = m − 2
m = −3
or
1 + 2m = 2 − m
or
m=
123
1
3
(14.7)
Mathematics Competition Training Class Notes
Coordinates Geometry
Locus and Parametric Equation
Locus
In mathematics, locus is a curve traced out by a moving point. This point usually
satisfies some conditions we want. To find out the equation of a locus, we usually let
the point be (x, y) and join the other conditions to make up an equation in terms of x
and y.
Example 15a: Find the locus of a point P such that the distant between P and (2, 5) is
always 3.
Solution 15a:
Let P = (x, y). Hence:
( x − 2)
2
+ ( y − 3) = 3
2
x2 − 4 x + 4 + y 2 − 6 y + 9 = 9
(15.1)
x + y − 4x − 6 y + 4 = 0
2
2
Is the required locus.
Example 15b: Given two curves H: x2 – y2 = 1 and C: x2 + y2 = 4. X is an intersection
of C and H in the first quadrant. Let P be a point on C such that the line XP intersects
H at Q. Find the locus of the midpoint of PQ.
Solution 15b:
y
2
M
Q
P
X
x
-4
-2
0
2
4
H
-2
C
Locus of M
This figure shows a brief look of the graph. Here we let M to be the midpoint of PQ.
124
Mathematics Competition Training Class Notes
Coordinates Geometry
Since we are going to find the locus of M, we let M = (x, y). For P, Q and X, we let
them to be (a, b), (c, d) and (m, n). Since X is an intersection of H and C, we have:
 m2 − n2 = 1
 2
2
m + n = 4

m, n > 0

(15.2)
5
3
and n =
. If we let the equation of XP to be y – n = k (x – m) for
2
2
some constant k denoting the slope, then:
Thus m =
ka − b + ( n − km ) = 0

a2 + b2 = 4

(15.3)
kc − d + ( n − km ) = 0

c2 − d 2 = 1

(15.4)
And:
Solving (15.3) gives a =
gives c =
5 ( k 2 − 1) − 2 3k
5 ( k 2 + 1) − 2 3k
2 ( k − 1)
2
2 ( k 2 + 1)
,d =
,b=
− 3 ( k 2 − 1) − 2 5
− 3 ( k 2 + 1) + 2 5k
2 ( k − 1)
2
2 ( k 2 + 1)
. Since x =
. Solving (15.4)
a+c
b+d
,y=
,
2
2
we have:
x=
y=
5 ( k 4 + 1) − 2 3k 3
2 ( k 4 − 1)
− 3 ( k 4 + 1) + 2 5k
(15.5)
2 ( k 4 − 1)
This is a parametric equation, which will be introduced in this section:
Parametric equation
 x = f ( t )
Parametric equations are equations describing a curve in the form 
or
 y = g ( t )
(f(t), g(t)). Here f and g are real-valued functions and t is a real variable, called the
parameter of the curve. As t changes, the point (f(t), g(t)) moves. If we find the locus
of this point the result will be a curve this parametric equation describing.
125
Mathematics Competition Training Class Notes
Coordinates Geometry
Example 15c: Sketch the graph with x = t + 5, y = 5t – 1 for t ∈ [-3, 3].
Solution 15c:
We can plot a few points with respect to t then join them up to get a rough image of
the graph.
y
t=3
10
t=2
t=1
x
t = 1/2
0
2
4
6
8
t=0
t = -1
-10
t = -2
t = -3
The curve is a segment.
Converting general equation into parametric equation*
If the curve is of the form y = f(x), then we can just set x = t and y = f(t) to form a
parametric equation. If the curve is f(x, y) = 0, then we may (I) convert it into the form
y = g(t) or (II) find two functions h1(t) and h2(t) such that f(h1(t), h2(t)) = 0. Then
x = h1(t) and y = h2(t).
Example 15d: Convert the curve x2 + y2 = 1 into parametric form.
Solution 15d: Since sin2 t + cos2 t = 1 for all t, the parametric form is (sin t, cos t).
Converting parametric equation into general equation
To convert a parametric equation into its general form, the only way is to eliminate
the parameter and connect x and y in one equation. To eliminate the parameter one can
(I) express t in terms of x or y then substitutes this into the other equation, or (II) find
a function such that f(x(t), y(t)) = constant.
t 

Example 15e: Convert  t + 2,
 into general form.
t−2

126
Mathematics Competition Training Class Notes
Coordinates Geometry
Solution 15e:
Let x = t + 2 and y =
t
.
t−2
Method (I):
Hence t = x – 2. Substitute this into y gives:
y=
x−2
x−4
(15.6)
That means xy – x – 4y + 2 = 0 is the general form.
Method (II):
First of all, notice that
x t2 − 4
=
, which is simpler in expressing. If we subtract
y
t
2 2t − 4
x − 2 t 2 − 2t
=
from it, the result will be
=
= t − 2 . Subtract x again from it
y
t
y
t
gives
x−2
− x = −4 . Rearranging this also result in xy – x – 4y + 2 = 0.
y
127
Mathematics Competition Training Class Notes
Coordinates Geometry
Circles
What are circles?
In coordinates geometry, circles are loci of a point P that is equidistant from another
point O. The point O is called the center of the circle and the length OP is the radius.
If the center of the circle is (x0, y0) and the radius is r, then the equation of the circle
is:
(x – x0)2 + (y – y0)2 = r2
(16.1)
This is called the standard form of the circle. We can expand (16.1) into:
x2 + y2 – 2x0 x – 2y0 y + (x02 + y02 – r2) = 0
(16.2)
To get its general form. If it is given the general form of a circle to be:
x2 + y2 + ax + by + c = 0
(16.3)
Then:
b

 a
Center =  − 2 , − 2 



(16.4)

a 2 + b 2 − 4c

Radius =
2
2
2
So, when a + b – 4c = 0, the “circle” reduced into a point. This is called a point
circle. When a2 + b2 – 4c < 0, the radius will be unreal and no graph can be drawn.
Then that equation is said to be representing an imaginary circle.
Example 16a: Given a triangle ∆ABC such that the vertices A, B, C are (2, 5), (1, 7)
and (-4, 2) respectively. Find:
The equation of the circumcircle Γ of ∆ABC, and
The intersection (other than A) of Γ and the altitude of ∆ABC from A.
Solution 16a:
The first question means to find a circle Γ such that A, B, C all lies on it. We let Γ to
be x2 + y2 + ax + by + c = 0. So:
 22 + 52 + 2a + 5b + c = 0

12 + 7 2 + a + 7b + c = 0


2
2
( −5 ) + 2 − 5a + 2b + c = 0
Solving this gives Γ: x2 + y2 + 3x – 9y + 10 = 0.
128
(16.5)
Mathematics Competition Training Class Notes
Coordinates Geometry
For the second equation, let the altitude be L. Therefore, L ⊥ BC. Since the slope of
BC is 1, the slope of L is –1. By point-slope form, the equation of L is x + y – 7 = 0.
Thus the intersection satisfies:
x+ y−7 = 0

 2
2
 x + y + 3x − 9 y + 10 = 0
(16.6)
Hence the intersection is (-1, 8). (The other solution (2, 5) should be rejected because
it is just the point A.)
8
L
7
Γ
B
6
A
5
4
3
2
C
1
-6
-4
-2
2
4
Tangent of circle
If a curve C intersects a curve C’ at exactly one point somewhere and C’ does not
appear on both sides separated by C there, C and C’ are tangent to each other. This is
especially important if C is a line; this will be called the tangent of C’. In this section
we will show how to find the tangent of a circle.
Tangent of circle passing through a point on circle
Let C: x2 + y2 + ax + by + c be a circle with center O and T (x0, y0) be
a point on the C such that a tangent L passes through it. Thus OT ⊥ L.
y + b 2 2 y0 + b
=
, the slope of L is
Since slope of OT is 0
x0 + a 2 2 x0 + a
−
2 x0 + a
. Therefore, by point-slope form, the equation of L is:
2 y0 + b
129
C
L
O
T
Mathematics Competition Training Class Notes
Coordinates Geometry
 2x + a 
y − y0 =  − 0
 ( x − x0 )
 2 y0 + b 
(16.7)
ax + by + 2 x0 x + 2 y0 y − ax0 − by0 − 2 ( x02 + y02 ) = 0
But because T is on C, we have:
x02 + y02 = − ax0 − by0 − c
(16.8)
Substitute this back to (16.7) and simplifying gives:
x +x
 y + y
+ b 0
L : x0 x + y0 y + a  0

+c =0
 2 
 2 
(16.9)
Example 16b: Using the figure in example 16a, let the LA, LB and LC be the three
tangents of Γ passing through A, B and C respectively. Find the length of the segment
connecting LA ∩ LB and LA ∩ LC.
Solution 16b:
The tangent through A (LA) is:
LA : 2 x + 5 y +
3
2
( x + 2 ) − 92 ( y + 5) + 10 = 0
(16.10)
: 7 x + y − 19 = 0
Similarly, the LB is x + y – 8 = 0 and LC is x + y + 2 = 0. Thus the two intersections are
25 2
 7 11 
 11 37 
.
 , −  and  ,  and the distance is
3
2 2 
6 6 
Lengths of tangent from external point
If a point is outside a circle and tangents passes through it, there will
be exactly two tangents. Nevertheless, their lengths (XT and XU in
the figure) are the same. We wish to find the value of this. If the
circle is (x – ζ)2 + (y – η)2 = r2 and X = (x0, y0), then by Pythagoras’
theorem, XT2 + r2 = OX2. But OX2 = (x0 – ζ)2 + (y0 – η)2. So:
XT =
( x0 − ζ )
2
+ ( y0 − η ) − r 2
2
T
X
O
U
(16.11)
But this is just the value of the equation of the circle when (x, y) = (x0, y0). Hence, if
the circle in general form is x2 + y2 + ax + by + c = 0, the length of tangent is:
x02 + y02 + ax0 + by0 + c
(16.12)
Many circles
If we are given two circles on a coordinates system, we can tell their relationship by
the distance of their centers and their radii. If the radii of the two circles are r1 and r2
130
Mathematics Competition Training Class Notes
Coordinates Geometry
respectively with r1 > r2, then:
Distance of centers in…
Implication
(r1 + r2, ∞)
Two circles separates
{r1 + r2}
They are tangent to
each other externally
(r1 – r2, r1 + r2)
They intersect at 2 points
{r1 – r2}
They are tangent to
each other internally
[0, r1 – r2)
One circle is inside
the other
If the two circles intersect, there will be a common chord which passes through the
two intersections. If they are C1: x2 + y2 + a1x + b1y + c1 = 0 and
C2: x2 + y2 + a2x + b2y + c2 = 0, simple calculation suggests that the equation of the
common chord is:
L: (a1 – a2) x + (b1 – b2) y + (c1 – c2)
(16.13)
Or an easy-to-remember representation:
L: C1 – C2
(16.14)
If C1 and C2 are tangent to each other, then L reduced to one of the common tangents
of them.
Example 16c: Prove that the common chords of any three intersecting circles are
always concurrent.
Solution 16c:
Let the three circles be C1: x2 + y2 + a1x + b1y + c1 = 0, C2: x2 + y2 + a2x + b2y + c2 = 0
and C3: x2 + y2 + a3x + b3y + c3 = 0. Thus the three chords are
L3: (a1 – a2) x + (b1 – b2) y + (c1 – c2) = 0, L1: (a2 – a3) x + (b2 – b3) y + (c2 – c3) = 0
and L2: (a3 – a1) x + (b3 – b1) y + (c3 – c1) = 0. Let the intersection of L3 and L1 be X.
Since X satisfy both L1 and L3, it would also satisfy:
L1 + L3: (a1 – a3) x + (b1 – b3) y + (c1 – c3) = 0
(16.15)
But this is just L2. Therefore, X is on L1, L2 and L3. That means the three chords are
concurrent.
Q.E.D.
131
Mathematics Competition Training Class Notes
Coordinates Geometry
Parabola
The quadratic polynomial in coordinates geometry
If we graph the curve y = x2 on a coordinates system, the result would be something
like this:
This curve is called a parabola. In physics, the (upside-down) parabola resembles the
path of an object thrown at an angle, and it is why this curve named like this (it means
“to throw across” in Greek).
In mathematics, a parabola is the curve y = ax2 + bx + c for a ≠ 0. The following
shows some example of parabolas:
y
4
2
x
-4
-2
0
-2
132
2
4
Mathematics Competition Training Class Notes
Coordinates Geometry
Some properties associated to parabola
x-Intercepts
In Elementary Algebra, we learnt that the discriminant ∆ = b2 – 4ac determines how
many real roots a does a quadratic equation has. In coordinates geometry, the root of a
curve is same as its x-intercept. Therefore, ∆ decides how the parabola will cross the
x-axis. The x-intercepts would be the roots of the quadratic polynomial.
y
4
2
x
-2
0
2
4
Three parabolas with different values of ∆.
The purple one: ∆ < 0. The yellow one: ∆ = 0. The blue one: ∆ > 0.
y-Intercept
A function will cross the y-axis when x = 0. By substituting this, we know that the
y-intercept of a parabola is the constant term of its equation, i.e., c.
y
x
0
5
10
-5
-10
The parabola y = ½ x2 – 5x + 1. The y-intercept is 1 according to the graph.
133
Mathematics Competition Training Class Notes
Coordinates Geometry
Extremum and direction of opening
An extremum means the maximum or minimum point of a function. By completing
the square, a quadratic polynomial can be expressed as:
a (x – h)2 + k
Where h = −
(17.1)
b
∆
,k = −
. Because n2 ≥ 0 for any real number n, the maximum /
2a
4a
minimum of (17.1) will be k depending on the sign of a. The value k can be achieved
when x = h. Thus, (h, k) is the extremum of a parabola.
y
(0.5, -2.75)
-5
-10
(5, -11.5)
0
5
10
Two parabolas: y = -x2 + x – 3 and y = ½ x2 – 5x + 1.
The extremum will be a minimum when a > 0 (Why?). It will be a maximum when
a < 0. If the extremum of a parabola is a minimum, then no points can lower than this
point. Thus the parabola opens upwards. Similarly, if the extremum is a maximum, the
parabola opens downwards. That means when a is positive, the parabola opens
upwards. When a is negative, the parabola opens downwards.
In some books the point “extremum” is called the “vertex” of a parabola.
Example 17a: (HKCEE 1990/2) The graph of y = ax2 + bx + c is given as shown.
Which of the following is/are negative: a, b or c?
y
x
O
134
Mathematics Competition Training Class Notes
Coordinates Geometry
Solution 17a:
From the graph, the y-intercept is negative. Thus c is negative. Also, the parabola
opens downward, thus a is also negative. The sum of roots is positive, thus −
This means b is positive. Therefore, a and c are negative.
135
b
> 0.
a
Mathematics Competition Training Class Notes
Coordinates Geometry
Coordinates Geometric Transformation
What is transformation?
In reality, if you have an object, you can move it, rotate it, squeeze it, pull it, destroy it,
etc. These are transformations of the object. Transformation of something means to
change the shape and/or position of something in a specific way. In coordinates
geometry, a transformation can be represented by a function τ: R2 → R2. This function
maps a point to a different (or same) coordinates. Since a curve is composed of points,
if we transform every point on the original curve, the result will be another curve
transformed by τ. Usually if we transform a curve C by τ, we simply write τ(C), which
actually means the set {τ(x) | x ∈ C}.
Translation
Translation is a transformation. This transformation will move every point by a fixed
distance and direction. If the origin is mapped to (a, b), then the transformation is
given by:
T(x, y) = (x + a, y + b)
(18.1)
If the original curve it C: f(x, y) = 0, the translated curve will be f(x – a, y – b) = 0. We
say the curve is translated by (a, b).
y
2
x
-2
0
2
4
6
-2
The curve x2 + y2 = 4 is translated by (5, 1).
Scaling
Scaling, also called homothety, is a transformation that makes an object bigger or
smaller. To demonstrate the mechanism, imagine you want to take a picture of
something far away using a digital camera. This thing looks too small in preview. To
have a clear look of this thing, you would zoom in. During zooming, the objects
around the thing are getting farther away (in the picture!), and the result would be the
136
Mathematics Competition Training Class Notes
Coordinates Geometry
whole view getting larger and larger.
This is exactly how scaling works. One point is fixed during scaling, and the other
will move away from / towards that point. The points that are farther apart from the
fixed point are moving “faster”. If the fixed point is (a, b), and a line segment of
length 1 is scaled up / down to length r, than the transformation function is:
H(x, y) = (r (x – a) + a, r (x – b) + b)
(18.2)
Usually the fixed point is taken to be the origin. Hence:
H0(x, y) = (rx, ry)
(18.3)
If a curve C: f(x, y) = 0 is transformed by H, the new curve will be
y+b
x+a

− a,
− b  = 0 . The curve C is said to be scaled by a factor of r around
f
r
 r

(a, b).
y
2
x
-2
0
2
4
-2
-4
The curve x2 + y2 = 4 is scaled by a factor of 2 around (-1, 1).
If the factor is greater than 1, the figure is enlarged. If the factor is in between 0 and 1,
the figure is shrunk. If the factor is negative, the figure is inverted.
Reflection
If you look at a mirror, you would find yourself behind the mirror with the direction
inverted. This is a kind of reflection. In geometry, reflection is a transformation that
maps every point P to another point P’ with respect to a line L such that the distance
between P’ and L is same as that of P and L and PP’ is perpendicular to L.
137
Mathematics Competition Training Class Notes
Coordinates Geometry
Example 18a: Find the function of reflection if L is Ax + By + C = 0.
Solution 18a:
Let P = (x, y), P’ = (x’, y’) and the function be S: R2 → R2. Therefore:
S(x, y) = (x’, y’)
(18.4)
B
. That means:
A
Since PP’ is perpendicular to L, the slope of PP’ is
y − y′ B
= .
x − x′ A
(18.5)
Now because the distance from P and P’ to L are the same, and P and P’ are on
opposite sides of L (otherwise P = P’, and this is not a reflection), we have:
Ax + By + C = –Ax’ – By’ – C
(18.6)
Using (13.9). Solving (18.5) and (18.6) for x’ and y’ gives:
 ( B 2 − A2 ) x − 2 A ( C + By )
S ( x, y ) = 
,

A2 + B 2

If
a
curve
f(x,
y)
=
0
is
(A
2
− B 2 ) y − 2 B ( C + Ax ) 


A2 + B 2

transformed
by
S,
the
new
(18.7)
curve
is
 ( B 2 − A2 ) x + 2 A ( C + By ) ( A2 − B 2 ) y + 2 B ( C + Ax ) 

 = 0 . We say the curve is
,
f


A2 + B 2
A2 + B 2


reflected along L.
y
5
x
-10
-5
0
-5
The curve y = x2 is reflected along x + 2y + 3 = 0.
The resulting curve is 9x2 – 24xy + 16y2 – 16x + 63y + 96 = 0.
138
Mathematics Competition Training Class Notes
Coordinates Geometry
The formula (18.7) is extremely hard to memorized, so we recommend readers do not
use this if possible.
Rotation*
Rotation is a transformation that moves a point P to another point P’ around a fixed
point O such that ∠POP’ is constant. If this angle is α, we say that P is
rotated by an angle of α about O. However, there may be two
choices of P’, as shown on the right. In mathematics, we
usually measure angle in counterclockwise direction.
O
Therefore, if α is positive, we take the blue P’. If we want the
red one, make α negative.
P’
P
P’
In coordinates geometry, rotation is evaluated as:
R(x, y) = (cos α (x – a) – sin α (y – b) + a, sin α (x – a) + cos α (y – b) + b) (18.8)
Where (a, b) is the center of rotation (the point O) and α is the angle. A curve is
transformed as:
f ( cos α ( x − a ) + sin α ( y − b ) + a, − sin α ( x − a ) + cos α ( y − b ) + b ) = 0 (18.9)
y
6
4
2
-4
-2
0
x2
The curve y = x2 is rotated about (0, -1) by 45°.
Invariants in transformations*
In the transformations listed above, some quantities are not changed. These are the
invariants of that transformation. The table below shows some invariants:
139
Mathematics Competition Training Class Notes
Invariants
Coordinates Geometry
Translation Scaling Reflection Rotation
Length and area
Ratio
Angle between two lines
Slope
Type / number of intersections
Coordinates
Points on L
140
Mathematics Competition Training Class Notes
Coordinates Geometry
Summary
Coordinates System
In a coordinates system, a point can be defined by a pair of numbers called
coordinates.
The rectangular coordinates system is created by two perpendicular real
lines, called the x-axis and y-axis respectively, that are crossing at their
zeros.
The coordinates of a point are given by the readings on the axes. They are
denoted as (x, y).
Coordinates system = {(x, y) | x, y ∈ R} = R2.
The axes divide the coordinates system into four quadrants.
II I
III IV
Line Segment
{( x, y ) ∈ ℝ
}
f ( x, y ) = 0 , where f: R2 → R.
Curves are defined as C =
Usually C is just written as “f(x, y) = 0”.
Line segments are of curve that is not “curved” at all, and length is finite.
If a segment connects (x1, y1) and (x2, y2), then:
Length =
Slope =
( x1 − x2 )
2
+ ( y1 − y2 )
2
2
y1 − y2
x1 − x2
 rx + sx1 ry2 + sy1 
,
divides the segment into ratio r : s
The point  2
r + s 
 r+s
internally.
A negative ratio of division means the point divides the segment
externally.
x1
1 x2
Area of triangle =
2 x3
x1
x1
y1
x2
y2
1
. Area of polygon = ⋮
y3
2
xn
y1
x1
141
y1
y2
⋮ .
yn
y1
Mathematics Competition Training Class Notes
Coordinates Geometry
Lines
Lines are curves that are straight and infinite in length.
There exists a unique line that passes through any two distinct points.
y − y1 y2 − y1
=
Two-point form of a line:
x − x1 x2 − x1
Point-slope form: y – y1 = m (x – x1).
Slope-intercept form: y = mx + c
Intercept form:
C

 x-intercept = − A

C

General form of a line: Ax + By + C = 0, where  y -intercept = − .
B

A

Slope = −

B

*
x y
+ =1.
b c
Distance between a point and a line is d = ±
Ax0 + By0 + C
A2 + B 2
, where the sign
is taken opposite to that of C.
Intersecting Lines
Finding intersection P of two lines L1, L2 is same as finding solution to a set
of simultaneous linear equations in 2 unknowns. We write P = L1 ∩ L2.
Slope = tan θ, where θ is the inclination of a line, which is the angle
between it and the x-axis.
Angle between two lines: tan θ =
m1 − m2
.
1 + m1 m2
(L1 // L2) ⇔ (m1 = m2)
(L1 ⊥ L2) ⇔ (m1m2 = –1)
Locus and Parametric Equation
Locus is a curve traced out by a moving point.
We let the moving point be (x, y) to make up the equation of locus.
Parametric equations are equations describing a curve in the form (f(t), g(t)).
Circles
Circles are loci of a point that is equidistant from another point.
142
Mathematics Competition Training Class Notes
Coordinates Geometry
If the center is (x0, y0) and the radius is r, then the circle is
(x – x0)2 + (y – y0)2 = r2. This is the standard form of a circle.
General form of circle: x2 + y2 + ax + by + c = 0, where
b

 a
Center =  − 2 , − 2 



.

a 2 + b 2 − 4c

Radius =
2
If a curve C intersects a curve C’ at exactly one point somewhere and C’
does not appear on both sides separated by C there, C and C’ are tangent to
each other.
The tangent line of x2 + y2 + ax + by + c = 0 at (x0, y0) is
x +x
 y + y
+ b 0
x0 x + y0 y + a  0

+c =0.
 2 
 2 
Length of the tangent from an external point (x0, y0) is
x02 + y02 + ax0 + by0 + c .
Relationship of two circles:
Distance of centers in…
Implication
(r1 + r2, ∞)
{r1 + r2}
(r1 – r2, r1 + r2)
{r1 – r2}
[0, r1 – r2)
Common chord/tangent of two circles: L: C1 – C2.
Parabola
Parabola is the curve y = ax2 + bx + c for a ≠ 0.
x-intercepts of parabola are roots of that quadratic polynomial.
∆ decides how the parabola will cross the x-axis.
y-intercept = c.
∆
 b
Extremum / Vertex =  − , −  .
 2a 4a 
143
Mathematics Competition Training Class Notes
Coordinates Geometry
(a > 0) ⇔ (parabola opens upwards).
(a < 0) ⇔ (parabola opens downwards).
Coordinates Geometric Transformation
Transformation means to change shape and/or position of something.
Translation: T(x, y) = (x + a, y + b)’
Scaling: H(x, y) = (r (x – a) + a, r (x – b) + b)
Reflection:
 ( B 2 − A2 ) x − 2 A ( C + By ) ( A2 − B 2 ) y − 2 B ( C + Ax ) 
.
S ( x, y ) = 
,


A2 + B 2
A2 + B 2


*
*
Rotation:
R(x, y) = (cos α (x – a) – sin α (y – b) + a, sin α (x – a) + cos α (y – b) + b).
Invariants in transformation:
Invariants
Translation Scaling Reflection Rotation
Length and area
Ratio
Angle between two lines
Slope
Type / number of intersections
Coordinates
Points on L
144
Mathematics Competition Training Class Notes
Coordinates Geometry
Self Assessment Exercises
Level 1
1) Solve the followings:
a) Find and express the equation of the line passing through (cos t, sin t) and
(-sin t, cos t) in terms of t.
b) Show that this line is tangent to the circle 2x2 + 2y2 – 1 = 0.
[Hint: Consider the distance from the origin to the line]
2) (HKCEE 1994/2) In the figure, the line y = mx + k cuts the curve y = x2 + bx + c at
x = α and x = β. Find the value of αβ in terms of b, c, m and/or k.
y
y = x2 + bx + c
y = mx + k
x
α
β
3) Prove the length is invariant in translation.
4) (HKMO 1996/HG Q1) In the figure, the quadratic curve y = f(x) cuts the x-axis at
two points (1, 0) and (5, 0) and the y-axis at point (0, -10). Find the value of p.
y
(4, p)
1
5
x
-10
5) (IMSC 2000/FG1 Q1) Let u, v be integers such that 0 < v < u. Let A = (u, v), B be
the reflection of A along the line y = x, C be reflection of B along the y-axis, D be
the reflection of C along the x-axis and E be the reflection of D along the y-axis.
The area of the pentagon ABCDE is 451. Find u + v.
Level 2
6) (JSMQ 1999/FG Q2) A belt fits around three circles x2 + y2 = 1, (x – 14)2 + y2 = 1
and (x – 9)2 + (y – 12)2 = 1. Find the length of the belt.
7) (Apollonian Circle) Let A be (-1, 0) and B be (1, 0). Find the locus of P such that
AP
= r and express it in terms of r. What kind of curve is it?
PB
145
Mathematics Competition Training Class Notes
Coordinates Geometry
8) (PSMSIMC 2004/S Q14c) In the figure, the radius of the circle is 1 and AP is a
diameter of the circle. B is a point on the circumference and C is a point on BP
such that PC : CD = 5 : 3. If M is the mid-point of AC and BM is extended to meet
AP at Q, find the maximum possible area of ∆BPQ.
[Hint: Find the locus of C as B moves and show that Q is a fixed point]
B
C
M
A
P
Q
9) (IMOPHK 2004 Q13) Find the area enclosed by the graph x2 + y2 = |x| + |y| on the
xy-plane.
10) (ISMC 2003/I Q7) A piece of graph is folded once so that (0, 2) is matched with
(4, 0) and (7, 3) is matched with (m, n). Find m + n.
11) In the figure, P is a point on the line y = x – 7. Find the minimum value of
AP + BP and the corresponding coordinates of P.
y=x–7
P
A (5, -3)
B (3, -6)
12) Solve the followings:
a) Find the locus P of point X such that the distance from X to the line
L: y = -¼ and the point F (0, ¼) is the same.
b)
The circle C: x2 + y2 = 1 intersects P and L at four points. Find the area of
the quadrilateral enclosed by these four points.
c)
It is given that if X (x0, y0) is a point on P, the slope of the tangent to P
passing through X is 2x0. Find the common tangent(s) of C and P.
146
Mathematics Competition Training Class Notes
Coordinates Geometry
Answers
1) a) dfdf
4) 6
5) 21
6) 2π + 42
7) x 2 + y 2 −
2 ( r + 1)
r −1
x + 1 = 0 . This is a curve with center on the x-axis.
8) 8⁄11
9) π + 2
10) 6.8
11) 17; P = ( 113 , − 103 )
12) a) y = x2. b)
(2
)(
5 −1
15 + 2 2 5 − 2
16
147
) . c) y = ±2x
2+ 5 −2− 5 .
Mathematics Competition Training Class Notes
Coordinates Geometry
Chinese Translation of Important Terms
Abscissa
橫坐標
Altitude
垂線
Center
圓心
Circle
圓
Circumcircle
外接圓
Collinear
共線
Common chord
公共弦
Common tangent
公切線
Concurrent
共點
Coordinates
坐標
Coordinates system
坐標系統
Curve
曲線
Equidistant
同距
External point of division
外分點
Extremum
極值
General form
一般式
Homothety
位似變換
Hypotenuse
斜邊
Imaginary circle
虛圓
Inclination
傾角
Intercept
截距
Intercept form
截距式
Internal point of division
內分點
Invariant
不變量
Line segment
線段
Locus (pl. loci)
軌跡
Midpoint formula
中點公式
Ordinate
縱坐標
Origin
原點
Parabola
抛物線
Parameter
參數
Parametric equation
參數方程
Point circle
點圓
Point of division
分點
Point-slope form
點斜式
148
Mathematics Competition Training Class Notes
Coordinates Geometry
Polygon
多邊形
Project
投影
Pythagoras’ theorem
畢氏定理
Quadrant
象限
Quadrilateral
四邊形
Radius (pl. radii)
半徑
Ray
射線
Rectangular coordinates system 直角坐標系統
反射
Reflection
Right triangle
直角三角形
Rotation
旋轉
Scaling
縮放
Section formula
截點公式
Slope
斜率
Slope-intercept form
斜截式
Standard form
標準式
Tangent
相切、切線
Transformation
變換
Translation
平移
Two-point form
兩點式
Vertex (pl. vertices)
頂點
x-axis
x軸
x-coordinate
x 坐標
x-intercept
x 軸截距
y-axis
y軸
y-coordinate
y 坐標
y-intercept
y 軸截距
149
Mathematics Competition Training Class Notes
Coordinates Geometry
References:
Wikipedia, the free encyclopedia. [http://en.wikipedia.org/]
MathWorld – A Wolfram Web Resource. [http://mathworld.wolfram.com/]
Mathematics Database. [http://www.mathdb.org/]
MathsWorld-2001 [http://mathsworld.ath.cx/]
Original documents:
Coordinates System: Chapter 0 “Before You Start” Section 2; Chapter 2
“Linear Equations” Section 1; Chapter 8 “Trigonometry” Section 5.
Line Segment: Chapter 2 “Linear Equations” Section 1, 5, 7 and 8.
Lines: Chapter 2 “Linear Equations” Section 2 and 5.
Intersecting Lines: Chapter 2: “Linear Equations” Section 3 and 6; Chapter 8
“Trigonometry” Section 12.
Locus and Parametric Equation: Chapter 13: “Parametric Equation and
Locus” Section 1, 2 and 3.
Circles: Chapter 14: “Quadratic Curve” Section 10.
Parabola: Chapter 3: “Quadratic Equation and Polynomial Factorization”
Section 8.
Coordinates Geometric Transformation: Chapter 14: “Quadratic Curve”
Section 9.
150