Lengths of simple loops on surfaces with hyperbolic metrics Geometry & Topology G
... pairing function using the Fenchel–Nielsen coordinates on Teichmüller space and the Dehn–Thurston coordinates on the space of homotopy classes of curve systems. Our main result, theorem 1.1, establishes Lipschitz type estimates for the length pairing expressed in terms of these coordinates. As a co ...
... pairing function using the Fenchel–Nielsen coordinates on Teichmüller space and the Dehn–Thurston coordinates on the space of homotopy classes of curve systems. Our main result, theorem 1.1, establishes Lipschitz type estimates for the length pairing expressed in terms of these coordinates. As a co ...
Solution Guide for Chapter 6: The Geometry of Right Triangles
... From this figure we read a value of a = 1.73. It turns out that the second crossing point occurs at a = 11.57. Both of these values of a produce a triangle with a perimeter of 25 units. (d) We want to find when the graph we have made reaches a minimum. This is shown in the figure on the right above, ...
... From this figure we read a value of a = 1.73. It turns out that the second crossing point occurs at a = 11.57. Both of these values of a produce a triangle with a perimeter of 25 units. (d) We want to find when the graph we have made reaches a minimum. This is shown in the figure on the right above, ...
2. 1.2. Exercises
... 2. 10.2. Tangential and cyclic quadrilaterals ............................................................... 102 3. 10.3. The area of circles ........................................................................................... 103 11. Exercises ............................................... ...
... 2. 10.2. Tangential and cyclic quadrilaterals ............................................................... 102 3. 10.3. The area of circles ........................................................................................... 103 11. Exercises ............................................... ...
Test - FloridaMAO
... Consecutive angles are supplementary. Same side exterior angles are congruent. Alternate interior angles are supplementary. Vertical angles are congruent. ...
... Consecutive angles are supplementary. Same side exterior angles are congruent. Alternate interior angles are supplementary. Vertical angles are congruent. ...
kucukarslan et al.
... Fuzzy sets theory was introduced by Zadeh in 1965. A fuzzy set is characterized by a membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical struct ...
... Fuzzy sets theory was introduced by Zadeh in 1965. A fuzzy set is characterized by a membership function which assigns to each object a grade of membership ranging between zero and one. One of the main goals in the fuzzy sets theory is to give fuzzification of different classical mathematical struct ...
Mechanics
... Weight force The mass and weight of a particle are different. The mass of a particle is defined as the amount of substance in the body; mass is a scalar quantity. When an object is placed on a set of bathroom scales, the reading is the amount of mass in the object, typically in kilograms. When an ob ...
... Weight force The mass and weight of a particle are different. The mass of a particle is defined as the amount of substance in the body; mass is a scalar quantity. When an object is placed on a set of bathroom scales, the reading is the amount of mass in the object, typically in kilograms. When an ob ...
MA352_Differential_Geometry_CIIT_VU
... There are many examples of vector field around us, for example, the gravitational field etc. In such vector fields each point of the domain space represents a vector, for example, in case of gravitation vector field each point of the space represents a vector, directed towards the center of the eart ...
... There are many examples of vector field around us, for example, the gravitational field etc. In such vector fields each point of the domain space represents a vector, for example, in case of gravitation vector field each point of the space represents a vector, directed towards the center of the eart ...
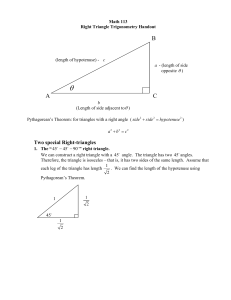
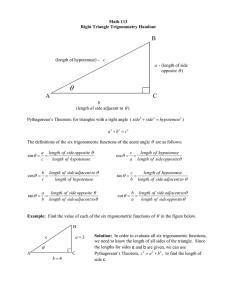
Right Triangle Trig
... they are “similar”. This means that the triangles have the same shape and the lengths of the corresponding sides are in the same ratio. Because an acute angle in a right triangle always gives the same ratio of opposite to adjacent sides, the trigonometric functions’ values evaluated for the angle θ ...
... they are “similar”. This means that the triangles have the same shape and the lengths of the corresponding sides are in the same ratio. Because an acute angle in a right triangle always gives the same ratio of opposite to adjacent sides, the trigonometric functions’ values evaluated for the angle θ ...
Chapter 5
... 31. Write each equation in slope-intercept form. 3x + 5y = -7 -3x - 5y = -7 5y = -3x - 7 -5y = 3x - 7 ...
... 31. Write each equation in slope-intercept form. 3x + 5y = -7 -3x - 5y = -7 5y = -3x - 7 -5y = 3x - 7 ...
Use substitution to solve each system of equations. 1. y = x + 5 3x +
... women will be the same if the current trend continues. Booker is buying tickets online for a concert. He finds tickets for himself and his friends for $65 each plus a one-time fee of $10. Paula is looking for tickets to the same concert. She finds them at another Web site for $69 and a one-time fee ...
... women will be the same if the current trend continues. Booker is buying tickets online for a concert. He finds tickets for himself and his friends for $65 each plus a one-time fee of $10. Paula is looking for tickets to the same concert. She finds them at another Web site for $69 and a one-time fee ...
θ θ θ θ θ θ θ θ θ θ θ θ θ θ θ
... to adjacent sides, the trigonometric functions’ values evaluated for the angle θ will be the same for all of these triangles. Since we know that the size of the triangle is not important, it is helpful to look at right triangles in which the length of the hypotenuse is equal to 1. Here are our 2 spe ...
... to adjacent sides, the trigonometric functions’ values evaluated for the angle θ will be the same for all of these triangles. Since we know that the size of the triangle is not important, it is helpful to look at right triangles in which the length of the hypotenuse is equal to 1. Here are our 2 spe ...
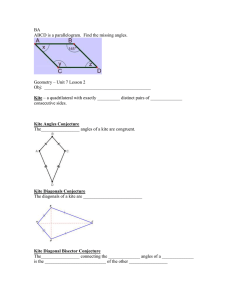
Unit 7 Lesson 2 - Trimble County Schools
... Midsegment – the segment connecting the _________________ of two nonparallel sides of a _____________ ______ ____________________ Three Midsegments Conjecture The three ________________ of a triangle divide it into __________ congruent triangles. ...
... Midsegment – the segment connecting the _________________ of two nonparallel sides of a _____________ ______ ____________________ Three Midsegments Conjecture The three ________________ of a triangle divide it into __________ congruent triangles. ...
lengths of geodesics on riemann surfaces with boundary
... surface. In [8], S. Kerckhoff proves the following theorem. Theorem 2.1. The geodesic length function of a simple closed curve δ is convex along earthquake paths. It is strictly convex if δ intersects γ , the simple closed geodesic along which the earthquake was performed. A surface of genus g can a ...
... surface. In [8], S. Kerckhoff proves the following theorem. Theorem 2.1. The geodesic length function of a simple closed curve δ is convex along earthquake paths. It is strictly convex if δ intersects γ , the simple closed geodesic along which the earthquake was performed. A surface of genus g can a ...
FLEXIBLE MACHINE ELEMENTS
... 1. Find exp (f) from belt geometry and friction 2. From belt geometry and speed find Fc 3. From T= 63025Hnom Ks nd/n find the necessary torque 4. From torque T find the necessary (F1)a – F2 =2T/D 5. Find F2 6. From equation 17-(i) find the necessary initial tension, Fi 7. Find the frictional develo ...
... 1. Find exp (f) from belt geometry and friction 2. From belt geometry and speed find Fc 3. From T= 63025Hnom Ks nd/n find the necessary torque 4. From torque T find the necessary (F1)a – F2 =2T/D 5. Find F2 6. From equation 17-(i) find the necessary initial tension, Fi 7. Find the frictional develo ...
Statistics Test
... formal schooling. They recognize shape by its appearance through qualities such as “pointiness.” They may think that a shape is a rectangle because it “looks like a door.” Young children begin describing objects by talking about how they are the same or how they are different. Teachers will then hel ...
... formal schooling. They recognize shape by its appearance through qualities such as “pointiness.” They may think that a shape is a rectangle because it “looks like a door.” Young children begin describing objects by talking about how they are the same or how they are different. Teachers will then hel ...
THE LEBESGUE UNIVERSAL COVERING
... interior of E 0 but it does enter the interior of region C 0 . Case (3) is where the curve does not enter the interior of E 0 or C 0 . Case (1): If a curve of constant width 1 enters the interior of E 0 then it cannot enter the interior of B 0 since all points inside B 0 are at a distance greater th ...
... interior of E 0 but it does enter the interior of region C 0 . Case (3) is where the curve does not enter the interior of E 0 or C 0 . Case (1): If a curve of constant width 1 enters the interior of E 0 then it cannot enter the interior of B 0 since all points inside B 0 are at a distance greater th ...
final exam review pkt - Niskayuna Central Schools
... equations y x 2 5 and y x . Draw a sketch to prove your answer. ...
... equations y x 2 5 and y x . Draw a sketch to prove your answer. ...
SOLVING SYSTEMS BY GRAPHING INTRODUCTION The objective
... No, this equation is not in slope-intercept form. So what can we do to change it to slope-intercept form? We can add three x to each side of the equation to that y is isolated. Let’s do that now. When we add three x to both sides of the equation, what is the equation in slope-intercept form? The equ ...
... No, this equation is not in slope-intercept form. So what can we do to change it to slope-intercept form? We can add three x to each side of the equation to that y is isolated. Let’s do that now. When we add three x to both sides of the equation, what is the equation in slope-intercept form? The equ ...
Solid sweep - CAD CAM Laboratory
... – select Direction Vector for Path alignment type, – select a direction to which the tool body remains perpendicular, for example, the normal to the planar end face of a cylinder. ...
... – select Direction Vector for Path alignment type, – select a direction to which the tool body remains perpendicular, for example, the normal to the planar end face of a cylinder. ...
Catenary
In physics and geometry, a catenary[p] is the curve that an idealized hanging chain or cable assumes under its own weight when supported only at its ends. The curve has a U-like shape, superficially similar in appearance to a parabola, but it is not a parabola: it is a (scaled, rotated) graph of the hyperbolic cosine. The curve appears in the design of certain types of arches and as a cross section of the catenoid—the shape assumed by a soap film bounded by two parallel circular rings.The catenary is also called the alysoid, chainette, or, particularly in the material sciences, funicular.Mathematically, the catenary curve is the graph of the hyperbolic cosine function. The surface of revolution of the catenary curve, the catenoid, is a minimal surface, specifically a minimal surface of revolution. The mathematical properties of the catenary curve were first studied by Robert Hooke in the 1670s, and its equation was derived by Leibniz, Huygens and Johann Bernoulli in 1691.Catenaries and related curves are used in architecture and engineering, in the design of bridges and arches, so that forces do not result in bending moments. In the offshore oil and gas industry, 'catenary' refers to a steel catenary riser, a pipeline suspended between a production platform and the seabed that adopts an approximate catenary shape.