Download Right Triangle Trig

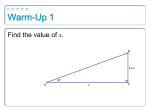
Math 113
Right Triangle Trigonometry Handout
B
(length of hypotenuse) - c
a - (length of side
opposite θ )
θ
A
C
b
(Length of side adjacent to θ )
Pythagorean’s Theorem: for triangles with a right angle ( side 2 + side 2 = hypotenuse 2 )
a 2 + b2 = c2
Two special Right-triangles
1. The “ 45D − 45D − 90D ” right triangle.
We can construct a right triangle with a 45D angle. The triangle has two 45D angles.
Therefore, the triangle is isosceles – that is, it has two sides of the same length. Assume that
1
each leg of the triangle has length
. We can find the length of the hypotenuse using
2
Pythagorean’s Theorem.
1
1
2
45D
1
2
2. The “ 30D − 60D − 90D ” right triangle.
There are two other angles that occur frequently in trigonometry, 30D and 60D . We can find
the values of the trigonometric functions for these angles using a right triangle. To form this
right triangle, draw an equilateral triangle-that is a triangle with all sides the same length.
Assume that each side has a length equal to 1. If we draw a line right down the middle of
this triangle bisecting the top angle and dividing the base into two equal parts, then we will
have a right triangle. See the figure below.
We can find the length of the missing side, a,
using Pythagorean’s Theorem.
30D
1
1
a
60D
60D
1
2
1
2
B
(length of hypotenuse) - c
a - (length of side
opposite θ )
θ
A
C
b
(Length of side adjacent to θ )
The definitions of the six trigonometric functions of the acute angle θ are as follows:
sin θ =
a length of side opposite θ
=
c
length of hypotenuse
csc θ =
c
length of hypotenuse
=
a length of side opposite θ
cos θ =
b length of side adjacent to θ
=
c
length of hypotenuse
sec θ =
c
length of hypotenuse
=
b length of side adjacent to θ
tan θ =
length of side opposite θ
a
=
b length of side adjacent to θ
cot θ =
b length of side adjacent to θ
=
a
length of side opposite θ
Example: Find the value of each of the six trigonometric functions of θ in the figure below.
B
a=3
c
θ
A
C
b=4
sin θ =
a
cos θ =
b
tan θ =
a
c
c
b
=
=
=
Solution: In order to evaluate all six trigonometric functions,
we need to know the length of all sides of the triangle. Since
the lengths for sides a and b are given, we can use
Pythagorean’s Theorem, c 2 = a 2 + b 2 , to find the length of
side c.
opposite
hypotenuse
adjacent
hypotenuse
opposite
adjacent
=
=
csc θ =
=
sec θ =
cot θ =
c
a
c
b
b
a
=
hypotenuse
=
hypotenuse
=
adjacent
opposite
adjacent
opposite
=
=
=
1
1
2
45D
1
2
Now that we know the lengths of the sides of the 45-45-90 right triangle, we can find the six
trigonometric function values for the angle θ = 45D .
sin 45D =
cos 45D =
tan 45D =
opposite
hypotenuse
=
csc 45D =
hypotenuse
=
sec 45D =
hypotenuse
cot 45D =
adjacent
adjacent
hypotenuse
opposite
adjacent
=
opposite
adjacent
opposite
=
=
=
Now that we know the lengths of the sides of the 30-60-90 right triangle, we can find the six
trigonometric function values for both angles θ = 30D and θ = 60D . Using this right triangle
to fill in the blanks below.
opposite
sin 30D =
hypotenuse
30D
3
2
1
60D
cos 30D =
tan 30D =
1
2
sin 60D =
cos 60D =
tan 60D =
adjacent
hypotenuse
opposite
adjacent
opposite
hypotenuse
adjacent
hypotenuse
opposite
adjacent
= __________
= __________
= __________
csc 30D =
sec 30D =
cot 30D =
hypotenuse
opposite
hypotenuse
adjacent
adjacent
opposite
= __________
csc 60D =
hypotenuse
= __________
sec 60D =
hypotenuse
cot 60D =
adjacent
= __________
opposite
adjacent
opposite
= __________
= __________
= __________
= __________
= __________
= __________
The trigonometric function values for an angle θ depend only on the size of the angle θ , and NOT
on the size of the triangle.
a=6
a = 4.5
a=3
θ
θ
b=2
tan θ =
a 3
=
b 2
a = 1.5
b=4
tan θ =
a 3
=
b 2
θ
θ
b =1
tan θ =
a 3
=
b 2
b=3
tan θ =
a 3
=
b 2
Notice that all of these right triangles have the same angle, θ . Even though the triangles are different sizes,
they are “similar”. This means that the triangles have the same shape and the lengths of the corresponding
sides are in the same ratio. Because an acute angle in a right triangle always gives the same ratio of opposite
to adjacent sides, the trigonometric functions’ values evaluated for the angle θ will be the same for all of
these triangles.
Since we know that the size of the triangle is not important, it is helpful to look at right triangles in which the
length of the hypotenuse is equal to 1. Here are our 2 special triangles adjusted so that the length of the
hypotenuse is 1.
The Basic “ 30D − 60D − 90D ” Right Triangle
The Basic “ 45D − 45D − 90D ” Right Triangle
30D
45D
3
2
1
60D
1
1
2
=
2
2
45D
1
2
1
2
=
2
2
Facts:
For any “ 30D − 60D − 90D ” the length of the shortest leg is always
For any “ 30D − 60D − 90D ” the length of the longest leg is always
For any “ 45D − 45D − 90D ” the length of the hypotenuse is always
1
times the length of the hypotenuse.
2
3 times the length of the shortest leg.
2 times the length of a leg.