Download SOLVING SYSTEMS BY GRAPHING INTRODUCTION The objective

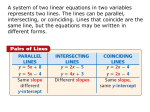
SOLVING SYSTEMS BY GRAPHING
INTRODUCTION
The objective for this lesson on Solving Systems by Graphing is, the student will solve systems of equations by graphing.
The skills students should have in order to help them in this lesson include, solving equations.
We will have three essential questions that will be guiding our lesson. Number one, explain the three possible outcomes
when solving systems of linear equations. Number two, describe the graph of a system of linear equations when there is
only one solution. And number three, how do the graphs differ when comparing a system of equations with no solution
and a system of equations with infinite solutions?
We will begin by completing the warm-up solving equations to prepare for solving systems by graphing in this lesson.
SOLVE PROBLEM – INTRODUCTION
The SOLVE problem for this lesson is, Steve is considering changing gyms. He asked the owners for some data on the
total costs of the gym membership and each provided a table of the values that show the total gym costs after a specific
amount of months. Based on the tables provided, when will the total costs be the same for both gyms?
The table that is provided is seen here.
In Step S, we will Study the Problem. First we need to identify where the question is located within the problem and
underline the question. The question for this problem is, based on the tables provided, when will the total cost be the
same for both gyms?
Now that we have identified the question, we want to put this question in our own words in the form of a statement.
This problem is asking me to find the number of months when the cost will be the same for both gyms.
During this lesson we will learn how to solve systems of linear equations by graphing. We will use this knowledge to
complete this SOLVE problem at the end of the lesson.
SOLVING SYSTEMS BY GRAPHING – ONE SOLUTION
What are the two equations given for Question one? They are y equals negative x plus five and y equals two x minus
four.
Let’s graph these two lines on the coordinate plane.
What form are the lines given in? They are given in slope-intercept form. Which is y equals mx plus b. Where m, which
is the coefficient of x, is the slope and b the number being added to x is the y intercept.
Explain how we graph a linear equation when it’s given in slope-intercept form. We graph the y-intercept and then
apply the slope.
So what is the y-intercept of the first equation? Y equals negative x plus five. The y-intercept is five. Plot the y-intercept
at point (zero, five) on the graph.
What is the slope of the first equation? The coefficient of x in the equation is negative one. So the slope is negative
one, which can also be written as negative one over one.
What should we do after we plot the y-intercept? We need to apply the slope by moving down one unit and to the right
one unit to plot more points. Let’s plot several points now. We go down one unit and to the right one unit to plot each
point. Now we will connect each point together to form a line.
Let’s look at the second equation. What is the y-intercept of the second equation? The y-intercept is negative four.
Plot the y-intercept at the point zero, negative four on the graph. Let’s use a different color to represent this line on the
graph.
What is the slope of the second equation? The slope is two or we can write this as two over one.
What should we do after we plot the y-intercept? Justify your thinking. We need to apply the slope by moving up two
units and to the right one unit to plot more points. Let’s plot several points now. We need to go up two units and to the
right one unit for each point. Once we have several points plotted, we can connect these points to form a line.
Let’s label the lines. Our blue line represents our first equation, which was y equals negative x plus five. And our red
line represents our second equation, which is y equals two x minus four.
When we are solving an equation, what does it mean to find one solution? The solution is the value that when
substituted back into the equation will make the statement true.
Using the equations we began with, let’s substitute some values on the lines into the equations to see if they are
solutions.
For the equations y equals negative x plus five, is the point (zero, five) a solution? Yes. Explain your thinking. If we
substitute zero into the equation for x and substitute five into the equation for y, the left side of the equation simplifies
to five and the right side of the equation also simplifies to five.
Explain your thinking. The equation was y equals negative x plus five. At the point zero, five, x equals zero and y equals
five. When we plug these values into the equation we find that the two sides of the equation are equal.
For the equation y equals two x minus four, is the point (zero, five) a solution? No. Explain your thinking. If we
substitute zero into the equation for x and substitute five into the equation for y, the left side of the equation simplifies
to five and the right side of the equation simplifies to negative four. Therefore a false statement is created and the
point is not a solution.
Y equals two x minus four, when we plug in the points (zero, five) we are plugging in the value of zero for x, and the
value of five for y. When we solve both sides of the equation we find that the two sides are not equal. Five is not equal
to negative four, so therefore the point (zero, five) is not a solution to the second equation.
Is (zero, five) a solution for both equations? No, it is only a solution to the first equation y equals negative x plus five.
Let’s look at another point. Is the point (two, zero) a solution for y equals negative x plus five? Let’s see. If we plug in
the value of zero for y, and two for x, and then find out what the left and the right side of the equation are equal to, we
find that the left side of the equation equals zero and the right side of the equation equals three. Since we find that the
two sides of the equation are not equal, we know that the point two, zero is not a solution for the equation y equals
negative x plus five.
Is the point (two, zero) a solution for y equal two x minus four? Let’s see. We need to plug in the value of y as zero and
the value of x as two. When we simplify both sides of the equation we find that both sides equal zero. Zero is equal to
zero, so yes the point (two, zero) is a solution for the equation y equals two x minus four.
Is the point (two, zero) a solution for both equations? No, it is only a solution to the second equation.
Is the point (three, two) a solution for the equation y equals negative x plus five? Let’s see. We need to take the
equation, and plug in the value of three for x, and the value two for y. When we simplify both sides of the equation, we
find that the two sides are equal to each other. So yes, the point (three, two) is a solution for the equation y equals
negative x plus five.
Is the point (three, two) a solution for the equation y equals two x minus four? Let’s see. We will plug in the value of
three for x and two for y into the equation. When we simplify both sides of the equation we find that the two sides are
equal, so yes the point (three, two) is a solution for the equation y equals two x minus four.
So is the point (three, two) a solution for both equations? Yes, it creates true statements for both equations.
What do you notice about these three points in regard to the lines we plotted? Record your observations.
Let’s talk about these now. What do you notice about the point (zero, five)? This point lies on the first line but not the
second line. What did we find out about the point (zero, five) when we substituted it into the equations? It was a
solution for the first line but not the second.
What do you notice about the point (two, zero)? This point lies on the second line but not the first.
What did we find out about the point (two, zero) when we substituted it into the equations? It was a solution for the
second line but not the first.
And what do you notice about the point (three, two)? This point is found on both lines because it is the intersection
point of both lines.
What did we find out about the point (three, two) when we substituted it into the equations? It was a solution for both
of the equations.
So what conclusions can be drawn from this experiment? Justify your thinking. A solution, in terms of a graph, is a point
that will lie on the graph of a line. The point (zero, five) was a solution to the first equation because the point fell on its
line, just as the point (two, zero) was a solution to the second equation. If a point is going to be a solution to more than
one equation, it must fall on both lines, in which case it will be the one, and only, intersection point.
Therefore, what is the intersection point of the two lines? It is the solution to a system of linear equations.
Plot a point where the two lines intersect on the coordinate plane. This point is plotted at the point (three, two). So
what is the solution to this system of equations? The solution is the point (three, two). X equals three and y equals two.
SOLVING SYSTEMS BY GRAPHING - NO SOLUTION
We are going to continue solving systems by graphing. Take a look at this first equation, x plus y equals six.
Is the first equation in slope-intercept form? No, slope-intercept form is the form y equals mx plus b.
What can we do to put it into slope-intercept for, for easy graphing? Explain your thinking. We can subtract x from each
side of the equation so that y is isolated. Let’s do that now. When we subtract x from each side of the equation, what is
the equation in slope-intercept form? The equation is y equals negative x plus six.
Now let’s look at the second equations, x plus y equals negative one.
Is the second equation in slope-intercept form? No. What can we do to put it into slope-intercept form? Explain your
thinking. We can subtract x from each side of the equation so that y is isolated. Let’s do that now. When we subtract x
from both sides of the equation, what is the equation in slope-intercept form? The equation is y equals negative x
minus one.
Now let’s look at Question two. Is the first equation for Question two in slope-intercept form? The equations is y equals
three x plus two. Yes, this equation is in slope-intercept form.
Is the second equations for Question two in slope-intercept form? The equation is y minus three x equals negative one.
No, this equation is not in slope-intercept form.
So what can we do to change it to slope-intercept form? We can add three x to each side of the equation to that y is
isolated. Let’s do that now. When we add three x to both sides of the equation, what is the equation in slope-intercept
form? The equation is y equals three x minus one.
Now take a moment to graph the lines. Y equals negative x plus six and y equals negative x plus one for Question one.
First let’s graph the equation y equals negative x plus six. The y-intercept is at the point (zero, six). And the slope is
negative one. Let’s plot the line y equals negative x plus six on the graph. Be sure to label the line with the equation.
Now let’s plot the line for y equals negative x minus one on the graph. The slope of the line is negative one and the yintercept is negative one. We have now graphed both lines on the coordinate grid.
What does the graph of the equations look like? It looks like parallel lines.
Now take a moment to graph the lines y equals three x plus two and y equals three x minus one for Question two.
First let’s graph the equation y equals three x plus two. This line has a slope of three and a y-intercept of two. Let’s
graph the line now. Be sure to label the line with the equation.
Now let’s graph the second line, y equals three x minus one. This line has a slope of three and a y-intercept at negative
one. Now what does the graph of the equations look like? It looks like parallel lines.
So what do you notice about the slope of the lines? The slope in each problem is the same value.
What do you notice about the y-intercept of the lines? The y-intercept of each line is different in each problem.
So what conclusion can you make from these equations and graphs? Justify your thinking. If the slopes of the lines are
the same and the y-intercepts are different, the lines are parallel.
Parallel lines never intersect; therefore there will be no solution to this system.
SOLVING SYSTEMS BY GRAPHING – INFINITE SOLUTIONS
Let’s continue solving system by graphing.
Take a look at the first equation seen here. The equation is two x plus two y equals two.
Is the first equation in slope-intercept form? No, slope-intercept form is the form y equals mx plus b.
What can we do to put it into slope-intercept form, for easy graphing? Explain your thinking. We can divide each term
in the equation by two, to begin isolating y. Let’s do that now. When we divide each of the terms in the equation by
two, what is the simplified form of the equation? It is x plus y equals one.
Is the equation in slope-intercept form now? No, remember that slope-intercept form is the form y equals mx plus b.
So what can we do to put it into slope-intercept form? We can subtract x from each side of the equation so that y is
isolated. Let’s do that now. When we subtract x from each side of the equation, what is the equation in slope-intercept
form? It is y equals negative x plus one.
Now let’s look at the second equation, y equals negative x plus one. Is the second equation in slope-intercept form?
Yes.
Let’s now look at the equations for Question two, these equations are four x plus two y equals six and two x plus y
equals three.
Are the equations of Question two in slope-intercept form? No. Take a moment to work through these two equations
and find the slope-intercept form.
For the first equation, four x plus two y equals six, divide each term by two. When we divide each term by two we get
two x plus y equals three.
Next we need to subtract two x from each side. When we subtract two x from each side, the equation in slope-intercept
form is y equals negative two x plus three.
Now let’s look at the second equation in Question two. The equation is two x plus y equals three. For the second
equation we only need to subtract two x from each side. Let’s do that now. When we subtract two x from each side,
the equation written in slope-intercept form is y equals negative two x plus three.
Now that we have changed all equations to slope-intercept form for each graphing, let’s graph the equations for
Problems one and two.
What does the graph of the equations look like for Problem one? Remember that when we changed our first equation
into slope-intercept form we got y equals negative x plus one. This means that the y-intercept will be at the point (zero,
one) and the slope of this line is negative one.
Now for our second equation when written in slope-intercept form, the equation was y equals negative x plus one. This
means that the line will cross the y-axis at the point (zero, one) and it will have a slope of negative one. Let’s graph the
second line now.
What does the graph of the equations look like for problem one? The lines are on top of each other. This means that
they are identical lines.
Now let’s graph the equations for Problem two. When written in slope-intercept form the first equation was y equals
negative two x plus three. This means that the line will cross the y-axis at the point (zero, three) and have a slope of
negative two. Let’s graph the first line now.
For our second equation, when put in slope-intercept form is y equals negative two x plus three. This means that our
second equation will go through the y-axis at the point (zero, three) and have a slope of negative two. Let’s graph the
second line now.
Again, in this example both of the lines are graphed in the same place. So what does the graph of the equations look like
for Problem two? They are identical lines.
So what do you notice about the slope of the lines? The slope in each problem is the same value.
And what do you notice about the y-intercept of the lines? The y-intercept in each problem is also the same value.
So what conclusion can you make from these equations and graphs? If the slope of each line is the same and the yintercepts are the same, the lines are identical. Identical lines intersect at every point on the line, with every
intersection being a solution. Therefore, identical lines have infinite solutions.
SUMMARIZE RESULTS – ANALYZE EQUATIONS
Now that we have seen the three different types of results for resolving systems of linear equations, let’s create a chart
to summarize what we have learned. We will use the graphic organizer seen here to do so.
What three outcomes have we found when solving systems of linear equations? We have found that there can be one
solution, no solutions, or infinite solutions. Let’s record this in the graphic organizer in the first column for the result of
the system. We can have one solution, no solutions, or infinite solutions.
Now is the slope the same or different when the equations only have one solution? The slopes are different. Let’s
record this in the graphic organizer. When a system has one solution the slopes are different.
Are the y-intercepts the same or different when the equations only have one solution? Explain your thinking. The yintercepts can be the same or different. As long as the slopes are different, we can be sure there is only one solution.
So in the box for y-intercept for one solution, let’s write this is not applicable. It is not applicable, because the yintercept has no effect on the outcome if the slopes are different.
How would you describe the lines of the equations that have only one solution? These lines are intersecting. Record the
description of lines for one solution in the graphic organizer.
Now let’s talk about systems that have no solution. Is the slope the same or different when the equations have no
solutions? The slopes are the same. Record this in the graphic organizer.
Are the y-intercepts the same or different when the equations have no solution? The y-intercepts are different. Record
this information in the graphic organizer.
And how would you describe the lines of the equations that have no solutions? The lines are parallel. Record this in the
graphic organizer.
Last let’s talk about systems that have infinite solutions. Is the slope the same or different when the equations have
infinite solutions? The slopes are the same. Record this in the graphic organizer.
Is the y-intercept the same or different when the equations have infinite solutions? The y-intercepts are the same.
Record this in the graphic organizer.
And finally, how would you describe the lines of the equations that have infinite solutions? Explain your thinking. The
lines of equations with infinite solutions are identical. Every point on the line is a solution to the system of equations
when there are infinite solutions and the lines are identical. Record that the lines are identical when the system have
infinite solutions into your graphic organizer.
Now let’s look at a system of equations. The two equations are four x plus y equals nine and y equals negative x minus
seven. Identify if the systems of equations have one solution, no solutions, or infinite solutions.
Let’s look at the first equation. Is the first equation in slope-intercept form? No. So how can we manipulate the
equation so that we can change it to slope-intercept form to quickly identify the slope and y-intercept? Justify your
thinking. We can subtract four x from each side of the equation. What is the equation written in slope-intercept form,
after we subtract four x from each side of the equation? The equations is y equals negative four x plus nine.
So what is the slope of the first equation, now that we have written it in slope-intercept form? The slope is negative
four.
And what is the y-intercept of the first equation? The y-intercept is nine.
Now let’s look at the second equation. Is the second equation in slope-intercept form? Yes. What is the slope of the
second equation? The slope is negative one.
And what is the y-intercept of the second equation? The y-intercept of the second equation is negative seven.
Now looking back at our graphic organizer, what do you think the outcome of the systems of equations will be? This
system of equations will have one solution. Explain your thinking. If we start with the slope, the only scenario where
the slopes are different is the result where there is one solution. This system of equations has one solution.
SOLVE PROBLEM – COMPLETION
We are now going to go back to the SOLVE problem from the beginning of the lesson.
The problem is, Steve is considering changing gyms. He asked the owners for some data on the total costs of the gym
membership and each provided a table of the values that show the total gym costs after a specified amount of months.
Based on the tables provided, when will the total cost be the same for both gyms?
At the beginning of the lesson we, Studied the Problem. First we identified where the question is located within the
problem and underlined the question. We then put this question in our own words in the form of a statement. This
problem is asking me to find the number of months when the costs will be the same for both gyms.
The following table was also provided with the problem.
In Step O, we will Organize the Facts. First we need to identify the facts. Steve is considering changing gyms/fact. He
asked the owners for some data on the total costs of the gym membership/fact, and each provided a table of the values
that show the total gym costs after a specified amount of months/fact. Based on the table provided, when will the total
cost be the same for both gyms?
Now that we have identified the facts we are ready to eliminate the unnecessary facts. These are the facts that will not
help us to find the number of months when the cost will be the same for both gyms. Steve is considering changing
gyms. Knowing that he wants to change gyms, will that help us to find the number of months when the cost will be the
same? No, so we will eliminate this fact. He asked the owners for some data on the total costs of the gym membership.
Knowing that he asked for this data, will that help us to find the number of months when the cost will be the same? No,
so we will eliminate this fact as well. And each provided a table of the values that show the total gym costs after a
specified about of months. The values that they provided that are in the table will help us to find the number of months
when the cost will be the same for both gyms. So we will keep this fact.
Now that we have eliminated the unnecessary facts, we are ready to list the necessary facts. The facts that are
necessary are in the table of values. The table of values creates points for each line:
For Gym A we have a series of points (one, fifty), (three, one hundred ten), and (six, two hundred). What this means is
that at month one the cost is fifty dollars, at month three the total cost for three months is up to one hundred ten
dollars, and at month six the total cost is up to two hundred dollars.
For Gym B, the points are at (one, sixty five), (two, ninety), and (six, one hundred ninety). This means that the first
month the cost for the gym membership is sixty five dollars, after two months the total cost has been up to ninety
dollars, and after six months the total cost is now up to one hundred ninety dollars.
Now in Step L, let’s Line Up A Plan. First write in words what your plan of action will be. We want to plot the points for
Gym A and draw a line. Then plot the points for Gym B and draw a second line. Identify the point where the two lines
intersect. The x-coordinate of the intersection point represents the number of months, so this will tell us when the cost
would be the same.
What operation or operations will we use in our plan? For this plan there is not a specific operation or operations that
will be used. Instead we will be graphing to help us to find our solution.
In Step V, we Verify Your Plan with Action. First estimate your answer. Take a look at the table and see if you can
estimate when the cost will be the same for both gyms. It looks like this will occur sometime between the second and
six months.
Now let’s carry out your plan. We said we wanted to plot the points for Gym A and draw a line. We need to start with a
coordinate grid. The x-axis represents the number of months and the y-axis represents the total cost. For Gym A our
first point is at the point one, fifty. Our second point is at three, one hundred ten. And our third point is at the point six,
two hundred. Let’s connect these points to form a line.
Next we said we would plot the point for Gym B and draw a second line. These points will be at the point, one, sixty five,
two, ninety, and six, one hundred ninety. Connect these points to draw a second line. Now we need to identify the
point where the two lines intersect. Let’s label this point. The x-coordinate of the intersection point represents the
number of months, so this will tell us when the cost would be the same. The two lines intersect at four months. The
lines intersect at the point four, one hundred forty. The x-coordinate represent the number of months, so at four
months, the cost will be the same.
Now in Step E, we Examine Your Results.
Does your answer make sense? Here compare your answer to the question. Yes, because we found when the cost will
be the same.
Is your answer reasonable? Here compare your answer to the estimate. Yes, because four months falls in between two
and six months.
And is your answer accurate? Here check your work. Yes, the answer is accurate.
We are now ready to write your answer in a complete sentence. It will take four months for the gym memberships to
cost the same amount.
CLOSURE
Now let’s go back and discuss the essential question from this lesson.
Our first question was, explain the three possible outcomes when solving systems of linear equations. The outcomes
can be one solution where the graph intersects at one point, no solutions where the graph displays parallel lines with no
intersection, or infinite solutions where the graph contains two identical lines intersecting at infinite locations.
Our second question was, describe the graph of a system of linear equations when there is only one solution. The
solution of a system of equations with one solution will be one value which is graphed as the point of intersection of any
two lines.
And our third question was, how do the graphs differ when comparing a system of equations with no solution and a
system of equations with infinite solutions? The lines of a system with no solution have the same slope and different yintercepts (the lines are parallel), while the lines of a system with infinite solutions have the same slope and the same yintercepts. They are identical lines.