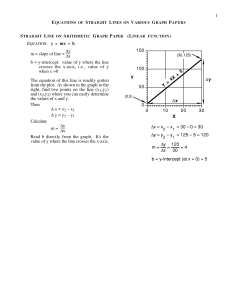
Exponential and Logarithmic Functions Diploma Review
... 13.In the equation y = bx, b > 1, x is replaced by x - 3 and y is replaced by y - 4. Which of the following statements describes the transformation? A. The point (x, y) on the graph of y = bx has been transformed to the point (x + 3, y + 4). B. The point (x, y) on the graph of y = bx has been trans ...
... 13.In the equation y = bx, b > 1, x is replaced by x - 3 and y is replaced by y - 4. Which of the following statements describes the transformation? A. The point (x, y) on the graph of y = bx has been transformed to the point (x + 3, y + 4). B. The point (x, y) on the graph of y = bx has been trans ...
Problem Solving - Gull Lake Community Schools
... of logarithms and exponential functions to simplify equations. Here are two additional properties that are useful for solving equations. • If x y, then bx by. • If x y, then logb x logb y. Use the equation 2x 16 for Exercise 1. 1. a. Express 16 as a power of 2. b. Rewrite the equation so b ...
... of logarithms and exponential functions to simplify equations. Here are two additional properties that are useful for solving equations. • If x y, then bx by. • If x y, then logb x logb y. Use the equation 2x 16 for Exercise 1. 1. a. Express 16 as a power of 2. b. Rewrite the equation so b ...
Pre-Algebra Chapter 8—Linear Functions and Graphing
... 8 Currently, Jodi has a collection of 44 CDs and Veronica has a collection of 22 CDs. Jodi is adding 2 CDs per month to her collection, while Veronica plans to add 4 CDs per month. a. Write a system of equations for this situation. Explain your method. b. Graph the system of equations. c. In how man ...
... 8 Currently, Jodi has a collection of 44 CDs and Veronica has a collection of 22 CDs. Jodi is adding 2 CDs per month to her collection, while Veronica plans to add 4 CDs per month. a. Write a system of equations for this situation. Explain your method. b. Graph the system of equations. c. In how man ...
Itô diffusion

In mathematics — specifically, in stochastic analysis — an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô.