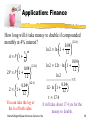Download Chapter 1 Linear Equations and Graphs

Chapter 2
Functions and
Graphs
Section 6
Logarithmic Functions
(Part I)
Learning Objectives for Section 2.6
Logarithmic Functions
 The student will be able to:
• Identify the graphs of one-to-one functions.
• Use and apply inverse functions.
• Evaluate logarithms.
• Rewrite log as exponential functions and vice versa.
Barnett/Ziegler/Byleen Business Calculus 12e
2
One to One Functions
 Definition: A function f is said to be one-to-one if
no x or y values are represented more than once.
• One-to-one:
 𝑓 = { −1, −1 , 0,0 , 1,1 , 2,8 , 3,27 }
• Not one-to-one:
 𝑔 = { −2,4 , −1,1 , 0,0 , 1,1 , 2,4 }
 The graph of a one-to-one function passes both the
vertical and horizontal line tests.
Barnett/Ziegler/Byleen Business Calculus 12e
3
Which Functions Are One to One?
40
12
30
10
8
20
6
10
4
0
-4
-2
0
2
2
4
-10
-20
-30
0
-4
-2
0
2
4
NOT One-to-one
One-to-one
Barnett/Ziegler/Byleen Business Calculus 12e
4
Definition of Inverse Function
 If f is a one-to-one function, then the inverse of f is the
function formed by interchanging the x and y coordinates
for f. Thus, if (a, b) is a point on the graph of f, then (b, a)
is a point on the graph of the inverse of f.
• Let 𝑓 = 2, 5 , 5, 11 , −1, −1 , 0,1
• Then 𝑓 −1 = { 5,2 , 11,5 , −1, −1 , 1,0 }
 The domain of f becomes the range of 𝑓 −1 .
 The range of f becomes the domain of 𝑓 −1 .
 Note: If a function is not one-to-one then f does not have
an inverse.
Barnett/Ziegler/Byleen Business Calculus 12e
5
Finding the Inverse Function
 Given the equation of a one-to-one function f, you can find
𝑓 −1 algebraically by exchanging x for y and solving for y.
 Example: Find 𝑓 −1
𝑥 = −2y − 3
𝑦 = −2x − 3
𝑥 + 3 = −2y
𝑥+3
=y
−2
𝑥+3
−1
𝑓 𝑥 =
−2
Barnett/Ziegler/Byleen Business Calculus 12e
6
Graphs of f and f-1
 The graphs of 𝑓 and 𝑓 −1 are reflections of each other over
the line 𝒚 = 𝒙
 If you know how to graph 𝑓 then simply take a few key
points and switch their x and y coordinates to help you
graph 𝑓 −1 .
 Or find the equation of 𝑓 −1 algebraically first, then graph
it.
Barnett/Ziegler/Byleen Business Calculus 12e
7
Graphs of f and f-1
 Graph 𝑓 and 𝑓 −1 (from the previous example) on the same
coordinate plane.
𝑓 𝑥 = −2x − 3
𝑓 −1
𝑓 −1
𝑥+3
𝑥 =
−2
1
3
𝑥 =− 𝑥−
2
2
𝑓
𝑓 −1
Barnett/Ziegler/Byleen Business Calculus 12e
8
Graphs of f and f-1
 The graph of 𝑓 is shown. Graph 𝑓 −1 .
𝑦=𝑥
Barnett/Ziegler/Byleen Business Calculus 12e
9
Logarithmic Functions
 Exponential functions are one-to-one because they pass the
vertical and horizontal line tests.
𝑦 = 2𝑥
Barnett/Ziegler/Byleen Business Calculus 12e
10
Inverse of an Exponential Function
 Start with the exponential function: 𝑦 = 2𝑥
 Now, interchange x and y: 𝑥 = 2𝑦
 Solving for y: 𝑦 = 𝑙𝑜𝑔2 𝑥
This is called a logarithmic function.
 The inverse of an exponential function is a log function.
𝑓 𝑥 = 2𝑥
𝑓 −1 𝑥 = 𝑙𝑜𝑔2 𝑥
Barnett/Ziegler/Byleen Business Calculus 12e
11
Logarithmic Function
The inverse of an exponential function is called a logarithmic
function. For b > 0 and b  1,
𝐸𝑥𝑝𝑜𝑛𝑒𝑛𝑡𝑖𝑎𝑙
𝑓(𝑥) = 𝑏 𝑥
𝐿𝑜𝑔𝑎𝑟𝑖𝑡ℎ𝑚𝑖𝑐
𝑓 −1 𝑥 = 𝑙𝑜𝑔𝑏 𝑥
𝐷𝑜𝑚𝑎𝑖𝑛: −∞, ∞
𝐷𝑜𝑚𝑎𝑖𝑛: 0, ∞
𝑅𝑎𝑛𝑔𝑒: 0, ∞
𝑅𝑎𝑛𝑔𝑒: −∞, ∞
Barnett/Ziegler/Byleen Business Calculus 12e
12
Graphs
𝐹𝑜𝑟 𝑦 = 2𝑥
D: −∞, ∞ 𝑅: (0, ∞)
D: 0, ∞ 𝑅: −∞, ∞
𝐹𝑜𝑟 𝑦 = log 2 𝑥
Barnett/Ziegler/Byleen Business Calculus 12e
13
Transformations
 Parent function: 𝑦 = 𝑙𝑜𝑔𝑏 𝑥
 Children:
𝑦 = 𝑙𝑜𝑔𝑏 𝑥 + 2
• Shifted up 2
• Shifted right 5
𝑦 = 𝑙𝑜𝑔𝑏 (𝑥 − 5)
• Shifted down 3 and left 7
Barnett/Ziegler/Byleen Business Calculus 12e
𝑦 = 𝑙𝑜𝑔𝑏 𝑥 + 7 − 3
14
Log Notation
 Common Log
• log base 10
• When no base is specified, it’s base 10
• 𝑙𝑜𝑔10 𝑥  log 𝑥
 Natural Log
• log base e
• log 𝑒 𝑥 → ln 𝑥
Barnett/Ziegler/Byleen Business Calculus 12e
15
Simple Logs
 Evaluate each log expression without a calculator:
10
• 𝑙𝑜𝑔2 210
−3
• 𝑙𝑜𝑔5 5−3
2
• 𝑙𝑜𝑔3 9
1
• log 10
•
•
•
•
•
log 0.01
ln 𝑒 7
ln 𝑒
log 1
ln 1
−2
7
1
0
0
Barnett/Ziegler/Byleen Business Calculus 12e
16
Log  Exponential
 Think of the word “log” as meaning “exponent on base b”
 To convert a log equation to an exponential equation:
𝑦 = 𝑙𝑜𝑔3 27
𝑙𝑜𝑔3 27 = 𝑦
• What’s the base? 𝟑
• What’s the exponent? 𝒚
• Write the equation  𝟑𝒚 = 𝟐𝟕
Barnett/Ziegler/Byleen Business Calculus 12e
17
Log  Exponential
Converting a log into an exponential expression:
1. x = log 4 16

4𝑥 = 16
2.
1
log 𝑥
8
= −3

Barnett/Ziegler/Byleen Business Calculus 12e
𝑥 −3
=
1
8
18
Exponential  Log
 To convert an exponential equation to a log equation:
16 = 2𝑦
•
•
•
•
What’s the base? 𝟐
What’s the exponent? 𝒚
Write the equation  𝒚 = 𝒍𝒐𝒈𝟐 𝟏𝟔
Check:
𝒚 = 𝒍𝒐𝒈𝟐 𝟏𝟔
Barnett/Ziegler/Byleen Business Calculus 12e
19
Exponential  Log
Converting an exponential into a log expression:
1.
53 = 125

3 = log 5 125
2.
10𝑥
=
1
100

Barnett/Ziegler/Byleen Business Calculus 12e
𝑥=
1
log10
100
20
Solving Simple Equations
Convert each log to an exponential equation and solve for x:
1. log 𝑥 1000 = 3
𝑥 3 = 1000
3
𝑥 = 1000
𝑥 = 10
2. log 6 𝑥 = 5
65 = 𝑥
𝑥 = 7776
Barnett/Ziegler/Byleen Business Calculus 12e
21
Using Your Calculator
 Use your calculator to evaluate and round to 2 decimal
places:
𝑙𝑛 15 ≈ 2.71
𝑙𝑜𝑔 15 ≈ 1.18
Barnett/Ziegler/Byleen Business Calculus 12e
22
23
Chapter 2
Functions and
Graphs
Section 6
Logarithmic Functions
(Part II)
Learning Objectives for Section 2.6
Logarithmic Functions
 The student will be able to:
• Use log properties.
• Solve log equations.
• Solve exponential equations.
Barnett/Ziegler/Byleen Business Calculus 12e
25
Properties of Logarithms
If b, M, and N are positive real numbers, b  1, and p and x
are real numbers, then
1. log b (1)  0
5. log b MN  log b M  log b N
2. log b (b)  1
M
6. log b
 log b M  log b N
N
7. log b M p  p log b M
3. log b b x  x
4. b
log b x
x
8. log b M  log b N iff M  N
log 𝑥
9. 𝐶ℎ𝑎𝑛𝑔𝑒 𝑜𝑓 𝑏𝑎𝑠𝑒 𝑓𝑜𝑟𝑚𝑢𝑙𝑎: log 𝑏 𝑥 =
log 𝑏
Barnett/Ziegler/Byleen Business Calculus 12e
26
Using Properties
 Rewrite each expression by using the appropriate log
property:
20
= 𝑙𝑜𝑔2 4 = 2
• 𝑙𝑜𝑔2 20 − 𝑙𝑜𝑔2 5 = 𝑙𝑜𝑔2
5
• 𝑙𝑜𝑔5 25𝑥 = 𝑥𝑙𝑜𝑔5 25 = 2𝑥
• log 10𝑥
= log 10 + log 𝑥 = 1 + log 𝑥
• ln 2𝑥 + 1 = ln(5)  2𝑥 + 1 = 5
𝑥=2
• 7𝑙𝑜𝑔7 (𝑥+1) = 𝑥 + 1
log 19
• 𝑙𝑜𝑔3 19 =
≈ 2.68
log 3
Barnett/Ziegler/Byleen Business Calculus 12e
27
Solving Log Equations
Solve for x:




log 4 x  6  log 4 x  6  3
log 4 𝑥 + 6 𝑥 − 6 = 3
log 4 𝑥 2 − 36 = 3
43 = 𝑥 2 − 36
64 = 𝑥 2 − 36
x can’t be -10 because you can’t
take the log of a negative number.
Barnett/Ziegler/Byleen Business Calculus 12e
100 = 𝑥 2
𝑥 = ±10
𝑥 = 10
28
Solving Log Equations
Solve for x. Obtain the exact solution of this equation in
terms of e.
ln (x + 1) – ln x = 1
𝑥+1
𝑙𝑛
=1
𝑥
𝑒1
𝑥+1
=
𝑥
ex - x = 1
x(e - 1) = 1
1
x
e 1
ex = x + 1
Barnett/Ziegler/Byleen Business Calculus 12e
29
Solving Exponential Equations
 Method 1:
• Convert the exponential equation to a log equation.
• Then evaluate.
9𝑥 = 2
𝑥 = 𝑙𝑜𝑔9 2
log 2
𝑥=
log 9
𝑈𝑠𝑖𝑛𝑔 𝐶ℎ𝑎𝑛𝑔𝑒 𝑜𝑓
𝐵𝑎𝑠𝑒 𝐹𝑜𝑟𝑚𝑢𝑙𝑎
𝐱 ≈ 𝟎. 𝟑𝟏𝟓𝟓
Barnett/Ziegler/Byleen Business Calculus 12e
30
Solving Exponential Equations
 Method 2:
• Isolate the exponential part on one side, then take the
log or ln of both sides of the equation.
• Then evaluate.
9𝑥 = 2
log 9𝑥 = log 2
x ∙ log 9 = log 2
log 2
𝑥=
log 9
𝐱 ≈ 𝟎. 𝟑𝟏𝟓𝟓
Barnett/Ziegler/Byleen Business Calculus 12e
31
Solving Exponential Equations
 Solve and round answer to 4 decimal places:
5𝑒 𝑥 = 2
2
𝑥
𝑒 =
5
2
𝑙𝑛 𝑒 = 𝑙𝑛
5
2
1
𝑥 ∙ 𝑙𝑛 𝑒 = 𝑙𝑛
5
2
𝑥 = 𝑙𝑛
5
𝒙 ≈ −𝟎. 𝟗𝟏𝟔𝟑
𝑥
Barnett/Ziegler/Byleen Business Calculus 12e
32
33
Chapter 2
Functions and
Graphs
Section 6
Logarithmic Functions
(Part III)
Learning Objectives for Section 2.6
Logarithmic Functions
 The student will be able to:
• Solve applications involving logarithms.
Barnett/Ziegler/Byleen Business Calculus 12e
35
Application: Finance
How long will it take money to double if compounded
(12∙𝑡)
monthly at 4% interest?
0.04
𝑟
𝐴 =𝑃 1+
𝑛
ln 2 = ln 1 +
𝑛𝑡
0.04
2𝑃 = 𝑃 1 +
12
0.04
2= 1+
12
(12∙𝑡)
(12∙𝑡)
You can take the log or
the ln of both sides.
12
0.04
ln 2 = 12t ∙ ln 1 +
12
ln 2
=t
0.04
12 ∙ ln 1 +
12
𝑡 ≈ 17.4
It will take about 17.4 yrs for the
money to double.
Barnett/Ziegler/Byleen Business Calculus 12e
36
Application: Finance
 Suppose you invest $1500 into an account that is
compounded continuously. At the end of 10 years, you
want to have a balance of $6500. What must the annual
percentage rate be?
13
ln
𝐴 = 𝑃𝑒 𝑟𝑡
6500 = 1500𝑒 (𝑟∙10)
6500
= 𝑒 (𝑟∙10)
1500
13
ln
= ln 𝑒
3
𝑟∙10
Barnett/Ziegler/Byleen Business Calculus 12e
3
= 10𝑟 ∙ ln 𝑒
13
ln 3
=𝑟
10
𝑟 ≈ .147
The annual percentage rate
must be 14.7%
37
Application: Archeology
 Recall from Lesson 2-5 that Carbon-14 decays
according to the model: 𝐴 = 𝐴0 𝑒 −0.000124𝑡
 Estimate that age of a fossil if 15% of the original
amount of C-14 is still present.
0.15 = 1 ∙ 𝑒 (−0.000124∙𝑡)
ln 0.15 = ln 𝑒
ln 0.15
=𝑡
−0.000124
−0.000124∙𝑡
ln 0.15 = −0.000124𝑡 ∙ ln 𝑒
Barnett/Ziegler/Byleen Business Calculus 12e
𝑡 ≈ 15,299
The fossil would be
15,299 years old.
38
Application: Sound Intensity
 Sound intensity is measured using the formula:
𝐼 = 𝐼0 ∙ 10𝑁 10
I = sound intensity in watts per 𝑐𝑚2
𝐼0 = intensity of sound just below the threshold of
hearing = 10−16 𝑊/𝑐𝑚2
N = number of decibels
Barnett/Ziegler/Byleen Business Calculus 12e
39
Application: Sound Intensity
 Solve for N:
𝐼 = 𝐼0 ∙
10𝑁 10
𝐼
= 10𝑁
𝐼0
𝐼
𝑙𝑜𝑔
𝐼0
10
= log(10𝑁
𝐼
𝑙𝑜𝑔 = 𝑁 10
𝐼0
𝐼
𝑁 = 10 ∙ 𝑙𝑜𝑔
𝐼0
10 )
𝐼
𝑙𝑜𝑔 = 𝑁 10 log 10
𝐼0
Barnett/Ziegler/Byleen Business Calculus 12e
40
Application: Sound Intensity
 Use the formula from the previous example to find the
number of decibels for the sound of heavy traffic which
has a sound intensity of 10−8 𝑊/𝑐𝑚2
𝐼
𝑁 = 10 ∙ 𝑙𝑜𝑔
(𝐼0 = 10−16 𝑊/𝑐𝑚2 )
𝐼0
10−8
𝑁 = 10 ∙ 𝑙𝑜𝑔 −16
10
𝑁 = 10 ∙ 𝑙𝑜𝑔108
𝑁 = 10 ∙ 8 ∙ log 10
The sound of heavy traffic is
𝑁 = 80
about 80 decibels.
Barnett/Ziegler/Byleen Business Calculus 12e
41
Logarithmic Regression
When the scatter plot of a data set indicates a slowly
increasing or decreasing function, a logarithmic
function often provides a good model.
We use logarithmic regression on a graphing calculator
to find the function of the form y = a + b*ln(x) that best
fits the data.
Barnett/Ziegler/Byleen Business Calculus 12e
42
Example of Logarithmic
Regression
A cordless screwdriver is sold through a national chain of
discount stores. A marketing company established the following
price-demand table, where x is the number of screwdrivers in
demand each month at a price of p dollars per screwdriver.
x
p = D(x)
1,000
2,000
3,000
4,000
5,000
91
73
64
56
53
Barnett/Ziegler/Byleen Business Calculus 12e
Find a log
regression
equation to predict
the price per
screwdriver if the
demand reaches
6,000.
43
Example of Logarithmic
Regression
x
p = D(x)
1,000
2,000
3,000
4,000
5,000
91
73
64
56
53
𝑦 = 256.47 − 24.04(ln 𝑥)
Barnett/Ziegler/Byleen Business Calculus 12e
44
Example of Logarithmic
Regression
Xmax=6500
Trace
Up arrow
Enter 6000
𝑊ℎ𝑒𝑛 𝑡ℎ𝑒 𝑑𝑒𝑚𝑎𝑛𝑑 𝑖𝑠 6000,
𝑡ℎ𝑒 𝑝𝑟𝑖𝑐𝑒 𝑤𝑖𝑙𝑙 𝑏𝑒 𝑎𝑏𝑜𝑢𝑡 $47.35
Barnett/Ziegler/Byleen Business Calculus 12e
45
46