y - elliottwcms
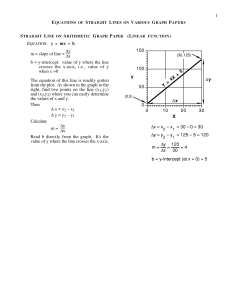
... The y-intercept of a function is the value of y at which the graph of the function crosses the y-axis, or the value of y when x equals 0. When analyzing the y-intercept in a real-world context, this is the starting value of whatever is represented by the y-axis. For example, if the x-axis represents ...
... The y-intercept of a function is the value of y at which the graph of the function crosses the y-axis, or the value of y when x equals 0. When analyzing the y-intercept in a real-world context, this is the starting value of whatever is represented by the y-axis. For example, if the x-axis represents ...
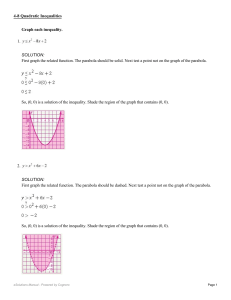
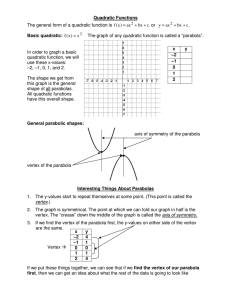
Graph each inequality. 1. SOLUTION: First graph the related function
... First graph the related function. The parabola should be dashed. Next test a point not on the graph of the parabola. ...
... First graph the related function. The parabola should be dashed. Next test a point not on the graph of the parabola. ...
Power Point Version
... b. The solution set includes all points that are on or below the line y = −x. An inequality that describes this region is y ≤ −x, which can also be written x + y ≤ 0. ...
... b. The solution set includes all points that are on or below the line y = −x. An inequality that describes this region is y ≤ −x, which can also be written x + y ≤ 0. ...
a. y
... Start with the other equation. Substitute 2x –1 for y in that equation. Use the Distributive Property. Combine like terms and add 2 to each side. Divide each side by 8. ...
... Start with the other equation. Substitute 2x –1 for y in that equation. Use the Distributive Property. Combine like terms and add 2 to each side. Divide each side by 8. ...
Systems of Linear Equations - Kirkwood Community College
... Many applications involve two (or more) quantities, and by using two (or more) variables, we can form linear equations using the information given. Such a set of equations is called a system, and in this chapter we will develop techniques for solving systems of linear equations. ...
... Many applications involve two (or more) quantities, and by using two (or more) variables, we can form linear equations using the information given. Such a set of equations is called a system, and in this chapter we will develop techniques for solving systems of linear equations. ...
How we solve Diophantine equations
... 2 has an integer solution if and only if it has a real solution and solutions modulo all prime powers. In other words, the obvious necessary conditions are also sufficient. We say that equations of degree 2 satisfy the Hasse principle. This reduces the decision problem to a finite computation, since ...
... 2 has an integer solution if and only if it has a real solution and solutions modulo all prime powers. In other words, the obvious necessary conditions are also sufficient. We say that equations of degree 2 satisfy the Hasse principle. This reduces the decision problem to a finite computation, since ...
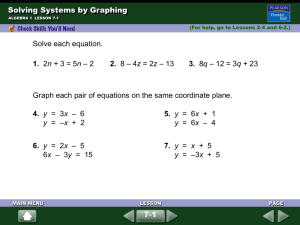
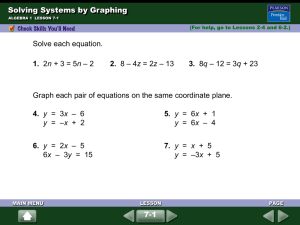
Chapter 7: Solving Systems of Linear Equations and Inequalities
... POPULATION For Exercises 51–54, use the following information. The U.S. Census Bureau divides the country into four sections. They are the Northeast, the Midwest, the South, and the West. 51. In 1990, the population of the Midwest was about 60 million. During the 1990s, the population of this area i ...
... POPULATION For Exercises 51–54, use the following information. The U.S. Census Bureau divides the country into four sections. They are the Northeast, the Midwest, the South, and the West. 51. In 1990, the population of the Midwest was about 60 million. During the 1990s, the population of this area i ...
Graphmatica (page 390)
... GC program — Casio: Distance between 2 points (page 399) GC program — TI: Distance between 2 points (page 399) ...
... GC program — Casio: Distance between 2 points (page 399) GC program — TI: Distance between 2 points (page 399) ...
Homework Solution 5 (p. 331, 2, 4, 6, 7,10,13,17,19, 21, 23) 2. (a
... 23. To solve the system of linear congruences of two variables 13x + 2y ≡ 1 (mod 15), 10x + 9y ≡ 8 (mod 15), the idea is (similar to the linear algebra in solving linear equations) to eliminate one variable, say y. To do so, one naturally wants to multiply 9 on the both sides of the first equation a ...
... 23. To solve the system of linear congruences of two variables 13x + 2y ≡ 1 (mod 15), 10x + 9y ≡ 8 (mod 15), the idea is (similar to the linear algebra in solving linear equations) to eliminate one variable, say y. To do so, one naturally wants to multiply 9 on the both sides of the first equation a ...
A. y - cloudfront.net
... finding the x-intercept and the y-intercept. The x-intercept of a line is the value of x where the line crosses the x-axis (where y = 0). The y-intercept of a line is the value of y where the line crosses the y-axis (where x = 0). ...
... finding the x-intercept and the y-intercept. The x-intercept of a line is the value of x where the line crosses the x-axis (where y = 0). The y-intercept of a line is the value of y where the line crosses the y-axis (where x = 0). ...
in slope-intercept form. - Caldwell County Schools
... through each pair of points in slopeintercept form. 3. (0, 2) and (4, –1) y = – 3 x + 2 ...
... through each pair of points in slopeintercept form. 3. (0, 2) and (4, –1) y = – 3 x + 2 ...