M301.U3.L8 Solving Logarithmic Equations.notebook
... Paleontologists can estimate the size of a dinosaur using only the skull. For a carnivorous dinosaur, the relationship between the length, s , in meters, of the skull and the body mass, m ,in kilograms, can be expressed using the logarithmic equation, ...
... Paleontologists can estimate the size of a dinosaur using only the skull. For a carnivorous dinosaur, the relationship between the length, s , in meters, of the skull and the body mass, m ,in kilograms, can be expressed using the logarithmic equation, ...
1-9
... The school library needs money to complete a new collection. So far, the library has raised $750, which is only one-eighth of what they need. What is the total amount needed? fraction of total ...
... The school library needs money to complete a new collection. So far, the library has raised $750, which is only one-eighth of what they need. What is the total amount needed? fraction of total ...
UNIT 7 Systems of Equations
... Classifying Systems of Linear Equations A system of linear equations is consistent if it has exactly one solution or infinitely many solutions. A consistent system with exactly one solution is a consistent independent system. A consistent system with infinitely many solutions is a consistent depend ...
... Classifying Systems of Linear Equations A system of linear equations is consistent if it has exactly one solution or infinitely many solutions. A consistent system with exactly one solution is a consistent independent system. A consistent system with infinitely many solutions is a consistent depend ...
MATH 1003 Calculus and Linear Algebra (Lecture 5)
... At $0.6 per bottle, the daily supply for milk is 450 bottles, and the daily demand is 570 bottles. When the prices is raised to $0.75 per bottle, the daily supply increases to 600 bottles, and the daily demand decreases to 495 bottles. Assume that the supply and the demand equation are linear. Find ...
... At $0.6 per bottle, the daily supply for milk is 450 bottles, and the daily demand is 570 bottles. When the prices is raised to $0.75 per bottle, the daily supply increases to 600 bottles, and the daily demand decreases to 495 bottles. Assume that the supply and the demand equation are linear. Find ...
Chapter 5
... 6x - 4( -12) = 12 6x + 48 = 12 6x = -36 x = -6 The solution is (–6, –12). 33. 4x + 5y = 0 3x = 6y + 4 Align the x- and y-terms on the left side. 4x + 5y = 0 3x - 6y = 4 To eliminate y, multiply the first equation by 6 and the second equation by 5 and then add. 6[4x + 5y = 0] 5[3x - 6y = 4] gives 24x ...
... 6x - 4( -12) = 12 6x + 48 = 12 6x = -36 x = -6 The solution is (–6, –12). 33. 4x + 5y = 0 3x = 6y + 4 Align the x- and y-terms on the left side. 4x + 5y = 0 3x - 6y = 4 To eliminate y, multiply the first equation by 6 and the second equation by 5 and then add. 6[4x + 5y = 0] 5[3x - 6y = 4] gives 24x ...
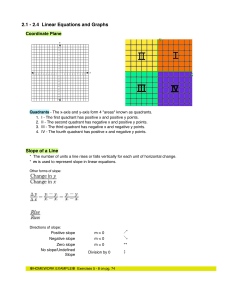
Linear Equation PowerPoint
... 1. Make sure the equation is in slope-intercept form. 2. Identify the slope and y-intercept. 3. Plot the y-intercept. 4. From the y-intercept use the slope to get another point to draw the line. 1. y = 3x + 2 2. Slope = 3 (note that this means the fraction or rise over run could be (3/1) or (-3/-1). ...
... 1. Make sure the equation is in slope-intercept form. 2. Identify the slope and y-intercept. 3. Plot the y-intercept. 4. From the y-intercept use the slope to get another point to draw the line. 1. y = 3x + 2 2. Slope = 3 (note that this means the fraction or rise over run could be (3/1) or (-3/-1). ...
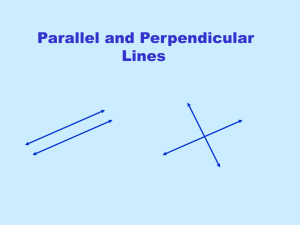
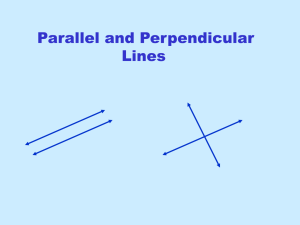
Parallel and Perpendicular Slopes
... first line, y = - 1x ? This is in slope intercept form so y = mx + b which means the slope is –1. ...
... first line, y = - 1x ? This is in slope intercept form so y = mx + b which means the slope is –1. ...