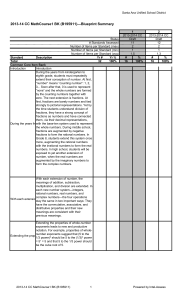
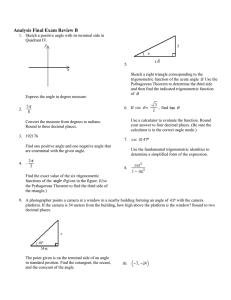
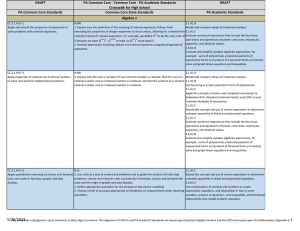
Chapter 3: Algebra: Linear Equations and Functions
... McGraw-Hill’s Math Connects program was conceived and developed with the final results in mind: student success in Algebra 1 and beyond. The authors, using the NCTM Focal Points and Focal Connections as their guide, developed this brand-new series by backmapping from Algebra 1 concepts and verticall ...
... McGraw-Hill’s Math Connects program was conceived and developed with the final results in mind: student success in Algebra 1 and beyond. The authors, using the NCTM Focal Points and Focal Connections as their guide, developed this brand-new series by backmapping from Algebra 1 concepts and verticall ...
Applying Gauss elimination from boolean equation systems to
... parity game. A parity game is a game with two players, played on a graph structure, which represents the original problem in some way. Which of these players wins the game from what starting position, assuming perfect strategy from both players, corresponds to the answer to our original problem. Fur ...
... parity game. A parity game is a game with two players, played on a graph structure, which represents the original problem in some way. Which of these players wins the game from what starting position, assuming perfect strategy from both players, corresponds to the answer to our original problem. Fur ...
BKL singularity
A BKL (Belinsky–Khalatnikov–Lifshitz) singularity is a model of the dynamic evolution of the Universe near the initial singularity, described by an anisotropic, homogeneous, chaotic solution to Einstein's field equations of gravitation. According to this model, the Universe is oscillating (expanding and contracting) around a singular point (singularity) in which time and space become equal to zero. This singularity is physically real in the sense that it is a necessary property of the solution, and will appear also in the exact solution of those equations. The singularity is not artificially created by the assumptions and simplifications made by the other well-known special solutions such as the Friedmann–Lemaître–Robertson–Walker, quasi-isotropic, and Kasner solutions.The Mixmaster universe is a solution to general relativity that exhibits properties similar to those discussed by BKL.