Download PHYS 102 Midterm Exam 2 (09.04.2016) Solutions

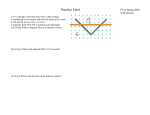
PHYS 102 Midterm Exam 2 (09.04.2016) Solutions
1. Batteries are rated in terms of ampere-hours (A.h). For example, a typical 12 V car battery that can produce
a current of 10.0 A for 6.0 hours is rated at 60 A.h.
(a) (5 Pts.) How much charge does a 60 A.h battery store?
(b) (5 Pts.) What is the total energy (in kilowatt-hours) stored in a 60 A.h battery?
(c) (5 Pts.) If the internal resistance of the battery is 𝑟 = 0.2 Ω, what will be the potential difference between
its terminals when a current of 10 A is drawn from it?
(d) (5 Pts.) In part (c), what percentage of the power will be lost by the internal resistance?
Solution:
(a) Q  I t  (10 A)(6 h)(3600 s / h)  216000 C
(b) P  I V  (10 A)(12V )  120W , U  Pt  (120W )(6 h)(3600 s / h)  2.592 106 J .
Since 1kWh  (1000W )(3600 s)  3.6 106 J , We have U 
2.592 106 J
 0.72 kWh .
3.6 106 J / kWh
(c) V  E  I r  V  (12V )  (10 A)(0.2 )  10V .
(d) Power dissipated by the internal resistance is Pr  I 2 r  (10 A)2 (0.2 )  20W . Therefore, percentage
power loss is
20
 0.17  17%
120
2. Consider the circuit shown in the figure with 𝑉 = 12 𝑉, 𝑅 = 2 Ω and 𝐶 = 1 𝜇𝐹. The capacitor is initially
uncharged, and the switch is closed at time 𝑡 = 0.
R
R
(a) (5 Pts.) Find the currents 𝐼1 , 𝐼2 and 𝐼3 at time 𝑡 = 0.
S
𝐼1
(b) (5 Pts.) Find the currents 𝐼1 , 𝐼2 , 𝐼3 and the charge Q
on the capacitor in the limit 𝑡 → ∞.
(c) (10 Pts.) Find the currents 𝐼1 , 𝐼2 , 𝐼3 and the charge
Q on the capacitor as a function of time t. Verify the
results found in part (a) and (b).
𝐼3
𝐼2
R
C
V
Solution:
(a) At time t  0 the capacitor has no charge
accumulated on it. Therefore, there is no potential drop
across the capacitor, and the equivalent circuit at t  0
is as shown.
R
𝐼1
𝐼3
𝐼2
Writing Kirchhoff’s rules
I1  I 2  I3 , V  I1R  I 2 R  0,  I3 R  I 2 R  0
R
V
and solving the equations for the currents, we find I3  I 2  2 A , and I1  4 A at t  0 .
R
(b) In the limit 𝑡 → ∞, the capacitor is full and no more charge is
accumulated. Therefore, there is no current passing through the
capacitor, and hence, we have I3  0 . The equivalent circuit in the
R
limit 𝑡 → ∞ is as shown.
𝐼1
We have I1  I 2 , V  I1R  I 2 R  0 , which gives
R
𝐼2
V
I1  I 2  3 A , I3  0 .
(c) For any time t, Kirchhoff’s rules give the following equations.
I1  I 2  I3 , V  I1R  I 2 R  0, V  I1R  I3 R VC  0 . Using VC 
dQ
Q
and I 3 
, we get
dt
C
dQ
2
3
V
dQ
dt
, which can be written as
, where   RC . The result can be

Q

dt 3RC
2
3R
(CV / 2)  Q 
1
integrated, and we get Q  CV 1  e t /  .
2


Using 𝑉 = 12 𝑉, 𝑅 = 2 Ω and 𝐶 = 10−6 𝐹, we have   3 106 s , and Q  (6 106 C ) 1  e  t / . So
I3 
6
6
V
dQ
Q
Q
 2 et /(310 ) A. Next V  I1 R  I 3 R   0 gives I1   I 3 
 I1  3  et /(310 ) A .
R
dt
RC
C
Finally I 2  I1  I3 gives I 2  3  et /(310
6
)
A.
Note that when t  0 , we have I1  4 A , I 2  I3  2 A and in the limit t   , I1  I 2  3 A , I3  0 , in
accordance with results of part (a) and (b).
3. (20 Pts.) A Strong magnet is placed under a
horizontal conducting ring of mass m and radius r
which is carrying a current I. If the magnetic field B
makes an angle 𝜃 with the vertical at the ring’s location
at every point, what must be the direction and the
magnitude of the current in order for the ring to be
suspended over the magnet?
ሬ𝑭Ԧ𝑩
𝜃
ሬ𝑩
ሬԦ
𝜃
ሬሬԦ
𝑩
𝜃
𝐼
m
ሬሬԦ
𝒈
Solution:
ሬ𝑭Ԧ𝑩
r
I
N
The direction of the current must be such that net
magnetic force on the current loop must have a
component in the upward direction to balance the
force of gravity. It is equal to the sum of the infinitesimal forces obtained from each infinitesimal current
element taken on the loop. From the figure, we see that at each current segment, the magnetic field is
perpendicular to the current. This results in a force with only radial and vertical components. By symmetry,
we find that the radial force components from segments on opposite sides of the loop cancel. The net force
then is purely vertical and upward. Symmetry also shows us that each current element contributes the same
magnitude of force. Therefore, taking k̂ as the unit vector in the vertical direction, we have
FB   Id  B  IBvkˆ  d  I  B sin   kˆ  2 r  . This force must balance the gravitational force, hence
I 2 r B sin   mg  I 
mg
.
2 rB sin 
4. A point particle with charge q and mass m, moving with velocity v 0  v0 ˆj suddenly enters a region of space
where there is a magnetic field B  B ˆi and an electric field E  E ˆi .
(a) (5 Pts.) What will be the total force on the particle as it enters the region?
(b) (5 Pts.) Writing v  v x ˆi  v y ˆj  vz kˆ for the velocity of the particle at any time later, what will be the
acceleration of the particle at a later time?
(c) (10 Pts.) Writing a 
dv x ˆ dv y ˆ dv z ˆ
i
j
k , find the velocity of the particle as a function of time.
dt
dt
dt
Solution:
(a) F  q (E  v  B)  qE ˆi  q v0 ˆj  ( Bˆi )  qE ˆi  qv0 B kˆ .
(b) At any time later, force on the particle will be
F  q (E  v  B)  qE ˆi  q(v x ˆi  v y ˆj  vzkˆ )  ( Bˆi )  qE ˆi  qvz B ˆj  qvy B kˆ .
So a 
(c)
F q ˆ q
q
 E i  vz B ˆj  v y B kˆ .
m m
m
m
dv dvx ˆ dv y ˆ dvz ˆ
q
q
q

i
j
k  a  E ˆi  vz B ˆj  v y B kˆ . Hence, components of the velocity satisfy
dt
dt
dt
dt
m
m
m
the following equations.
dv y q
dvx q
dv
q
 E,
 vz B , z   v y B .
dt m
dt m
dt
m
The first one is easily integrated to give vx 
q
E t , because vx  0 at time t  0 . To find the other two
m
components we differentiate the equations with respect to t, and use the original equations to write the first
derivative of the velocity components on the right hand side in terms of the components. The result becomes
d 2vy
dt 2
2
d 2v y
qB dvz  qB  qB 
 qB 


vy  
 
 
 vy , and
m dt  m  m 
dt 2
 m
2
d 2 vz
d 2 vz
qB dvy
 qB  qB 
 qB 

 
vz  
 

 vz .
2
2
dt
m dt
dt
 m  m 
 m
Solutions to these equations are of the form A cos (
have vx (0)  0, v y (0)  v0 , we find
vx (t )  v0 sin (
qB
qB
t ), v y (t )  v0 cos ( t ) .
m
m
qB
t   ) , where A and  are constants. Since at t  0 we
m
5. A Let two long parallel wires, a distance 2d apart, carry
equal currents I in the same direction. One wire is at (𝑥 =
−𝑑 , 𝑦 = 0) and the other wire is at (𝑥 = 𝑑 , 𝑦 = 0), both
carrying current I in the z-direction (out of the plane of the
paper).
y
(a) (10 Pts.) Find the magnetic field B on the x-axis for
  x  d , d  x  d , and d  x   .
I
I
(b) (10 Pts.) Find the magnetic field B on the y-axis for
  y   .
x
d
d
Solution:
(a) The direction of the magnetic field at points on the x- axis in the three regions are indicated on the figure.
Therefore, using the expression B 
0 I
for the
2 r
y
magnitude of the magnetic field at a perpendicular
distance r from an infinitely long straight wire carrying a
ሬሬԦ𝟏
𝑩
current I, we have
B
ሬሬԦ𝟏
𝑩
𝐼1
0 I  1
1  ˆ


 ( j), (  x  d ) ,
2  x  d x  d 
B
0 I  1
1


2  d  x d  x
B
0 I  1
1 ˆ


 j , (d  x  ) .
2  x  d x  d 
ሬሬԦ𝟐
𝑩
𝐼2
x
d
d
ሬሬԦ𝟏
𝑩
ሬሬԦ𝟐
𝑩
ሬሬԦ𝟐
𝑩
ˆ
 j , (d  x  d ) ,

(b) For points on the y- axis the direction of the magnetic field is indicated on the figure.
Because of symmetry, the y- components of the magnetic
ሬሬԦ𝟏
𝑩
𝜃
fields cancel each other and we have
I
B  B1  B2  2 0
2
Since sin  
B
y
d 2  y2
 0 I y ˆ
i.
 (d 2  y 2 )
1
d y
2
2
sin  (ˆi )
, we have
y
ሬ𝑩
ሬԦ
𝜃
𝐼1
ሬሬԦ𝟐
𝑩
ඥ𝑑 2 + 𝑦 2
𝑦
𝜃
𝜃
d
d
𝐼2
x