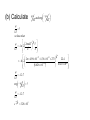Download Chapter 19: Fermi

Chapter 19: Fermi-Dirac
gases
19.1 The Fermi energy
• Fermi-Dirac statistics governs the behavior
of indistinguishable particles (fermions).
• Fermions have a half-integer spin.
• Fermions obey the Pauli exclusion
principle, which prohibits the occupancy of
an available quantum state by more than
one particle.
Fermi function
• Considering an ideal gas comprising N non
interacting fermions, each of mass m
fj 
Nj
gj
1

(  j u )
e
N
f ( ) 

g
kT
1
1
( u )
e
kT
1
• For ε=μ, f(ε) has the value ½ at any temperature.
• μ is the chemical potential and its value at T = 0 ,
μ(0) ,is called the Fermi energy.
• Consider the Fermi function at a temperature of
absolute zero;
 if    ( 0 )
 if    ( 0 )
(   (0)) / kT  {
1 if    ( 0 )
0 if    ( 0 )
f ( )  {
• This tells us that at T = 0 all states with energy
ε<μ(0) are occupied.
• All N particles will be crowded into the N lowest
energy levels.
At T = 0
• There is only one possible configuration
(microstate), i.e. the thermodynamic
probability w is 1.
• According to the Boltzmann relationship, S
= klnW = 0.
how does the Fermi energy μ(0)
depend on m, N, and V?
• Obviously it doesn’t depend on the temperature since T = 0. We need g(ε) ,
the density of quantum states. For particles of spin 1/2 , the spin factor is 2,
18.38
19.2 The calculation of μ(T)
• To obtain these curves, we must
determine μ(T) . The calculation is
considerably more complicated than it was
for T = 0. We have
• the number of particles at T = 0 is the
same as at T ≠ 0,
• At high temperatures the fermion gas
approximates the classical ideal gas. In the
classical limit,
• The spin degeneracy factor is 2 for fermions.
• For T >> TF ,μ/kT takes on a large negative value and exp(-μ/kT)
>>1.
• As an example, consider a kilomole of 3He gas atoms (which are
fermions) at STP. The Fermi temperature is 0.069 K, so that T /TF =
3900. Using eqns (9.16) and (9.17), we find thatμ/kT = -12.7 and
exp(-μ/kT) = 3.3x105. The average occupancy of single particle
states is indeed very small, as in the case of an ideal dilute gas
obeying the M-B distribution.
19.3 Free electrons in a metal
• Electrons are spin 1/2 fermions.
• Statistical thermodynamics provides profound
insights into the behavior of conduction
electrons in metals at moderate temperatures.
• Each atom in the crystal lattice of the metal is
assumed to part with some number of its outer
valence electrons, which can then move freely
about in the metal.
• There is an electric field due to the positive ions
that varies widely from point to point. However,
the effect of the field is canceled out except at
the surface of the metal where there is a strong
potential barrier, called the work function that
draws back into the metal any electron that
happens to make a small excursion outside.
• The free electrons are therefore confined to the
interior of the metal as gas molecules are
confined to the interior of a container.
• In this model, the free electrons move in a potential box
or well whose walls coincide with the boundaries of the
specimen. They occupy energy states up to the so-called
Fermi level, which is the chemical potential μ(T) . The
work function φ is the energy required to remove an
electron at the Fermi level from the metal surface. The
depth of the potential well is equal toμ(T) + φ
The Fermi level of the free electrons in most metals at room temperature is
only fractionally less than the Fermi energy εF. It is often assumed that the
two are equal, and this leads to confusion. The Fermi level, strictly speaking,
is μ(T), which is an approximation to the Fermi energy valid for
T << TF.
A more realistic picture of the potential well is given in the following Figure,
which shows how the potential varies in the vicinity of the positive ions in the
crystal lattice. The periodicity leads to a band structure in the density of
quantum states, which is the foundation of semiconductor physics.
19.2) consider a kilomole of 3He
gas atoms under STP conditions
(a) What is the Fermi temperature of the
gas?
h  N 
TF 


2mk  1.504v 
2
2
3
6.626 10 
 6.023  10 



 27
 23 
2  4.98  10  1.38  10  1.504  22.4 
 0.069 K  0.07 K
 34 2
Fermi Temperature  TF  0.07 K
26
2
3
(b) Calculate


and exp    
kT
kT 

?
kT
we knowthat
  2mkT  3 2 V 

  ln 2

2
kT
h
N

 

3
 

 27
 23
 2
2


4
.
98

10

1
.
38

10

273
22
.
4


  ln 2
2
26

34




6.626  10
 6.023  10 
 



kT
 12.7
exp      ?
kT 


kT
 12.7

e
kT
 3.28 105

(c) Find the average occupancy f   of a
single particle state that has energy of
Energy :   3 kT
2
Chemical Potential :   12.7 kT
Average Occupancy : f    ?
We knowthat
1
f       
KT
e
1
1
 3 12.7 kT
e
2
kT
1
1
1.469  106
f    6.8  10 7

Average
Occupancy  f    6.8 10 7
3 2 kT
19.3) For a system of noninteracting
electrons, show that the probability of
finding an electron in a state with energy ∆
above the chemical potential μ is the same
as the probability of finding an electron
absent from the with energy ∆ below μ at
any given temperature T