Download Intermediate Math Circles October 22, 2008 Number Theory III

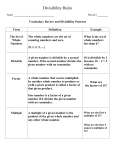
1
University of Waterloo
Faculty of Mathematics
Centre for Education in
Mathematics and Computing
Intermediate Math Circles
October 22, 2008
Number Theory III
Opening Problem
Carolyn and Paul are playing a game starting with a list of the integers 1 to n. The
rules of the game are:
• Carolyn always has the first turn.
• Carolyn and Paul alternate turns.
• On each of her turns, Carolyn must remove one number from the list such that
this number has at least one positive divisor other than itself remaining in the
list.
• On each of his turns, Paul must remove from the list all of the positive divisors
of the number that Carolyn has just removed.
• If Carolyn cannot remove any more numbers, then Paul removes the rest of the
numbers.
For example, if n = 6, a possible sequence of moves is shown in this chart:
Player Number(s) removed Number(s) remaining
Notes
Carolyn
4
1, 2, 3, 5, 6
Paul
1, 2
3, 5, 6
Carolyn
6
3, 5
She could not remove 3 or 5
Paul
3
5
Carolyn
None
5
Carolyn cannot remove any number
Paul
5
None
In this example, the sum of the numbers removed by Carolyn is 4 + 6 = 10 and the
sum of the numbers removed by Paul is 1 + 2 + 3 + 5 = 11.
2
(a) Find a partner. Play the game starting with n = 12 four times, with each of
you going first twice. What was the largest score that the first player ever got?
(b) Suppose that n = 6 and Carolyn removes the integer 2 on her first turn. Determine the sum of the numbers that Carolyn removes and the sum of the numbers
that Paul removes.
(c) Suppose that n = 9 and Carolyn removes the integer 6 on her first turn. What
integer(s) can Carolyn remove on her second turn?
(d) How many prime numbers can Carolyn remove over the course of a game?
(e) If n = 10, determine Carolyn’s maximum possible final sum. Prove that this
sum is her maximum possible sum.
(f) If n = 14, prove that Carolyn cannot remove 7 numbers.
3
Number Theory
Here is a summary of tests for divisibility:
Divisibility by
Test
2
Last digit even
3
Sum of digits divisible by 3
4
# formed by last two digits divisible by 4
5
Last digit 0 or 5
6
Divisible by 2 and 3
7
“Subtract 2 times last digit from rest” algorithm
8
# formed by last three digits divisible by 8
9
Sum of digits divisible by 9
10
Last digit 0
11
Alternating sum digits divisible by 11
12
Divisible by 3 and 4
13
“Add 4 times last digit to rest” algorithm
14
Divisible by 2 and 7
15
Divisible by 3 and 5
Problems:
1. Which of the integers from 2 to 15 are factors of 182754184?
2. Which of the integers from 2 to 15 are factors of 234876153912120?
Why do we we care about being able to do this without a calculator?
4
Problem Set
1. A 4-digit number was written: 86 with the last two digits missing. If the complete number
is exactly divisible by 3, by 4 and by 5, what are the missing digits?
2. If I add up all of the different prime factors of 1998, what answer do I get?
3. What is the sum of all of the prime numbers less than 25?
4. The 8-digit number 1234678 is a multiple of 11. What digit is represented by ?
5. All except four of the nine numbers from 11 to 19 can be put in a single sequence “16, 18, 15,
12, 14” where each successive pair (such as 12 and 14, or 18 and 15) has highest common factor
greater than 1. If you make the longest possible sequence like this using as many as possible of
the nine numbers from 111 to 119, how many numbers will be left out?
6. The two-digit by two-digit multiplication below has lots of gaps, but most them can be filled
in by logic. Do this!
4
×
8
8
0
4
7. Mr. Brown teaches in a high school. The product of the ages of his students is 15 231 236 267 520.
What are the ages of his students?
8. A nine-digit number uses each of the non-zero digits 1 to 9 exactly once. The number itself
has to be divisible by 9. Also, the 8-digit number obtained by removing the last digit is evenly
divisible by 8, the 7-digit number obtained by removing the last two digits is evenly divisible
by 7, and so on. What is the number?
9. If the number A364057B is divisible by 99, find the digits A and B.
10. Given any 16 composite integers less than 2500, at least two will have a prime factor in common.
Explain why this is true.
11. Show that from any five integers, not necessarily distinct, one can always choose three of these
integers whose sum is divisible by 3.
12. You have three piles of stones, containing 5, 49 and 51 stones. You can join any two piles
together into one pile and you can divide a pile with an even number of stones into two piles
of equal size. Can you ever achieve 105 piles, each with one stone? Explain.
13. Determine the value of 102 − 92 + 82 − 72 + 62 − 52 + 42 − 32 + 22 − 12 .
14. A bug in the xy-plane starts at the point (1, 9). It moves first to the point (2, 10) and then to
the point (3, 11), and so on. It continues to move in this way until it reaches a point whose
y-coordinate is twice its x-coordinate. What are the coordinates of this point?
15. If ax3 + bx2 + cx + d = (x2 + x − 2)(x − 4) − (x + 2)(x2 − 5x + 4) for all values of x, what is
the value of a + b + c + d?
5
p
is in lowest terms if p and q have no common factor larger than 1.
q
1 2
70 71
How many of the 71 fractions
, ,..., ,
are in lowest terms?
72 72
72 72
16. A fraction
17. An office building has 50 storeys, 25 of which are painted black and the other 25 of which are
painted gold. If the number of gold storeys in the top half of the building is added to the
number of black storeys in the bottom half of the building, the sum is 28. How many gold
storeys are there in the top half of the building?
18. In the grid shown, each row has a value assigned to it and each column has a value assigned to it. The number in each cell is the
sum of its row and column values. For example, the “8” is the sum of the value assigned to
the 3rd row and the value assigned to the 4th
column. Determine the values of x and y.
3
0
5
6 −2
−2 −5
0
1
y
5
2
x
8
0
0 −3
2
3 −5
−4 −7 −2 −1 −9
19. In the diagram, the semi-circle has centre O and diameter AB. A ray of light leaves point P
in a direction perpendicular to AB. It bounces off the semi-circle at point D in such a way
that ∠P DO = ∠EDO. (In other words, the angle of incidence equals the angle of reflection
at D.) The ray DE then bounces off the circle in a similar way at E before finally hitting the
semicircle again at B. Determine ∠DOP .
E
D
A
P
B
O
20. The number 18 is not the sum of any 2 consecutive positive integers, but is the sum of consecutive positive integers in at least 2 different ways, since 5 + 6 + 7 = 18 and 3 + 4 + 5 + 6 = 18.
Determine a positive integer less than 400 that is not the sum of any 11 consecutive positive
integers, but is the sum of consecutive positive integers in at least 11 different ways.