* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download rotational motion
Tensor operator wikipedia , lookup
Symmetry in quantum mechanics wikipedia , lookup
Brownian motion wikipedia , lookup
Old quantum theory wikipedia , lookup
Laplace–Runge–Lenz vector wikipedia , lookup
Eigenstate thermalization hypothesis wikipedia , lookup
Photon polarization wikipedia , lookup
Internal energy wikipedia , lookup
Mass in special relativity wikipedia , lookup
Mass versus weight wikipedia , lookup
Classical mechanics wikipedia , lookup
Atomic theory wikipedia , lookup
Thermodynamic temperature wikipedia , lookup
Moment of inertia wikipedia , lookup
Theoretical and experimental justification for the Schrödinger equation wikipedia , lookup
Center of mass wikipedia , lookup
Work (physics) wikipedia , lookup
Rotational spectroscopy wikipedia , lookup
Classical central-force problem wikipedia , lookup
Seismometer wikipedia , lookup
Relativistic angular momentum wikipedia , lookup
Equations of motion wikipedia , lookup
Centripetal force wikipedia , lookup
Electromagnetic mass wikipedia , lookup
Kinetic energy wikipedia , lookup
Newton's laws of motion wikipedia , lookup
Hunting oscillation wikipedia , lookup
Rigid body dynamics wikipedia , lookup
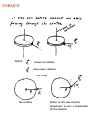
ROTATIONAL MOTION FROM TRANSLATIONAL MOTION Velocity Acceleration 1-D motion 3-D motion Linear momentum TO We have shown that, TO ROTATIONAL MOTION the translational motion of a macroscopic object is equivalent to the translational motion of the CM But this result is not sufficient to describe the motion of a macroscopic object Case A Case B The CM is stationary in both cases Fast spinning slow spinning TORQUE Notice: causes no rotation does cause rotation TOP VIEW No rotation Notice, in this case only the component F2 sinα is responsible for the rotation LATERAL VIEW F A B F TOP VIEW A B Notice also, a force F acting on point B is more effective in rotating the disk than the same force F acting on point A Hence, to attain a more effective rotation, F The vector product Z Y X = = = + + = = = = Z Example = Y = X = = = Practice Practice = = = = = = Let decompose the vector r into two other vectors, one perpendicular to F and another parallel to F r=a + b DESCRIPTION of ROTATIONAL MOTION METHOD: Applying the conservation of mechanical energy CASE: A rotating macroscopic object Rotation Translation Translation A B How do observers A and B apply the concept of conservation of mechanical energy? chapters One specific problem we have in mind is the following: a cylinder rolling down Y ho When applying the conservation of mechanical energy, if the rotational motion were neglected, we would state, ½ m vCM2 + mgy = mg ho 1 But this expression is not correct. We can use the energy of isolated system to treat class of problems concerning the rolling motion of a rigid body down a rough incline. In these cases, the gravitational potential energy of the object-Earth system decreases the rotational and translational kinetic energies of the object increase. For example, consider the sphere rolling without slipping after being released from rest at the top of the inclined. Note that the accelerated rolling motion is possible only if a friction force is present between the the sphere and the incline to produce a net torque about the center of mass. Despite the presence of friction, no loss of mechanical energy occurs because the contact point is at rest relative to the surface at any instant. (On the other hand, if the sphere were to slip, mechanical energy of the sphere-incline-Earth system would be lost due to the kinetic friction force) Ref: Principes of Physics, by Serway and Jewett Kinetic Energy of a System of Particles Z' Z Y' X' Y X ri "i" K= Kinetic energy = = = this is justified in the next page K= Kinetic energy Velocity of measured from the CM with the reference respect to XYZ XYZ Kinetic energy measured from the reference X'Y'Z' (whose origin is attached to the CM of the particles.) ¦ mi vi’ = 0 Justification of i Notice, the position of the center of mass with respect to XYZ is given by rCM = ¦ mi ri i / ¦i mi ri’ O’ ri O rCM rCM’ = ¦ mi ri’ i O’ is the CM of the system of particles / ¦i mi Since the point O’ is the center of mass of the particles, then rCM’ is the vector zero. That is, 0 = ¦ mi r i ’ i 0 = ¦ mi r i ’ / ¦i mi , or i Taking the derivative with respect to time 0 = ¦ mi vi’ i which is what we wanted to justify Example Y' Rolling cylinder X' Y X K = Kinetic energy of the cylinder evaluated from the reference XYZ ½ M v2 + KCM Kinetic energy of the cylinder evaluated from the reference X'Y'Z' Kinetic Energy KCM of a Rotating Z' Rigid Body Z KCM = ω Ri vi' ri' CM X KCM = K= Y Example: I = MR2 EXAMPLE 1: Consider two masses joined by a masless rod. m m d a) What is the momentum of inertia with respect to an axis that passes through the center of mass and that is perpendicular to the rod? m m ICM = m (d/2)2 + m (d/2)2 = m d2 / 2 b) What is the momentum of inertia with respect to an axis passing through one end of the rod? m m I = m (0)2 + m (d)2 = m d2 _____________________________________________________ EXAMPLE 2: Consider two masses joined by a masless rod. m m d a) What is the momentum of inertia with respect to an axis passing through one end? ICM = m (d/2)2 + m (d/2)2 = m d2 / 2 m m d b) What is the momentum of inertia with respect to an axis passing through the center of mass? m ICM = m d2 m d _____________________________________________________ EXAMPLE 3: Consider five masses joined by a masless circular rod. What is the momentum of inertia with respect to an axis passing through the center of mass? m m m ICM = 5 m R2 m R m In the example above, what would be the values of ICM if the ring joining the five masses were not massless, but had a total mass M uniformly distributed? m m M m m R m Answer: ICM = (M + 5m) R2. _____________________________________________________ EXAMPLE 4: Consider of a ring of mass M, and radius R. What is the momentum of inertia with respect to an axis that passes through the CM and that is perpendicular to the plane of the ring? Assume the mass M is uniformly distributed. M ICM = M R2 R _____________________________________________________ EXAMPLE 5: Consider of a ring of mass M, and radius R. What is the momentum of inertia with respect to an axis that passes through the CM and that is in the plane of the ring. Assume the mass M is uniformly distributed. . I = ¦ mi ri2 i The summation turns out to be ri R M = (1/2)M R2 _____________________________________________________ EXAMPLE 6: Consider a thin bar of length d and total mass M (uniformly distributed). M d What is the momentum of inertia with respect to an axis that passes through the center of mass and that is perpendicular to the rod? I = ¦ (dm)i ri2 i ri M The summation turns out to be (dm) i L/ 2 I = ³ L/2 (dm) r2 dm = O dr L/ 2 = ³ L/2 (O dr) r2 = ( O r 3 = ( O>( L ( -L @ L/2 L/2 = ( O>( L@= ( O>( L@ = ( OL>( L@ 0 L Example: Find an expression for the total kinetic energy of a ring of radius R and mass M rolling down an inclined plane K= K= But, what is the relationship between VCM and ω ? Helpful schematic to figure out problems involving rotation without slipping. What is the relationship between: the speed v at which the center-point O advances, and the angular speed ω at which the cylinder of radius R rotates? Translational motion x O ω R O s θ A s A' s=Rθ ds = R ω dt =Rα v B' If there is not slip then, x=s Translational displacement of point "O" 2 Related to the rotational motion Rotational motion 1 x=s v = Rω Relationship between translational and rotational motion Let's go back to our original question: Find an expression for the kinetic energy of a ring of radius R and mass M, rolling an inclined plane.