Download rotational motion

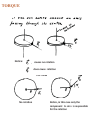
ROTATIONAL MOTION
FROM TRANSLATIONAL MOTION
Velocity
Acceleration
1-D motion
3-D motion
Linear momentum
TO
We have shown that,
TO ROTATIONAL MOTION
the translational motion of a macroscopic object
is equivalent to
the translational motion of the CM
But this result is not sufficient to describe the motion of a
macroscopic object
Case A
Case B
The CM is
stationary in
both cases
Fast
spinning
slow
spinning
TORQUE
Notice:
causes no rotation
does cause rotation
TOP VIEW
No rotation
Notice, in this case only the
component F2 sinα is responsible
for the rotation
LATERAL VIEW
F
A
B F
TOP VIEW
A
B
Notice also,
a force F acting on point B
is more effective in rotating the disk
than the same force F acting on point A
Hence, to attain a more effective rotation,
F
The vector product
Z
Y
X
=
=
= +
+
=
=
=
=
Z
Example
=
Y
=
X
=
=
=
Practice
Practice
=
=
=
=
=
=
Let decompose the vector r into two other vectors,
one perpendicular to F and another parallel to F
r=a + b
DESCRIPTION of ROTATIONAL MOTION
METHOD: Applying the conservation of
mechanical energy
CASE: A rotating macroscopic object
Rotation
Translation
Translation
A
B
How do observers A and B apply the concept of
conservation of mechanical energy?
chapters
One specific problem we have in mind is the following:
a cylinder rolling down
Y
ho
When applying the conservation of
mechanical energy, if the
rotational motion were neglected,
we would state,
½ m vCM2 + mgy = mg ho
1
But this expression is not correct.
We can use the energy of isolated system
to treat class of problems concerning the
rolling motion of a rigid body down a rough incline.
In these cases,
the gravitational potential energy of the object-Earth
system decreases the rotational and translational kinetic energies of
the object increase.
For example, consider the sphere rolling without
slipping after being released from rest at the top of the
inclined.
Note that the accelerated rolling motion is possible only
if a friction force is present between the the sphere and
the incline to produce a net torque about the center of
mass.
Despite the presence of friction, no loss of mechanical
energy occurs because the contact point is at rest
relative to the surface at any instant. (On the other
hand, if the sphere were to slip, mechanical energy of
the sphere-incline-Earth system would be lost due to
the kinetic friction force)
Ref: Principes of Physics, by Serway and Jewett
Kinetic Energy of a System of Particles
Z'
Z
Y'
X'
Y
X
ri
"i"
K=
Kinetic energy
=
=
=
this is justified in
the next page
K=
Kinetic energy
Velocity of
measured from
the CM with
the reference
respect to
XYZ
XYZ
Kinetic energy measured from the
reference X'Y'Z'
(whose origin is attached to the CM of
the particles.)
¦ mi vi’ = 0
Justification of
i
Notice, the position of the center of mass with respect to
XYZ is given by
rCM = ¦ mi ri
i
/ ¦i
mi
ri’
O’
ri
O
rCM
rCM’ = ¦ mi ri’
i
O’ is the CM
of the system
of particles
/ ¦i
mi
Since the point O’ is the center of mass of the particles, then
rCM’ is the vector zero. That is,
0 = ¦ mi r i ’
i
0 = ¦ mi r i ’
/ ¦i
mi
, or
i
Taking the derivative with respect to time
0 = ¦ mi vi’
i
which is what we wanted to justify
Example
Y'
Rolling cylinder
X'
Y
X
K
=
Kinetic energy of
the cylinder
evaluated from the
reference XYZ
½ M v2
+
KCM
Kinetic energy of
the cylinder
evaluated from the
reference X'Y'Z'
Kinetic Energy KCM of a Rotating
Z'
Rigid Body
Z
KCM =
ω
Ri
vi'
ri'
CM
X
KCM =
K=
Y
Example:
I = MR2
EXAMPLE 1: Consider two masses joined by a masless rod.
m
m
d
a) What is the momentum of inertia with respect to an axis that
passes through the center of mass and that is perpendicular to
the rod?
m
m
ICM = m (d/2)2 + m (d/2)2
= m d2 / 2
b) What is the momentum of inertia with respect to an axis passing
through one end of the rod?
m
m
I = m (0)2 + m (d)2
= m d2
_____________________________________________________
EXAMPLE 2: Consider two masses joined by a masless rod.
m
m
d
a) What is the momentum of inertia with respect to an axis passing
through one end?
ICM = m (d/2)2 + m (d/2)2
= m d2 / 2
m
m
d
b) What is the momentum of inertia with respect to an axis passing
through the center of mass?
m
ICM = m d2
m
d
_____________________________________________________
EXAMPLE 3: Consider five masses joined by a masless circular
rod. What is the momentum of inertia with respect to an axis
passing through the center of mass?
m
m
m
ICM = 5 m R2
m
R
m
In the example above, what would be the values of ICM if the ring
joining the five masses were not massless, but had a total mass M
uniformly distributed?
m
m
M
m
m
R
m
Answer: ICM = (M + 5m) R2.
_____________________________________________________
EXAMPLE 4: Consider of a ring of mass M, and radius R. What
is the momentum of inertia with respect to an axis that passes
through the CM and that is perpendicular to the plane of the ring?
Assume the mass M is uniformly distributed.
M
ICM = M R2
R
_____________________________________________________
EXAMPLE 5: Consider of a ring of mass M, and radius R. What
is the momentum of inertia with respect to an axis that passes
through the CM and that is in the plane of the ring. Assume the
mass M is uniformly distributed.
.
I = ¦ mi ri2
i
The summation
turns out to be
ri
R
M
= (1/2)M R2
_____________________________________________________
EXAMPLE 6: Consider a thin bar of length d and total mass M
(uniformly distributed).
M
d
What is the momentum of inertia with respect to an axis that passes
through the center of mass and that is perpendicular to the rod?
I = ¦ (dm)i ri2
i
ri
M
The summation
turns out to be
(dm)
i
L/ 2
I =
³
L/2
(dm) r2
dm = O dr
L/ 2
=
³
L/2
(O dr) r2 = ( O r 3
=
(
O>(
L
(
-L
@
L/2
L/2
= ( O>( L@= ( O>( L@
= ( OL>( L@ 0 L
Example: Find an expression for the total kinetic energy of
a ring of radius R and mass M rolling down an
inclined plane
K=
K=
But, what is the relationship
between VCM and ω ?
Helpful schematic to figure out problems involving rotation
without slipping.
What is the relationship between:
the speed v at which the center-point O advances, and
the angular speed ω at which the cylinder of radius R rotates?
Translational
motion x
O
ω
R
O
s
θ A
s
A'
s=Rθ
ds = R ω
dt
=Rα
v
B'
If there is not slip then,
x=s
Translational
displacement
of point "O"
2
Related to the
rotational motion
Rotational
motion
1
x=s
v = Rω
Relationship between
translational and
rotational motion
Let's go back to our original question:
Find an expression for the
kinetic energy of a ring of
radius R and mass M, rolling
an inclined plane.