* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 23 - UConn Physics
National Electrical Code wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Electricity wikipedia , lookup
Maxwell's equations wikipedia , lookup
Residual-current device wikipedia , lookup
Stray voltage wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Scanning SQUID microscope wikipedia , lookup
History of electric power transmission wikipedia , lookup
Lorentz force wikipedia , lookup
Electrical resistance and conductance wikipedia , lookup
Current source wikipedia , lookup
Earthing system wikipedia , lookup
History of electrochemistry wikipedia , lookup
Mains electricity wikipedia , lookup
Induction heater wikipedia , lookup
Opto-isolator wikipedia , lookup
Electrical injury wikipedia , lookup
High voltage wikipedia , lookup
Alternating current wikipedia , lookup
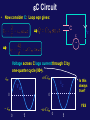
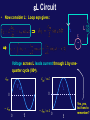
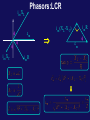
Physics 1402: Lecture 23 Today’s Agenda • Announcements: – RL - RV - RLC circuits • Homework 06: due next Wednesday … • Maxwell’s equations / AC current Induction Self-Inductance, RL Circuits a I I R XXX XXXX XX b L long solenoid Energy and energy density Inductors in Series and Parallel • In series (like resistors) a a L1 Leq L2 And: b b • In parallel (like resistors) a L1 And finally: a L2 b Leq b Summary of E&M • J. C. Maxwell (~1860) summarized all of the work on electric and magnetic fields into four equations, all of which you now know. • However, he realized that the equations of electricity & magnetism as then known (and now known by you) have an inconsistency related to the conservation of charge! Gauss’ Law Faraday’s Law Gauss’ Law For Magnetism Ampere’s Law I don’t expect you to see that these equations are inconsistent with conservation of charge, but you should see a lack of symmetry here! Ampere’s Law is the Culprit! • Gauss’ Law: • Symmetry: both E and B obey the same kind of equation (the difference is that magnetic charge does not exist!) • Ampere’s Law and Faraday’s Law: ! • If Ampere’s Law were correct, the right hand side of Faraday’s Law should be equal to zero -- since no magnetic current. • Therefore(?), maybe there is a problem with Ampere’s Law. • In fact, Maxwell proposes a modification of Ampere’s Law by adding another term (the “displacement” current) to the right hand side of the equation! ie Displacement current Remember: Iin FE Iout changing electric flux Maxwell’s Displacement Current • Can we understand why this “displacement current” has the form it does? • Consider applying Ampere’s Law to the current shown in the diagram. • If the surface is chosen as 1, 2 or 4, the enclosed current = I • If the surface is chosen as 3, the enclosed current = 0! (ie there is no current between the plates of the capacitor) circuit Big Idea: The Electric field between the plates changes in time. “displacement current” ID = 0 (dfE/dt) = the real current I in the wire. Maxwell’s Equations • These equations describe all of Electricity and Magnetism. • They are consistent with modern ideas such as relativity. • They even describe light R C ~ L w i m wL f im wC f m f im R Power Production An Application of Faraday’s Law • You all know that we produce power from many sources. For example, hydroelectric power is somehow connected to the release of water from a dam. How does that work? • Let’s start by applying Faraday’s Law to the following configuration: S S S N N N Side View End View Power Production An Application of Faraday’s Law • Apply Faraday’s Law Power Production An Application of Faraday’s Law • A design schematic Water RLC - Circuits R • Add resistance to circuit: C x 0, r1 r1 .. r1 L 10 n 100 n 1 • Qualitatively: Oscillations created by L and C are damped (energy dissipation!) • Compare to damped oscillations in classical mechanics: f( x ) 0 1 0 5 x 10 AC Circuits - Intro • Last time we discovered that a LC circuit was a natural oscillator. • However, any real attempt to construct a LC circuit must account for the resistance of the inductor. This resistance will cause oscillations to damp out. R + + - x 0, r1 C r1 .. r1 L 10 n 100 n 1 f( x ) 0 1 • Question: Is there any way to modify the circuit above to 0 5 10 x sustain the oscillations without damping? • Answer: Yes, if we can supply energy at the rate the resistor dissipates it! How? A sinusoidally varying emf (AC generator) will sustain sinusoidal current oscillations! AC Circuits Series LCR R • Statement of problem: Given = msinwt , find i(t). Everything else will follow. C ~ L • Procedure: start with loop equation? • We could solve this equation in the same manner we did for the LCR damped circuit. Rather than slog through the algebra, we will take a different approach which uses phasors. R Circuit • Before introducing phasors, per se, begin by considering simple circuits with one element (R,C, or L) in addition to the driving emf. • Begin with R: Loop eqn gives: R ~ Voltage across R in phase with current through R m m / R 0 0 m m / R 0 t x Note: this is always, always, true… always. iR VR 0 iR t Lecture 23, ACT 1a • Consider a simple AC circuit with a purely resistive load. For this circuit the voltage source is = 10V sin (2p50(Hz)t) and R = 5 W. What is the average current in the circuit? A) 10 A B) 5 A C) 2 A D) √2 A R ~ E) 0 A Chapter 28, ACT 1b • Consider a simple AC circuit with a purely resistive load. For this circuit the voltage source is = 10V sin (2p50(Hz)t) and R = 5 W. What is the average power in the circuit? A) 0 W B) 20 W C) 10 W D) 10 √2 W R ~ RMS Values • Average values for I,V are not that helpful (they are zero). • Thus we introduce the idea of the Root of the Mean Squared. • In general, So Average Power is, C Circuit • Now consider C: Loop eqn gives: C ~ iC Voltage across C lags current through C by one-quarter cycle (90). wCm m iC VR 0 0 m wCm 0 t x Is this always true? YES 0 t Lecture 23 , ACT 2 • A circuit consisting of capacitor C and voltage source is constructed as shown. The graph shows the voltage presented to the capacitor as a function of time. – Which of the following graphs best represents the time dependence of the current i in the circuit? i i (a) t i (b) t t C (c) t L Circuit • Now consider L: Loop eqn gives: iL ~ L Voltage across L leads current through L by onequarter cycle (90). m m wL iL VR 0 0 m 0 t x m wL 0 tx Yes, yes, but how to remember? Phasors • R: V in phase with i • C: V lags i by 90 • L: V leads i by 90 • A phasor is a vector whose magnitude is the maximum value of a quantity (eg V or I) and which rotates counterclockwise in a 2-d plane with angular velocity w. Recall uniform circular motion: The projections of r (on the vertical y axis) execute sinusoidal oscillation. y y w x Suppose: xx 00,, r1 r1 .... r1 r1 nn Phasors for L,C,R 11 V i R V f(f(xx))000 xx 00 22 44 66 xx V r1 0 , .. r1 n 1 w i f( x ) 00 0 1.01 1 wt C V 2 4 V i f( x ) 0 0 V C 66 x 1.01 1 R t i x w wt r1 00,, r1 .... r1 r1 n 11 11 i L w i wt L 2 0 2 4 6 Lecture 23, ACT 3 • A series LCR circuit driven by emf = 0sinwt produces a current i=imsin(wt-f). The phasor diagram for the current at t=0 is shown to the right. – At which of the following times is VC, the magnitude of the voltage across the capacitor, a maximum? t=0 f i R i C t=0 t=tc t=tb i (a) i (b) (c) ~ L Series LCR AC Circuit R • Consider the circuit shown here: the loop equation gives: C ~ L • Assume a solution of the form: • Here all unknowns, (im,f) , must be found from the loop eqn; the initial conditions have been taken care of by taking the emf to be: =m sinwt. • To solve this problem graphically, first write down expressions for the voltages across R,C, and L and then plot the appropriate phasor diagram. Phasors: LCR • Given: • Assume: R C L ~ • From these equations, we can draw the phasor diagram to the right. • This picture corresponds to a snapshot at t=0. The projections of these phasors along the vertical axis are the actual values of the voltages at the given time. w i m wL f im wC f m f im R Phasors: LCR w i m XL R C ~ m f L f i m XC f im R • The phasor diagram has been relabeled in terms of the reactances defined from: The unknowns (im,f) can now be solved for graphically since the vector sum of the voltages VL + VC + VR must sum to the driving emf . Phasors:LCR i m XL m f f i m XC f im R i m (XL-X C) m im R f Phasors:Tips y • This phasor diagram was drawn as a snapshot of time t=0 with the voltages being given as the projections along the y-axis. • Sometimes, in working problems, it is easier to draw the diagram at a time when the current is along the x-axis (when i=0). m f i mR imXC m f f i m XC i mX L i m XL f x im R From this diagram, we can also create a triangle which allows us to calculate the impedance Z: Z | XL-XC | | f R “Full Phasor Diagram” “ Impedance Triangle”