Download Oxidation-Reduction Reactions

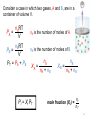
Revision for Exam 2
Ch-4-part of 7
Ch.6
FIRST LAW OF
THERMODYNAMICS
heat energy transferred
∆E = q + w
energy
change
work done
by the
system
Energy is conserved!
ENTHALPY
Most chemical reactions occur at constant P, so
Heat transferred at constant P = qp
qp =
∆H
where H
= enthalpy
and so ∆E = ∆H + w (and w is usually small)
∆H = heat transferred at constant P ≈ ∆E
∆H = change in heat content of the system
∆H = Hfinal - Hinitial
Enthalpy and the First Law of Thermodynamics
DU = q + w
At constant pressure
(happens usually):
q = DH (Enthalpy change) and w = -PDV
DE = DH - PDV
DH = DE + PDV
4
Thermochemical Equations
•
The stoichiometric coefficients always refer to the number
of moles of a substance
H2O (s)
•
DH = 6.01 kJ/mol
If you reverse a reaction, the sign of DH changes
H2O (l)
•
H2O (l)
H2O (s)
DH = -6.01 kJ/mol
If you multiply both sides of the equation by a factor n,
then DH must change by the same factor n.
2H2O (s)
2H2O (l)
DH = 2 x 6.01 = 12.0 kJ
5
The specific heat(s) of a substance is the amount of heat (q)
required to raise the temperature of one gram of the
substance by one degree Celsius.
The heat capacity (C) of a substance is the amount of heat
(q) required to raise the temperature of a given quantity (m)
of the substance by one degree Celsius.
C=mxs
Heat (q) absorbed or released:
q = m x s x Dt
q = C x Dt
Dt = tfinal - tinitial
6
Constant-Volume Calorimetry
qrxn = - (qwater + qbomb)
qwater = m x s x Dt
qbomb = Cbomb x Dt
Reaction at Constant V
DH ~ rxn
No heat enters or leaves!
7
0 ) is the enthalpy of
The standard enthalpy of reaction (DHrxn
a reaction carried out at 1 atm.
aA + bB
cC + dD
DH0rxn = [ cDH0f (C) + dDH0f (D) ] - [ aDH0f (A) + bDH0f (B) ]
DH0rxn = S nDH0f (products) - S mDHf0 (reactants)
DH0 f of any element in its stable form is 0. (Table 6.4)
(
8
Hess’s Law
Hess’s Law: When reactants are converted to
products, the change in enthalpy is the same
whether the reaction takes place in one step
or in a series of steps
Hess’s Law
For example, suppose you are given the
following data:
S(s )  O 2 (g )  SO 2 (g ); DH  -297 kJ
o
2SO 3 (g )  2SO 2 (g )  O 2 (g ); DH  198 kJ
o
Could you use these data to obtain the
enthalpy change for the following
reaction?
2S(s)  3O 2 (g )  2SO 3 (g ); DH  ?
o
Hess’s Law
• If we multiply the first equation by 2 and
reverse the second equation, they will sum
together to become the third.
2S(s )  2O 2 (g )  2SO 2 (g ); DH  (-297 kJ)  (2)
o
2SO 2 (g )  O 2 (g )  2SO 3 (g ); DH o  (198 kJ)  (-1)
2S(s)  3O 2 (g )  2SO 3 (g ); DH  -792 kJ
o
Ch-7
Properties of Waves
Wavelength (l) is the distance between identical points on successive waves.
Amplitude is the vertical distance from the midline of a wave to the peak or
trough.
Frequency (n) is the number of waves that pass through a particular point in 1
second (Hz = 1 cycle/s).
The speed (u) of the wave = l x n
The Wave Nature of Light
• The product of the frequency, n and the wavelength,
l would give the speed of the wave in m/s.
In a vacuum, the speed of light, c, is 3.00 x 108 m/s.
Therefore,
c  nl
So, given the frequency of light, its wavelength can
be calculated, or vice versa.
Quantum Effects and Photons
• Planck’s Quantization of Energy (1900)
According to Max Planck, when solids are heated, they emit
electromagnetic radiation over a wide range of wavelengths.
He proposed that an atom could emit or absorb energy only
in discrete quantities, like small packages, and quantum is
the smallest quantity of that energy for electromagnetic
radiation. The energy E, of a single quantum of energy is
given by,
E  hn
where h (Planck’s constant) is assigned a value of 6.63 x 10-34 J. s
A Problem to Consider
• Calculate the energy of a photon of light emitted
from a hydrogen atom when an electron falls from
level n = 3 to level n = 1.
1 1
E  hn  R h ( 2  2 )
nf ni
E  ( 2.18  10
18
J )( 11  31 )
E  1.94  10
2
18
J
2
Ch.5
Measurement of Gases
• The most important gas laws involve the
relationship between
–
–
–
–
.
number of moles (n) of gas
volume (V)
temperature (T)
pressure (P)
Boyle’s Law
• Boyle’s Law - volume of a gas is
inversely proportional to pressure if the
temperature and number of moles is
held constant.
PV = k1
or
PiVi = PfVf
Charles’ Law
• Charles’ Law - volume of a gas varies
directly with the absolute temperature
(K) if pressure and number of moles of
gas are constant.
V
 k2
T
or
Vi V f

Ti T f
The Empirical Gas Laws
• Gay-Lussac’s Law: The pressure exerted by
a gas at constant volume is directly
proportional to its absolute temperature.
P a Tabs (constant moles and V)
or
Pf
Tf

Pi
Ti
Avogadro’s Law
V a number of moles (n)
Constant temperature
Constant pressure
V = constant x n
V1 / n1 = V2 / n2
21
Ideal Gas Equation
Boyle’s law: P a 1 (at constant n and T)
V
Charles’s law: V a T (at constant n and P)
Avogadro’s law: V a n (at constant P and T)
Va
nT
P
V = constant x
nT
P
=R
nT
P
R is the gas constant
PV = nRT
22
The conditions 0 0C and 1 atm are called standard
temperature and pressure (STP).
Experiments show that at STP, 1 mole of an ideal
gas occupies 22.414 L.
PV = nRT
(1 atm)(22.414L)
PV
R=
=
nT
(1 mol)(273.15 K)
R = 0.082057 L • atm / (mol • K)
23
Density (d) Calculations
PM
m
d=
=
V
RT
m is the mass of the gas in g
M is the molar mass of the gas
PV = nRT, PV = m/M RT, P/RT = m/MV, d= m/V, and
P/RT = d/M , d = PM/RT
Molar Mass (M ) of a Gaseous Substance
dRT
M=
P
d is the density of the gas in g/L
24
Dalton’s Law of Partial Pressures
V and T are constant
P1
P2
Ptotal = P1 + P2
25
Consider a case in which two gases, A and B, are in a
container of volume V.
nART
PA =
V
nBRT
PB =
V
PT = PA + PB
nA is the number of moles of A
nB is the number of moles of B
nA
XA =
nA + nB
Pi = Xi PT
nB
XB =
nA + nB
mole fraction (Xi ) =
ni
nT
26
Gas effusion is the process by which gas under pressure
escapes from one compartment of a container to another by
passing through a small opening. (Fig.5.21)
Gas diffusion is the gradual mixing
of molecules of one gas with
molecules of another by virtue of
their kinetic properties.
r1
r2
=
t2
t1
=

M2
M1
27
Ch.4
An electrolyte is a substance that, when dissolved in
water, results in a solution that can conduct electricity
(dissociates into ions, (strong and weak)).
A nonelectrolyte is a substance that, when dissolved,
results in a solution that does not conduct electricity
(will not dissociate to ions).
nonelectrolyte
weak electrolyte
strong electrolyte
Ionization of acetic acid
CH3COOH
CH3COO- (aq) + H+ (aq)
A reversible reaction. The reaction can
occur in both directions.
Acetic acid is a weak electrolyte because its
ionization in water is incomplete.
Precipitation Reactions
Precipitate – insoluble solid that separates from solution
precipitate
Pb(NO3)2 (aq) + 2NaI (aq)
PbI2 (s) + 2NaNO3 (aq)
molecular equation
Pb2+ (aq) + 2NO3- (aq) + 2Na+ (aq) + 2I- (aq)
PbI2 (s) + 2Na+ (aq) + 2NO3- (aq)
ionic equation
Pb2+ (aq) + 2I- (aq)
PbI2
PbI2 (s)
net ionic equation
Na+ and NO3- are spectator ions
Solubility is the maximum amount of solute that will dissolve
in a given quantity of solvent at a specific temperature.
(insoluble)
(soluble)
Acid-Base Reactions
Acids
Have a sour taste. Vinegar owes its taste to acetic acid. Citrus
fruits contain citric acid.
Cause color changes in plant dyes.
React with certain metals to produce hydrogen gas.
2HCl (aq) + Mg (s)
MgCl2 (aq) + H2 (g)
React with carbonates and bicarbonates to produce carbon
dioxide gas
2HCl (aq) + CaCO3 (s)
CaCl2 (aq) + CO2 (g) + H2O (l)
Aqueous acid solutions conduct electricity.
Types of Chemical Reactions
Acid-Base Reactions
Bronsted-Lowry concept:
Acid: proton donor, Base: proton acceptor
– The Arrhenius concept
acid: proton (H+) donor
base: hydroxide ion (OH-) donor
In summary, both concepts the same
Types of Chemical Reactions
Acid-Base Reactions
• Neutralization Reactions
Canceling the spectator ions results in the
net ionic equation. Note the proton transfer.




H (aq )  Cl (aq )  K (aq )  OH (aq ) 
K  (aq )  Cl  (aq )  H 2O(l )
H  (aq)  OH  (aq)  H 2O(l )
H+
Titrations
In a titration, a solution of accurately known concentration is
added gradually to another solution of unknown concentration
until the chemical reaction between the two solutions is
complete.
Equivalence point – the point at which the reaction is complete
Indicator – substance that changes color at (or near) the
equivalence point
Slowly add base
to unknown acid
UNTIL
the indicator
changes color
Solution Stoichiometry
The concentration of a solution is the amount of solute
present in a given quantity of solvent or solution.
M = molarity =
moles of solute
liters of solution
What mass of KI is required to make 500. mL of
a 2.80 M KI solution?
M KI
volume of KI solution
500. mL x
1L
1000 mL
moles KI
x
2.80 mol KI
1 L soln
x
M KI
166 g KI
1 mol KI
grams KI
= 232 g KI
What volume of a 1.420 M NaOH solution is
Required to titrate 25.00 mL of a 4.50 M H2SO4
solution?
WRITE THE CHEMICAL EQUATION!
H2SO4 + 2NaOH
M
volume acid
25.00 mL x
acid
2H2O + Na2SO4
rx
moles acid
4.50 mol H2SO4
1000 mL soln
x
coef.
M
moles base
2 mol NaOH
1 mol H2SO4
x
base
volume base
1000 ml soln
1.420 mol NaOH
= 158 mL
Types of Chemical Reactions
• Oxidation-Reduction Reactions
Oxidation-reduction reactions involve
the transfer of electrons from one species
to another.
Oxidation is defined as the loss of
electrons.
Reduction is defined as the gain of
electrons.
Oxidation and reduction always occur
simultaneously.
Types of Chemical Reactions
• Oxidation-Reduction Reactions
The reaction of an iron nail with a solution
of copper(II) sulfate, CuSO4, is an
oxidation- reduction reaction
The molecular equation for this reaction is:
Fe(s )  CuSO 4 (aq)  FeSO 4 (aq)  Cu(s )
Types of Chemical Reactions
Oxidation-Reduction Reactions
• Describing Oxidation-Reduction Reactions
An oxidizing agent is a species that oxidizes
another species; it is itself reduced.
A reducing agent is a species that reduces
another species; it is itself oxidized.
Loss of 2 e- oxidation
reducing agent
2
2
Fe(s )  Cu (aq )  Fe (aq )  Cu(s )
oxidizing agent
Gain of 2 e- reduction
Types of Chemical Reactions
Oxidation-Reduction Reactions
• Balancing Simple Oxidation-Reduction Reactions
Adding the two half-reactions together, the
electrons cancel,
2

Zn(s )  Zn (aq )  2e


2Ag (aq )  2e  2Ag(s )
oxidation half-reaction
reduction half-reaction
Zn(s )  2Ag  (aq )  Zn(s)  2Ag(s )
which yields the balanced oxidation-reduction
reaction.
Types of Chemical Reactions
Oxidation-Reduction Reactions
• Oxidation Number Rules
Rule Applies to
Statement
1
The oxidation number of an atom in an
element is zero.
Elements
In compounds or molecules,
2
Monatomic
ions
The oxidation number of an atom in a
monatomic ion equals the charge of the ion.
3
Oxygen
The oxidation number of oxygen is –2 in
most of its compounds. (An exception is O in
H2O2 and other peroxides, where the
oxidation number is –1.)
Types of Chemical Reactions
Oxidation-Reduction Reactions
• Oxidation Number Rules
Rule Applies to
Statement
4
Hydrogen
5
Halogens
6
Compounds
and ions
The oxidation number of hydrogen is +1
except when it is bonded to metals in binary
compounds, where it is -1, eg. LiH
Fluorine is –1 in all its compounds. Each of
the other halogens is –1 in binary compounds
unless the other element is oxygen.
The sum of the oxidation numbers of the
atoms in a compound is zero. The sum in a
polyatomic ion equals the charge on the ion.