* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Oxidation-Reduction Reactions
Atomic theory wikipedia , lookup
History of electrochemistry wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Gas chromatography–mass spectrometry wikipedia , lookup
Photoredox catalysis wikipedia , lookup
Determination of equilibrium constants wikipedia , lookup
Gas chromatography wikipedia , lookup
Nucleophilic acyl substitution wikipedia , lookup
Thermodynamics wikipedia , lookup
Rate equation wikipedia , lookup
History of chemistry wikipedia , lookup
Physical organic chemistry wikipedia , lookup
Water splitting wikipedia , lookup
Marcus theory wikipedia , lookup
Photosynthetic reaction centre wikipedia , lookup
Click chemistry wikipedia , lookup
Acid dissociation constant wikipedia , lookup
Hydrogen-bond catalysis wikipedia , lookup
Bioorthogonal chemistry wikipedia , lookup
Acid–base reaction wikipedia , lookup
Evolution of metal ions in biological systems wikipedia , lookup
Electrolysis of water wikipedia , lookup
Stability constants of complexes wikipedia , lookup
Metalloprotein wikipedia , lookup
Lewis acid catalysis wikipedia , lookup
Chemical equilibrium wikipedia , lookup
Electrochemistry wikipedia , lookup
Chemical reaction wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
Stoichiometry wikipedia , lookup
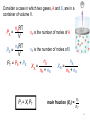
Revision for Exam 2 Ch-4-part of 7 Ch.6 FIRST LAW OF THERMODYNAMICS heat energy transferred ∆E = q + w energy change work done by the system Energy is conserved! ENTHALPY Most chemical reactions occur at constant P, so Heat transferred at constant P = qp qp = ∆H where H = enthalpy and so ∆E = ∆H + w (and w is usually small) ∆H = heat transferred at constant P ≈ ∆E ∆H = change in heat content of the system ∆H = Hfinal - Hinitial Enthalpy and the First Law of Thermodynamics DU = q + w At constant pressure (happens usually): q = DH (Enthalpy change) and w = -PDV DE = DH - PDV DH = DE + PDV 4 Thermochemical Equations • The stoichiometric coefficients always refer to the number of moles of a substance H2O (s) • DH = 6.01 kJ/mol If you reverse a reaction, the sign of DH changes H2O (l) • H2O (l) H2O (s) DH = -6.01 kJ/mol If you multiply both sides of the equation by a factor n, then DH must change by the same factor n. 2H2O (s) 2H2O (l) DH = 2 x 6.01 = 12.0 kJ 5 The specific heat(s) of a substance is the amount of heat (q) required to raise the temperature of one gram of the substance by one degree Celsius. The heat capacity (C) of a substance is the amount of heat (q) required to raise the temperature of a given quantity (m) of the substance by one degree Celsius. C=mxs Heat (q) absorbed or released: q = m x s x Dt q = C x Dt Dt = tfinal - tinitial 6 Constant-Volume Calorimetry qrxn = - (qwater + qbomb) qwater = m x s x Dt qbomb = Cbomb x Dt Reaction at Constant V DH ~ rxn No heat enters or leaves! 7 0 ) is the enthalpy of The standard enthalpy of reaction (DHrxn a reaction carried out at 1 atm. aA + bB cC + dD DH0rxn = [ cDH0f (C) + dDH0f (D) ] - [ aDH0f (A) + bDH0f (B) ] DH0rxn = S nDH0f (products) - S mDHf0 (reactants) DH0 f of any element in its stable form is 0. (Table 6.4) ( 8 Hess’s Law Hess’s Law: When reactants are converted to products, the change in enthalpy is the same whether the reaction takes place in one step or in a series of steps Hess’s Law For example, suppose you are given the following data: S(s ) O 2 (g ) SO 2 (g ); DH -297 kJ o 2SO 3 (g ) 2SO 2 (g ) O 2 (g ); DH 198 kJ o Could you use these data to obtain the enthalpy change for the following reaction? 2S(s) 3O 2 (g ) 2SO 3 (g ); DH ? o Hess’s Law • If we multiply the first equation by 2 and reverse the second equation, they will sum together to become the third. 2S(s ) 2O 2 (g ) 2SO 2 (g ); DH (-297 kJ) (2) o 2SO 2 (g ) O 2 (g ) 2SO 3 (g ); DH o (198 kJ) (-1) 2S(s) 3O 2 (g ) 2SO 3 (g ); DH -792 kJ o Ch-7 Properties of Waves Wavelength (l) is the distance between identical points on successive waves. Amplitude is the vertical distance from the midline of a wave to the peak or trough. Frequency (n) is the number of waves that pass through a particular point in 1 second (Hz = 1 cycle/s). The speed (u) of the wave = l x n The Wave Nature of Light • The product of the frequency, n and the wavelength, l would give the speed of the wave in m/s. In a vacuum, the speed of light, c, is 3.00 x 108 m/s. Therefore, c nl So, given the frequency of light, its wavelength can be calculated, or vice versa. Quantum Effects and Photons • Planck’s Quantization of Energy (1900) According to Max Planck, when solids are heated, they emit electromagnetic radiation over a wide range of wavelengths. He proposed that an atom could emit or absorb energy only in discrete quantities, like small packages, and quantum is the smallest quantity of that energy for electromagnetic radiation. The energy E, of a single quantum of energy is given by, E hn where h (Planck’s constant) is assigned a value of 6.63 x 10-34 J. s A Problem to Consider • Calculate the energy of a photon of light emitted from a hydrogen atom when an electron falls from level n = 3 to level n = 1. 1 1 E hn R h ( 2 2 ) nf ni E ( 2.18 10 18 J )( 11 31 ) E 1.94 10 2 18 J 2 Ch.5 Measurement of Gases • The most important gas laws involve the relationship between – – – – . number of moles (n) of gas volume (V) temperature (T) pressure (P) Boyle’s Law • Boyle’s Law - volume of a gas is inversely proportional to pressure if the temperature and number of moles is held constant. PV = k1 or PiVi = PfVf Charles’ Law • Charles’ Law - volume of a gas varies directly with the absolute temperature (K) if pressure and number of moles of gas are constant. V k2 T or Vi V f Ti T f The Empirical Gas Laws • Gay-Lussac’s Law: The pressure exerted by a gas at constant volume is directly proportional to its absolute temperature. P a Tabs (constant moles and V) or Pf Tf Pi Ti Avogadro’s Law V a number of moles (n) Constant temperature Constant pressure V = constant x n V1 / n1 = V2 / n2 21 Ideal Gas Equation Boyle’s law: P a 1 (at constant n and T) V Charles’s law: V a T (at constant n and P) Avogadro’s law: V a n (at constant P and T) Va nT P V = constant x nT P =R nT P R is the gas constant PV = nRT 22 The conditions 0 0C and 1 atm are called standard temperature and pressure (STP). Experiments show that at STP, 1 mole of an ideal gas occupies 22.414 L. PV = nRT (1 atm)(22.414L) PV R= = nT (1 mol)(273.15 K) R = 0.082057 L • atm / (mol • K) 23 Density (d) Calculations PM m d= = V RT m is the mass of the gas in g M is the molar mass of the gas PV = nRT, PV = m/M RT, P/RT = m/MV, d= m/V, and P/RT = d/M , d = PM/RT Molar Mass (M ) of a Gaseous Substance dRT M= P d is the density of the gas in g/L 24 Dalton’s Law of Partial Pressures V and T are constant P1 P2 Ptotal = P1 + P2 25 Consider a case in which two gases, A and B, are in a container of volume V. nART PA = V nBRT PB = V PT = PA + PB nA is the number of moles of A nB is the number of moles of B nA XA = nA + nB Pi = Xi PT nB XB = nA + nB mole fraction (Xi ) = ni nT 26 Gas effusion is the process by which gas under pressure escapes from one compartment of a container to another by passing through a small opening. (Fig.5.21) Gas diffusion is the gradual mixing of molecules of one gas with molecules of another by virtue of their kinetic properties. r1 r2 = t2 t1 = M2 M1 27 Ch.4 An electrolyte is a substance that, when dissolved in water, results in a solution that can conduct electricity (dissociates into ions, (strong and weak)). A nonelectrolyte is a substance that, when dissolved, results in a solution that does not conduct electricity (will not dissociate to ions). nonelectrolyte weak electrolyte strong electrolyte Ionization of acetic acid CH3COOH CH3COO- (aq) + H+ (aq) A reversible reaction. The reaction can occur in both directions. Acetic acid is a weak electrolyte because its ionization in water is incomplete. Precipitation Reactions Precipitate – insoluble solid that separates from solution precipitate Pb(NO3)2 (aq) + 2NaI (aq) PbI2 (s) + 2NaNO3 (aq) molecular equation Pb2+ (aq) + 2NO3- (aq) + 2Na+ (aq) + 2I- (aq) PbI2 (s) + 2Na+ (aq) + 2NO3- (aq) ionic equation Pb2+ (aq) + 2I- (aq) PbI2 PbI2 (s) net ionic equation Na+ and NO3- are spectator ions Solubility is the maximum amount of solute that will dissolve in a given quantity of solvent at a specific temperature. (insoluble) (soluble) Acid-Base Reactions Acids Have a sour taste. Vinegar owes its taste to acetic acid. Citrus fruits contain citric acid. Cause color changes in plant dyes. React with certain metals to produce hydrogen gas. 2HCl (aq) + Mg (s) MgCl2 (aq) + H2 (g) React with carbonates and bicarbonates to produce carbon dioxide gas 2HCl (aq) + CaCO3 (s) CaCl2 (aq) + CO2 (g) + H2O (l) Aqueous acid solutions conduct electricity. Types of Chemical Reactions Acid-Base Reactions Bronsted-Lowry concept: Acid: proton donor, Base: proton acceptor – The Arrhenius concept acid: proton (H+) donor base: hydroxide ion (OH-) donor In summary, both concepts the same Types of Chemical Reactions Acid-Base Reactions • Neutralization Reactions Canceling the spectator ions results in the net ionic equation. Note the proton transfer. H (aq ) Cl (aq ) K (aq ) OH (aq ) K (aq ) Cl (aq ) H 2O(l ) H (aq) OH (aq) H 2O(l ) H+ Titrations In a titration, a solution of accurately known concentration is added gradually to another solution of unknown concentration until the chemical reaction between the two solutions is complete. Equivalence point – the point at which the reaction is complete Indicator – substance that changes color at (or near) the equivalence point Slowly add base to unknown acid UNTIL the indicator changes color Solution Stoichiometry The concentration of a solution is the amount of solute present in a given quantity of solvent or solution. M = molarity = moles of solute liters of solution What mass of KI is required to make 500. mL of a 2.80 M KI solution? M KI volume of KI solution 500. mL x 1L 1000 mL moles KI x 2.80 mol KI 1 L soln x M KI 166 g KI 1 mol KI grams KI = 232 g KI What volume of a 1.420 M NaOH solution is Required to titrate 25.00 mL of a 4.50 M H2SO4 solution? WRITE THE CHEMICAL EQUATION! H2SO4 + 2NaOH M volume acid 25.00 mL x acid 2H2O + Na2SO4 rx moles acid 4.50 mol H2SO4 1000 mL soln x coef. M moles base 2 mol NaOH 1 mol H2SO4 x base volume base 1000 ml soln 1.420 mol NaOH = 158 mL Types of Chemical Reactions • Oxidation-Reduction Reactions Oxidation-reduction reactions involve the transfer of electrons from one species to another. Oxidation is defined as the loss of electrons. Reduction is defined as the gain of electrons. Oxidation and reduction always occur simultaneously. Types of Chemical Reactions • Oxidation-Reduction Reactions The reaction of an iron nail with a solution of copper(II) sulfate, CuSO4, is an oxidation- reduction reaction The molecular equation for this reaction is: Fe(s ) CuSO 4 (aq) FeSO 4 (aq) Cu(s ) Types of Chemical Reactions Oxidation-Reduction Reactions • Describing Oxidation-Reduction Reactions An oxidizing agent is a species that oxidizes another species; it is itself reduced. A reducing agent is a species that reduces another species; it is itself oxidized. Loss of 2 e- oxidation reducing agent 2 2 Fe(s ) Cu (aq ) Fe (aq ) Cu(s ) oxidizing agent Gain of 2 e- reduction Types of Chemical Reactions Oxidation-Reduction Reactions • Balancing Simple Oxidation-Reduction Reactions Adding the two half-reactions together, the electrons cancel, 2 Zn(s ) Zn (aq ) 2e 2Ag (aq ) 2e 2Ag(s ) oxidation half-reaction reduction half-reaction Zn(s ) 2Ag (aq ) Zn(s) 2Ag(s ) which yields the balanced oxidation-reduction reaction. Types of Chemical Reactions Oxidation-Reduction Reactions • Oxidation Number Rules Rule Applies to Statement 1 The oxidation number of an atom in an element is zero. Elements In compounds or molecules, 2 Monatomic ions The oxidation number of an atom in a monatomic ion equals the charge of the ion. 3 Oxygen The oxidation number of oxygen is –2 in most of its compounds. (An exception is O in H2O2 and other peroxides, where the oxidation number is –1.) Types of Chemical Reactions Oxidation-Reduction Reactions • Oxidation Number Rules Rule Applies to Statement 4 Hydrogen 5 Halogens 6 Compounds and ions The oxidation number of hydrogen is +1 except when it is bonded to metals in binary compounds, where it is -1, eg. LiH Fluorine is –1 in all its compounds. Each of the other halogens is –1 in binary compounds unless the other element is oxygen. The sum of the oxidation numbers of the atoms in a compound is zero. The sum in a polyatomic ion equals the charge on the ion.