Download University Physics: Waves and Electricity Ch22

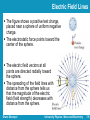
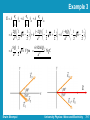
Lecture 7
Ch22. Finding the Electric Field – I
University Physics: Waves and Electricity
Dr.-Ing. Erwin Sitompul
http://zitompul.wordpress.com
2014
The Electric Field
 The Coulomb’s law tells us how a charged particle interacts
with another charged particle.
 The question now: Since the particles do not touch, how can
one particle push or pull the other? How can there be such an
action at a distance with no visible connection between the
particles?
 The concept of Electric Field is introduced to explain this
question.
Erwin Sitompul
University Physics: Wave and Electricity
7/2
The Electric Field
 The electric field is a vector field. It consists of a distribution of
vectors, one for each point in the region around a charged
object.
 We can define the electric field at some point, such at point P,
by placing a positive charge q0, called a test charge.
→
 We then measure the electrostatic force F that acts on the test
charge.
→
 The electric field E at point P is defined as:
F
E
q0
• The direction of
force defines the
direction of field
Erwin Sitompul
University Physics: Wave and Electricity
7/3
The Electric Field
 The positive test charge q0 does not “see” the charged object.
Instead, it “feels” the electric field produced by the charged
object and gives response.
 The SI unit for the electric field is the newton per coulomb
(N/C).
 Note: The field at point P existed both before and after the
test charge was put there.
 Here, we assume that the presence of the
test charge does not affect the charge
distribution on the charged object.
Erwin Sitompul
University Physics: Wave and Electricity
7/4
Electric Field Lines
 In order to understand it better, we will try to visualize the
electric field now.
 Michael Faraday introduced the idea of electric fields in the
19th century and thought of the space around a charged body
as filled with electric field lines .
 The direction of the field lines indicate the direction of the
electric force acting on a positive test charge.
 The density of the field lines is proportional to the magnitude
of the field.
• The field strength is
related to the number of
lines that cross a certain
unit area perpendicular
to the field
Erwin Sitompul
University Physics: Wave and Electricity
7/5
Electric Field Lines
 The figure shows a positive test charge,
placed near a sphere of uniform negative
charge.
 The electrostatic force points toward the
center of the sphere.
 The electric field vectors at all
points are directed radially toward
the sphere.
 The spreading of the field lines with
distance from the sphere tells us
that the magnitude of the electric
field (field strength) decreases with
distance from the sphere.
Erwin Sitompul
University Physics: Wave and Electricity
7/6
Electric Field Lines
 Electric field lines extend away from positive charge (where
they originate) and toward negative charge (where they
terminate).
Erwin Sitompul
University Physics: Wave and Electricity
7/7
Electric Field Lines
 The figure below shows an infinitely large, nonconducting
sheet (or plane) with a uniform distribution of positive charge
on one side.
 Due to symmetry, some forces will cancel one another.
 The net electrostatic force on the positive test charge will be
perpendicular to the sheet and point away from it.
Erwin Sitompul
University Physics: Wave and Electricity
7/8
The Electric Field Due to a Point Charge
 From Coulomb’s law, the electrostatic force due to q1, acting
on a positive test charge q0 is:
F0  k
q0 q1
r10
r̂
2 10
 The electric field due to a point charge q1 is:
F0
q1
E0 
k
r̂
2 10
q0
r10
 The field of a positive point charge is
shown on the right, in vector form.
 The magnitude of the field depends
only on the distance between the point
charge (as the field source) and the
location where the field is measured.
Erwin Sitompul
University Physics: Wave and Electricity
7/9
The Electric Field Due to a Point Charge
 Electric field is a vector quantity.
 Thus, the net, or resultant, electric field due to more than one
point charge is the superposition of the field due to each
charge.
 The net electric field at the position of the test charge, due to
n point charges, is:
E0,net  E01  E02  E03 
q1
k
r10
n
E0,net   k
m 1
Erwin Sitompul
rˆ  k
2 10
qm
rm 0
 E0n
q2
r20
2
rˆ20  k
q3
r30
rˆ 
2 30
k
qn
rn 0
2
rˆn
r̂
2 m0
University Physics: Wave and Electricity
7/10
Checkpoint
The figure below shows a proton p and an electron e on an x
axis.
What is the direction of the electric field due to the electron at:
(a) Point S?
Rightward
Leftward
(b) Point R?
What is the direction of the net electric field at
(c) Point R?
Leftward
(d) Point S?
Rightward
• p and e have the same charge
magnitude
• R and S are closer to e than to p.
Erwin Sitompul
University Physics: Wave and Electricity
7/11
Example 1
A point
→ source q1 = 20 nC is located at S(1,4). Find the electric
field E at P(5,1). All units are in SI.
rS  ˆi  4jˆ
r  5iˆ  ˆj
rSP  rP  rS  (5iˆ  ˆj)  (iˆ  4ˆj)  4iˆ  3jˆ
rSP  (4)2  (3)2  5
rSP 4iˆ  3jˆ
 0.8iˆ  0.6ˆj
rˆSP 

5
rSP
P
• Field at the
measurement
point
• Source charge
E0  k
q1
r10
r̂
2 10
EP  k
qS
rSP
2
r̂SP
9
(20

10
)
ˆ
 8.99 109
(0.8iˆ  0.6j)
2
(5)
 5.754iˆ  4.315jˆ N C
• Vector pointing from
source charge to
measurement point
Erwin Sitompul
University Physics: Wave and Electricity
7/12
Example 2
A point source q1 = 20 nC is located at S(1,4). Determine some
points near S, where the magnitude of the electric field E is
equal to 30 N/C.
EP  k
EP  k
EP  k
qS
rSP
2
E  E • The magnitude of a vector is the
qS
rSP
r̂SP
2
r̂SP
scalar value of the vector itself
r̂  1
qS
rSP 2
(20 109 )
30  8.99 10
rSP 2
9
• The magnitude of a unit vector
always equals 1
(20 109 )
 rSP  8.99 10
30
rSP  2.448 • The points near S must
2
9
be 2.448 m away from S
• Where are they?
Erwin Sitompul
University Physics: Wave and Electricity
7/13
Example 2
y
• Location of points
where the magnitude
of E is equal to 30 N/C
P2
q1
P3
4
+
Some points near S
with E = 30 N/C are:
P1(3.448,4)
P2(1,6.448)
P3(–1.448,4)
P4(1,1.552)
P1
r = 2.448
P4
1
Erwin Sitompul
x
University Physics: Wave and Electricity
7/14
Checkpoint
The figure here shows four situation in which charged particles
are at equal distances from the origin.
Rank the situations according to the magnitude of the net
electric field at the origin, greatest first.
All the same
• Be sure to know
how and why
Erwin Sitompul
University Physics: Wave and Electricity
7/15
Example 3
Three particles with charges q1
= 2Q, q2 = –2Q, and q3 = –4Q,
each with distance d from the
origin, are shown in the figure→
below. What net electric field E
is produced at the origin?
E  E1  E2  E3
q
q
q
 k 1 2 rˆ10  k 2 2 rˆ20  k 3 2 rˆ30
r10
r20
r30
r10  d cos(30)iˆ  d sin(30)jˆ
r20  d cos(150)iˆ  d sin(150)jˆ
r30  d cos(210)iˆ  d sin(210)jˆ
Erwin Sitompul
University Physics: Wave and Electricity
7/16
Example 3
Ek
q1
r10
2
rˆ10  k
q2
r20
2
rˆ20  k
q3
r30
rˆ
2 30
2Q  1 ˆ 1 ˆ 
(2Q)  1 ˆ 1 ˆ 
(4Q)  1 ˆ 1 ˆ 
k 2 
3i  j   k
3i  j   k
3i  j 


2
2
d 2
2 
d  2
2 
d  2
2 
6.928kQ
8Q 1
ˆ
î N C
k 2 
3iV m 
2
d
d 2
E
Erwin Sitompul
University Physics: Wave and Electricity
7/17
A Point Charge in an Electric Field
→
 The electrostatic force F acting
→ on a charged particle
→ located
in an external electric field E has the direction of E if the
charge q of →
the particle is positive and has the opposite
direction of E if negative.
F  qE
 The motion of charged particle can now be analyzed by using
the Newton’s laws. The electrostatic force, if not in check, will
accelerate a charged particle.
Erwin Sitompul
University Physics: Wave and Electricity
7/18
Checkpoint
(a) In the figure, what is the direction
of the electrostatic force on the
electron due to the external field
shown? Leftward
(b) In which direction will the electron
accelerate if it is moving parallel to
the z axis before it encounters the
external field? Leftward
y
E
e
x
(c) If, instead, the electron is initially
moving rightward, will its speed
increase, decrease, or remain
constant?
Decrease
• The direction of force and field are the same on
positive charge, but opposite on negative charge.
• The acceleration has the same direction as the force.
Erwin Sitompul
University Physics: Wave and Electricity
7/19
Measuring the Elementary Charge
 Robert A. Millikan in 1910-1913 devised an apparatus to
measure the elementary charge e.
 When tiny oil drops are sprayed into chamber A, some
become charged, either + or –. They then drift to chamber C.
 If switch S is open, battery B has no
electrical effect on chamber C. If
switch S is closed, the battery
causes the plates to be charged and
set up
→a downward-directed electric
field E in chamber C.
 Negatively charged drop will tend to
drift upward, positively charged drop
will drift downward.
 By timing the motion of oil drops, the
effect of charge q can be
determined, q = ne, where n is
Millikan oil-drop
integer and e = 1.60210–19 C.
apparatus
Erwin Sitompul
University Physics: Wave and Electricity
7/20
Pollination and Electrostatics
 The ability of a bee to transport pollen from flower to flower
depends on the difference of electric charge existing the bee
(positive), the pollen grain (neutral) and the stigma (negative,
because electrically connected to the ground).
Erwin Sitompul
University Physics: Wave and Electricity
7/21
Ink-Jet Printing
 Ink-jet printer is an invention to meet the need for high-quality,
high-speed printing.
 The figure below shows a negatively charged ink drop moving
between two→
conducting plate. A uniform downward-directed
electric field E has been set up.
 The drop is deflected upward and then strikes the→paper at a
position that is determined by the magnitudes of E and the
charge q of the drop.
Erwin Sitompul
University Physics: Wave and Electricity
7/22
Example 4
An ink drop with a mass m of 1.310–10 kg and a negative
charge of magnitude Q = 1.510–13 C enters the region
between the plates of an ink-jet printer. The drop initially moves
along the x axis with the speed vx = 18 m/s. The length L of
each plate is 1.6 cm. The plates are charged and thus produce
an electric field at all points between them.
→
Assume that field E is downward directed, is uniform, and has
a magnitude of 1.4106 N/C.
What is the vertical deflection of the drop at the far edge of the
plates? (The gravitational force on the drop is small relative to
the electrostatic force acting on the drop and can be
neglected.)
Erwin Sitompul
University Physics: Wave and Electricity
7/23
Example 4
F  QE
 (1.5 1013 )(1.4 106 ˆj)
 2.1107 ˆj N
• y direction
F
a
m
2.1 10 7 ˆj

1.3  10 10
 1.615 103 ˆj m s 2
y  y0  v0 yt  12 ayt 2
 (0)(8.889 104 ) 
1
2
(1.615 103 )(8.889 104 ) 2
 6.380 104 m
 0.638 mm
• y direction
• Can you locate where
the 0.638 mm is?
x
1.6 102
t

 8.889 104 s
vx
18
Erwin Sitompul
University Physics: Wave and Electricity
7/24
Homework 6: Three Particles
Three particles are fixed in place and have charges q1 = q2 =
+p and q3 = +2p. Distance a = 6 μm.
What are the magnitude and direction of the net electric field
at point P due to the particles?
p  1.602  1019 C
e  1.602  1019 C
Erwin Sitompul
University Physics: Wave and Electricity
7/25
Homework 6A: Two Particles
1. The figure below shows two charged particles on an x
axis, –q  –3.2×10–19 C at x  –3 m and q  4.8×10–19 C
at x  3 m.
What are the (a) magnitude and (b) direction of the net
electric field produced at point P at y  4 m?
2. (a) A force of 8.4 N directed to the south is applied on a –8.8 μC
charge. Calculate the strength and direction of the electric field at
this point.
(b) What is the magnitude of an electric field at a point in space where
a proton (m = 1.673×10–27 kg) experiences an acceleration of one
million “g”?
Erwin Sitompul
University Physics: Wave and Electricity
7/26
Homework 6B: Four Particles
1. Three charges are placed on three
→ corners of a square. Each side of the
square is 30.0 cm. (a) Compute E at the fourth corner in vector notation.
(b) What would be the force on a 6.00 μC charge placed at the vacant
corner?
Erwin Sitompul
University Physics: Wave and Electricity
7/27