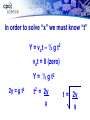Download Chapter 7: Using Vectors: Motion and Force

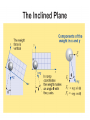
CPO Science
Foundations of Physics
Chapter 9
Unit 3, Chapter 7
Unit 3: Motion and Forces in 2 and 3
Dimensions
Chapter 7 Using Vectors: Forces and Motion
 7.1 Vectors and Direction
 7.2 Projectile Motion and the Velocity
Vector
 7.3 Forces in Two Dimensions
Chapter 7 Objectives
1. Add and subtract displacement vectors to describe
changes in position.
2. Calculate the x and y components of a displacement,
velocity, and force vector.
3. Write a velocity vector in polar and x-y coordinates.
4. Calculate the range of a projectile given the initial
velocity vector.
5. Use force vectors to solve two-dimensional
equilibrium problems with up to three forces.
6. Calculate the acceleration on an inclined plane when
given the angle of incline.
Chapter 7 Vocabulary Terms
 vector
 displacement
 projectile








 trajectory
 Cartesian
coordinates
 range
scalar
magnitude
x-component
y-component
 cosine
 parabola
 Pythagorean
theorem
resultant
position
resolution
right triangle
 sine
 dynamics
 tangent
 velocity vector
 equilibrium
 inclined plane
 normal force
 polar coordinates
 scale component
7.1 Vectors and Direction
Key Question:
How do we accurately
communicate length
and distance?
*Students read Section 7.1 AFTER Investigation 7.1
7.1 Vectors and Direction
 A scalar is a quantity that
can be completely
described by one value:
the magnitude.
 You can think of
magnitude as size or
amount, including units.
7.1 Vectors and Direction
 A vector is a quantity that
includes both magnitude
and direction.
 Vectors require more than
one number.
— The information “1
kilometer, 40 degrees east
of north” is an example of a
vector.
7.1 Vectors and Direction
 In drawing a vector as
an arrow you must
choose a scale.
 If you walk five meters
east, your displacement
can be represented by a
5 cm arrow pointing to
the east.
7.1 Vectors and Direction
 Suppose you walk 5 meters
east, turn, go 8 meters north,
then turn and go 3 meters
west.
 Your position is now 8 meters
north and 2 meters east of
where you started.
 The diagonal vector that
connects the starting position
with the final position is
called the resultant.
7.1 Vectors and Direction
 The resultant is the sum of
two or more vectors added
together.
 You could have walked a
shorter distance by going 2 m
east and 8 m north, and still
ended up in the same place.
 The resultant shows the most
direct line between the
starting position and the final
position.
7.1 Calculate a resultant vector
 An ant walks 2 meters West, 3 meters
North, and 6 meters East.
 What is the displacement of the ant?
7.1 Finding Vector Components
Graphically
 Draw a
displacement vector
as an arrow of
appropriate length
at the specified
angle.
 Mark the angle and
use a ruler to draw
the arrow.
7.1 Finding the Magnitude of a Vector
 When you know the x- and y- components of a vector,
and the vectors form a right triangle, you can find the
magnitude using the Pythagorean theorem.
7.1 Adding Vectors
 Writing vectors in components make it easy to add
them.
7.1 Subtracting Vectors
7.1 Calculate vector magnitude
 A mail-delivery robot
needs to get from where
it is to the mail bin on
the map.
 Find a sequence of two
displacement vectors
that will allow the robot
to avoid hitting the desk
in the middle.
7.2 Projectile Motion and the Velocity
Vector
 Any object that is
moving through the air
affected only by gravity
is called a projectile.
 The path a projectile
follows is called its
trajectory.
7.2 Projectile Motion and the Velocity
Vector
 The trajectory of a
thrown basketball
follows a special type
of arch-shaped curve
called a parabola.
 The distance a
projectile travels
horizontally is called
its range.
7.2 Projectile Motion and the Velocity
Vector
 The velocity vector (v) is a
way to precisely describe
the speed and direction of
motion.
 There are two ways to
represent velocity.
 Both tell how fast and in
what direction the ball
travels.
7.2 Calculate magnitude
Draw the velocity vector
v = (5, 5) m/sec and
calculate the magnitude
of the velocity (the
speed), using the
Pythagorean theorem.
7.2 Components of the Velocity Vector
 Suppose a car is driving
20 meters per second.
 The direction of the
vector is 127 degrees.
 The polar representation
of the velocity is v = (20
m/sec, 127°).
7.2 Calculate velocity
 A soccer ball is kicked at a speed of 10 m/s and an
angle of 30 degrees.
 Find the horizontal and vertical components of the
ball’s initial velocity.
7.2 Adding Velocity Components
 Sometimes the total velocity of an object is a
combination of velocities.
 One example is the motion of a boat on a river.
 The boat moves with a certain velocity relative to the
water.
 The water is also moving with another velocity relative to
the land.
7.2 Adding Velocity Components
7.2 Calculate velocity components
 An airplane is moving at a velocity of 100 m/s in a
direction 30 degrees NE relative to the air.
 The wind is blowing 40 m/s in a direction 45 degrees SE
relative to the ground.
 Find the resultant velocity of the airplane relative to the
ground.
7.2 Projectile Motion
Vx
 When we drop a ball
from a height we know
that its speed
increases as it falls.
 The increase in speed
is due to the
acceleration gravity, g
= 9.8 m/sec2.
Vy
y
x
7.2 Horizontal Speed
 The ball’s horizontal
velocity remains constant
while it falls because
gravity does not exert any
horizontal force.
 Since there is no force, the
horizontal acceleration is
zero (ax = 0).
 The ball will keep moving
to the right at 5 m/sec.
7.2 Horizontal Speed
 The horizontal distance a projectile moves can
be calculated according to the formula:
7.2 Vertical Speed
 The vertical speed (vy) of the
ball will increase by 9.8
m/sec after each second.
 After one second has
passed, vy of the ball will be
9.8 m/sec.
 After the 2nd second has
passed, vy will be 19.6 m/sec
and so on.
7.2 Calculate using projectile motion
 A stunt driver steers a car
off a cliff at a speed of 20
meters per second.
 He lands in the lake below
two seconds later.
 Find the height of the cliff
and the horizontal
distance the car travels.
7.2 Projectiles Launched at an Angle
 A soccer ball kicked
off the ground is
also a projectile, but
it starts with an
initial velocity that
has both vertical
and horizontal
components.
*The launch angle determines how the initial velocity
divides between vertical (y) and horizontal (x) directions.
7.2 Steep Angle
 A ball launched
at a steep angle
will have a large
vertical velocity
component and a
small horizontal
velocity.
7.2 Shallow Angle
 A ball launched at
a low angle will
have a large
horizontal velocity
component and a
small vertical one.
7.2 Projectiles Launched at an Angle
The initial velocity components of an object launched at a
velocity vo and angle θ are found by breaking the
velocity into x and y components.
7.2 Range of a Projectile
 The range, or horizontal distance, traveled by a
projectile depends on the launch speed and the
launch angle.
7.2 Range of a Projectile
 The range of a projectile is calculated from the
horizontal velocity and the time of flight.
7.2 Range of a Projectile
 A projectile travels farthest when launched at
45 degrees.
7.2 Range of a Projectile
 The vertical velocity is responsible for giving
the projectile its "hang" time.
7.2 "Hang Time"
 You can easily calculate your own hang time.
 Run toward a doorway and jump as high as you can,
touching the wall or door frame.
 Have someone watch to see exactly how high you
reach.
 Measure this distance with a meter stick.
 The vertical distance formula can be rearranged to
solve for time:
7.2 Projectile Motion and the Velocity
Vector
Key Question:
Can you predict the landing spot of a projectile?
*Students read Section 7.2 BEFORE Investigation 7.2
Marble’s Path
Vx
t=?
Vy
y
x=?
In order to solve “x” we must know “t”
Y = vot – ½ g t2
vot = 0 (zero)
Y = ½ g t2
2y = g t2
t2 = 2y
g
t = 2y
g
7.3 Forces in Two Dimensions
 Force is also represented in x-y components.
7.3 Force Vectors
 If an object is in
equilibrium, all of the
forces acting on it are
balanced and the net
force is zero.
 If the forces act in two
dimensions, then all of
the forces in the xdirection and y-direction
balance separately.
7.3 Equilibrium and Forces
 It is much more difficult
for a gymnast to hold
his arms out at a 45degree angle.
 To see why, consider
that each arm must still
support 350 newtons
vertically to balance the
force of gravity.
7.3 Forces in Two Dimensions
 Use the y-component to find the total force in the
gymnast’s left arm.
7.3 Forces in Two Dimensions
 The force in the right arm must also be 495 newtons
because it also has a vertical component of 350 N.
7.3 Forces in Two Dimensions
 When the gymnast’s arms
are at an angle, only part
of the force from each
arm is vertical.
 The total force must be
larger because the
vertical component of
force in each arm must
still equal half his weight.
7.3 Forces and Inclined Planes
 An inclined plane is a straight surface, usually
with a slope.
 Consider a block sliding
down a ramp.
 There are three forces
that act on the block:
— gravity (weight).
— friction
— the reaction force
acting on the block.
7.3 Forces and Inclined Planes
 When discussing forces, the word “normal”
means “perpendicular to.”
 The normal force
acting on the block is
the reaction force
from the weight of the
block pressing
against the ramp.
7.3 Forces and Inclined Planes
 The normal force
on the block is
equal and
opposite to the
component of the
block’s weight
perpendicular to
the ramp (Fy).
7.3 Forces and Inclined Planes
 The force parallel
to the surface (Fx)
is given by
Fx = mg sinθ.
7.3 Acceleration on a Ramp
 Newton’s second law can be used to calculate the
acceleration once you know the components of all the
forces on an incline.
 According to the second law:
Acceleration
(m/sec2)
a=F
m
Force (kg . m/sec2)
Mass (kg)
7.3 Acceleration on a Ramp
 Since the block can only accelerate along the ramp, the
force that matters is the net force in the x direction,
parallel to the ramp.
 If we ignore friction, and substitute Newtons' 2nd Law,
the net force is:
Fx = m g sin θ
a= F
m
7.3 Acceleration on a Ramp
 To account for friction, the horizontal component of
acceleration is reduced by combining equations:
Fx = mg sin θ - m mg cos θ
7.3 Acceleration on a Ramp
 For a smooth surface, the coefficient of friction (μ) is
usually in the range 0.1 - 0.3.
 The resulting equation for acceleration is:
7.3 Calculate acceleration on a ramp
 A skier with a mass of 50 kg is on a hill making an angle
of 20 degrees.
 The friction force is 30 N.
 What is the skier’s acceleration?
7.3 Vectors and Direction
Key Question:
How do forces balance
in two dimensions?
*Students read Section 7.3 BEFORE Investigation 7.3
Application: Robot Navigation