Download ppt - Desy

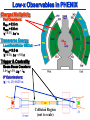
Low-x Observables at RHIC
(with a focus on PHENIX)
Prof. Brian A Cole
Columbia University
Outline
1.
2.
3.
4.
5.
Low-x physics of heavy ion collisions
PHENIX Et and multiplicity measurements
PHOBOS dn/d measurements
High-pt hadrons: geometric scaling ??
Summary
Relativistic Heavy Ion Collider
STAR
Run 1 (2000) : Au-Au
@ SNN = 130 GeV
Run 2 (2001-2): Au-Au, p-p @ SNN = 200 GeV
(1-day run): Au+Au
@ SNN = 20 GeV
Run 3 (2003): d-Au, p-p @ SNN = 200 GeV
Collision seen in “Target” Rest Frame
Projectile boost   104.
 Due
to Lorentz contraction
gluons overlap longitudinally
 They
combine producing large(r)
kt gluons.
Apply uncertainty princ.
 E
= kt2 / 2Px ~  / 2 t
Some numbers:
 x  10-2
 Nuclear crossing t ~ 10 fm/c
 mid-rapidity
 kt2 ~ 2 GeV2
Gluons with much lower kt
are frozen during collision.
Target simply stimulates
emission of pre-existing gluons
How Many Gluons (rough estimate) ?
 Measurements of transverse energy
( Et =  E
sin) in “head on” Au-Au collisions give dEt / d ~ 600
GeV (see below).
 Assume primordial gluons carry same Et
 Gluons created at proper time  and rapidity y
appear at spatial z =  z =  sinh y

So dz =  cosh y dy

In any local (long.) rest frame z =  y.
 dEt / d3x = dEt / d / A (neglecting y,  difference)

For Au-Au collision, A =  6.82  150 fm2.
 Take  = 1/kt , dEt ~ kt dNg
 dNg /d3x ~ 600 GeV/ 150 fm2 / 0.2 GeV fm = 20 fm-3
 For kt ~ 1 GeV/c, dNg / dA ~ 4 fm-2
 Very large gluon densities and fluxes.
“Centrality” in Heavy Ion Collisions
Spectators
Impact parameter
(b)
 Violence of collision determined by b.
 Characterize collision by Npart :
#
of nucleons that “participate” or scatter in collision.
 Nucleons
A
that don’t participate we call spectators.
= 197 for Au  maximum Npart in Au-Au is 394.
 Smaller b  larger Npart , more “central” collisions
 Use Glauber formalism to estimate Npart for
experimental centrality cuts (below).
Saturation in Heavy Ion Collisions
Kharzeev, Levin, Nardi Model
 Large gluon flux in highly boosted nucleus
 When probe w/ resolution Q2 “sees”
multiple partons, twist expansion fails
 i.e.
when  >> 1
 New
scale: Qs2  Q2 at which  = 1
 Take cross section  =  s(Q2) / Q2
 Gluon area density in nucleus   xG(x, Q2) nucleon
 Then solve: Qs2 = [constants] s (Qs2) xG(x, Qs2) nucleon
 Observe:
Qs depends explicitly on nucleon
 KLN obtain Qs2 = 2 GeV2 at center of Au nucleus.
 But gluon flux now can now be related to Qs

 Qs2 / s (Qs2)
Saturation Applied to HI Collisions
 Use above approach to determine gluon flux in
incident nuclei in Au-Au collisions.
 Assume constant fraction, c, of these gluons are
liberated by the collision.
 Assume parton-hadron duality:
 Number
of final hadrons  number of emitted gluons
 To evaluate centrality dependence:
 nucleon 
 Only
½ part
count participants from one nucleus for Qs
 To evaluate energy dependence:
 Take
Qs s dependence from Golec-Biernat & Wüsthof
 Qs(s) / Qs(s0) = (s/s0)/2,  ~ 0.3.
 Try to describe gross features of HI collisions
 e.g.
Multiplicity (dN/d), transverse energy (dEt / d)
Low-x Observables in PHENIX
Charged Multiplicity
Pad Chambers:
RPC1 = 2.5 m
RPC3 = 5.0 m
||<0.35, =
Transverse Energy
Lead-Scintillator EMCal:
REMC = 5.0 m
||<0.38,  = (5/8)
Trigger & Centrality
Beam-Beam Counters:
3.0<||<3.9,  = 2
0º Calorimeters:
|| > 6, |Z|=18.25 m
Collision Region
(not to scale)
PHENIX Centrality Selection
 Zero-degree calorimeters:
ET
 Measure
energy (EZDC)
in spectator neutrons.
 Smaller
EZDC
b
b  smaller EZDC
QBBC
Nch
 Except
@ large b neutrons
carried by nuclear fragments.
 Beam-beam counters:
multiplicity (QBBC)
in nucleon frag. region.
 Smaller
b  larger QBBC
 Make cuts on EZDC vs QBBC
according to fraction of tot
“above” the cut.
 State centrality bins by
fractional range of tot

E.g. 0-5%  5% most central
EZDC
 Measure
15%
20%
5%
10%
QBBC
Charged Particle Multiplicity Measurement
Count particles on statistical basis

Turn magnetic field off.

Form “track candidates” from
hits on two pad chambers.

Require tracks to point to
beamline and match vertex
from beam-beam detector.
 Nchg 
number of such tracks.

Determine background from
false tracks by event mixing

Correct for acceptance,
 conversions, & hadronic
interactions in material.

Show multiplicity distributions
for 0-5%, 5-10%, 10-15%,
15-20% centrality bins
compared to minimum bias.
Minimum bias
0-5%
PHENIX: Et in EM Calorimeter
 Definition: Et =  Ei sini
Sample M Minv Dist.
 Ei
= Eitot - mN for baryons
 Ei = Eitot +mN for antibaryons
 Ei = Eitot for others
 Correct for fraction of
deposited energy
 100%
for , 0, 70 % for 
 Correct for acceptance
 Energy calibration by:
 Minimum
 electron
 0
ionizing part.
E/p matching
mass peak
 Plot Et dist’s for 0-5%, 5-10%,
10-15%, 15-20% centrality bins
compared to minimum bias.
0
dNchg/d (GeV)
per part. pair
dEt/d (GeV)
per part. pair
Et and Nchg Per Participant Pair
Beware of
suppressed zero !
200 GeV
130 GeV
PHENIX preliminary
200 GeV
130 GeV
PHENIX preliminary
Npart
 Bands (bars) – correlated (total) syst. Errors
 Slow change in Et and Nchg per participant pair
 Despite 20 change in total Et or Nchg
Npart
Et Per Charged Particle
 Centrality dependence
of Et and Nchg very
similar @ 130, 200 GeV.
 Take ratio: Et per charged
particle.

perfectly constant
 Little or no dependence
on beam energy.
 Non-trivial given s
dependence of hadron
composition.
 Implication:
 Et /
Nchg determined by
physics of hadronization.
 Only
one of Nchg, Et can
be saturation observable.
PHENIX preliminary
Multiplicity: Model Comparisons
dNchg / d per part. pair
130 GeV
HIJING
200 GeV
X.N.Wang and M.Gyulassy,
PRL 86, 3498 (2001)
Mini-jet
S.Li and X.W.Wang
Phys.Lett.B527:85-91 (2002)
EKRT
K.J.Eskola et al,
Nucl Phys. B570, 379 and
Phys.Lett. B 497, 39 (2001)
KLN
Npart
Npart
D.Kharzeev and M. Nardi,
Phys.Lett. B503, 121 (2001)
D.Kharzeev and E.Levin,
Phys.Lett. B523, 79 (2001)
 KLN saturation model well describes dN/d vs Npart.

Npart variation due to Qs dependence on part (nucleon).
 EKRT uses “final-state” saturation – too strong !!
 Mini-jet + soft model (HIJING) does less well.

Improved Mini-jet model does better.
Introduces an Npart dependent hard cutoff (p0)
Ad Hoc saturation ??
Nchg (200) / Nchg (130)
Multiplicity: Energy Dependence
Npart
 s dependence an important test of saturation
 Determined
by s dependence of Qs from HERA data
 KLN Saturation model correctly predicted the
change in Nchg between 200 and 130 GeV.
 And
the lack of Npart dependence in the ratio.
 Compared to mini-jet (HIJING) model.
dN/d Measurements by PHOBOS
 PHOBOS covers large  range w/ silicon detectors
=-ln tan /2
simulation
Total Nchg (central collision)
 5060 ± 250 @ 200 GeV

 4170 ± 210 @ 130 GeV
 1680 ± 100 @ 19.6 GeV
-5.5
-3
0

+3
+5.5
Kharzeev and Levin
Phys. Lett. B523:79-87, 2001
Additional model “input”
 x dependence of G(x)
outside saturation region
xG(x) ~ x- (1-x)4
 GLR formula for inclusive
gluon emission:

To evaluate yield when one
of nuclei is out of saturation.
 Assumption of gluon mass
(for y  )

M2 = Qs • 1 GeV
 Compare to PHOBOS data
at 130 GeV.
 Incredible agreement ?!!
dN/d

dN/d per part. pair
dN/d Saturation Model Comparisons
Classical Yang-Mills Calculation
Krasnitz,Nara,Venugopalan
Nucl. Phys. A717:268, 2003
 Treat initial gluon fields as
classical fields using M-V
initial conditions.
 Solve classical equations of
motion on the lattice.
 At late times, use harm.
osc. approx. to obtain
gluon yield and kt dist.
 Results depend on input
saturation scale s.



Re-scaled to compare to data.
No absolute prediction
But centrality dependence of
Nchg and Et reproduced.
 But Et /Nchg sensitive to s.
x 2.4
x 1.1
Saturation & Bottom-up Senario
 BMSS start from ~ identical
assumptions as KLN but
 Qs
(b=0)  0.8 GeV.
 Argue
that resulting value
for c, ~ 3, is too large.
 Then evaluate what happens
to gluons after emission
 In
particular, gluon
splitting, thermalization.
 Nchg
no longer directly
proportional to xG(x,Qs)
 Extra factors of s
 Agrees with (PHOBOS) data.

Faster decrease at low Npart
than in KLN (?)
 More reasonable c, c < 1.5
Baier, Mueller, Schiff, and Son
Phys. Lett. B502:51, 2001.
Baier, Mueller, Schiff, and Son
Phys. Lett. B539:46-52, 2002
High-pt Hadron Production
PHENIX 0 pt spectra
Ratio: Measured/expected
Points: data, lines: theory
No dE/dx
Expected
Observed
with dE/dx
 High-pt hadron yield predicted to be suppressed in heavy
ion collisions due to radiative energy loss (dE/dx).
 Suppression observed in central Au-Au data

 x 5 suppression for pt > 4 GeV
 Consistent with calculations including dE/dx.
 What does this have to do with low x ? …
Geometric Scaling @ RHIC ?
Argument
 Geometric scaling
extends well above Qs
 May influence pt
spectra at “high” pt
 Compare saturation
to pQCD at 6, 9 GeV/c
 Saturation
x3 lower in
central collisions.
 Partly responsible for
high-pt suppression ?
 Testable prediction:
 Effect
½ as large
should be seen in
d-Au collisions.
 Data
in few months …
Kharzeev, Levin, McLerran
(hep-ph/0210332)
Yield per participant pair
pQCD
saturation
Summary
 Saturation models can successfully describe
particle multiplicities in HI collisions at RHIC.
 With
few uncontrolled parameters: Qs(s0), c.
 Closest thing we have to ab initio calculation
 They provide falsifiable predictions !
 Connect RHIC physics to DIS observables:
 s
dependence of dN/d  saturation in DIS .
 Geometric scaling  high pt production @ RHIC
 Already going beyond simplest description

e.g. bottom-up analysis.
 But, there are still many issues (e.g.):
 What
is the value for Qs ? Is it large enough ?
 Is Qs really proportional to part (A1/3)?
 How is dn/d related to number of emitted gluons ?
 How do we conclusively decide that saturation
applies (or not) to initial state at RHIC ?