Download PPT - LSU Physics

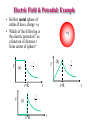
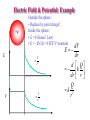
Physics 2102
Jonathan Dowling
Physics 2102
Lecture 6
Electric Potential II
Example
qi
V  k
ri
i
Positive and negative charges of equal
magnitude Q are held in a circle of radius R.
1. What is the electric potential at the center
of each circle?
• VA = k 3Q  2Q /r  kQ/r
• VB = k 2Q  4Q /r  2kQ/r
• VC = k 2Q  2Q  / r  0
 2. Draw an arrow representing the
approximate direction of the electric field at
the center of each circle.
3. Which system has the highest electric
potential energy?
UB
–Q
+Q
A
B
C
Electric Potential of a Dipole (on axis)
What is V at a point at an axial distance r away from the
midpoint of a dipole (on side of positive charge)?
V k
Q
k
Q
a
a
(r  )
(r  )
2
2
a
a 

 (r  2 )  (r  2 ) 
 kQ 

a
a
 (r  )(r  ) 
2
2 

Qa

2
a
2
40 (r  )
4
a
-Q +Q
r
Far away, when r >> a:
V 
p
40 r 2
Electric Potential on Perpendicular
Bisector of Dipole
You bring a charge of Qo = –3C
from infinity to a point P on the
perpendicular bisector of a dipole
as shown. Is the work that you do:
a) Positive?
b) Negative?
c) Zero?
U= QoV=Qo(–Q/d+Q/d)=0
a
-Q +Q d
P
-3C
Continuous Charge
Distributions
• Divide the charge
distribution into
differential elements
• Write down an expression
for potential from a typical
element — treat as point
charge
• Integrate!
• Simple example: circular
rod of radius r, total
charge Q; find V at center.
r
dq
dq
V  k
r
k
Q
  dq k
r
r
Potential of Continuous Charge
Distribution: Example
•
•
•
•
Uniformly charged rod
Total charge Q
Length L
What is V at position P
shown?
x
P
dx
L
a
 Q/L
dq   dx
kdq
kdx
V 

r
(
L

a

x
)
0
L
 k  ln(L  a  x)
L
0
L  a
V  k ln 

 a 
Electric Field & Potential:
A Simple Relationship!
Focus only on a simple case:
electric field that points
along +x axis but whose
magnitude varies with x.
Notice the following:
• Point charge:
– E = kQ/r2
– V = kQ/r
dV
Ex  
dx
• Dipole (far away):
– E ~ kp/r3
– V ~ kp/r2
• E is given by a DERIVATIVE
of V!
f
• Of course! V   E  ds

i
Note:
• MINUS sign!
• Units for E -VOLTS/METER (V/m)
Electric Field & Potential: Example
• Hollow metal sphere of
radius R has a charge +q
• Which of the following is
the electric potential V as
a function of distance r
from center of sphere?
V
1

r
(a)
V
r
r=R
V
+q

(c)
r=R
(b)

r=R
1
r
r
1
r
r
Electric Field & Potential: Example
+q
E
V
Outside the sphere:
• Replace by point charge!
Inside the sphere:
• E =0 (Gauss’ Law)
• E = –dV/dr = 0 IFF V=constant
1
 2
r

1
r
dV
E
dr
d  Q
  k 
dr  r 
Q
k 2
r
Equipotentials and Conductors
• Conducting surfaces are
EQUIPOTENTIALs
• At surface of conductor, E is
normal to surface
• Hence, no work needed to move a
charge from one point on a
conductor surface to another
• Equipotentials are normal to E, so
they follow the shape of the
conductor near the surface.
Conductors change the field
around them!
An uncharged conductor:
A uniform electric field:
An uncharged conductor in the
initially uniform electric field:
“Sharp”conductors
• Charge density is higher at
conductor surfaces that have
small radius of curvature
• E = s/0 for a conductor, hence
STRONGER electric fields at
sharply curved surfaces!
• Used for attracting or getting rid
of charge:
– lightning rods
– Van de Graaf -- metal brush
transfers charge from rubber belt
– Mars pathfinder mission -tungsten points used to get rid of
accumulated charge on rover
(electric breakdown on Mars
occurs at ~100 V/m)
(NASA)
Summary:
• Electric potential: work needed to bring +1C from infinity; units = V
• Electric potential uniquely defined for every point in space -independent of path!
• Electric potential is a scalar -- add contributions from individual point
charges
• We calculated the electric potential produced by a single charge:
V=kq/r, and by continuous charge distributions : V= kdq/r
• Electric field and electric potential: E= dV/dx
• Electric potential energy: work used to build the system, charge by
charge. Use W=qV for each charge.
• Conductors: the charges move to make their surface equipotentials.
• Charge density and electric field are higher on sharp points of
conductors.