* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download PPT - LSU Physics
Magnetic monopole wikipedia , lookup
Electromagnetism wikipedia , lookup
History of electromagnetic theory wikipedia , lookup
Introduction to gauge theory wikipedia , lookup
Electrical resistivity and conductivity wikipedia , lookup
Maxwell's equations wikipedia , lookup
Field (physics) wikipedia , lookup
Potential energy wikipedia , lookup
Lorentz force wikipedia , lookup
Aharonov–Bohm effect wikipedia , lookup
Physics 2113
Jonathan Dowling
Physics 2113
Lecture: 14 FRI 26 SEP
Electric Potential III
Conservative Forces, Work, and Potential Energy
W=
ò F (r)dr
Work Done (W) is
Integral of Force (F)
U = -W
Potential Energy (U)
is Negative of Work
Done
dU
F ( r) = dr
Hence Force is
Negative Derivative
of Potential Energy
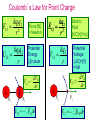
Coulomb’s Law for Point Charge
kq1q2
F12 = 2
r
Force [N]
= Newton
kq1q2
U12 =
r
Potential
Energy
[J]=Joule
dU12
F12 = dr
q2
q1
P2
P1
U12 = - ò F12 dr
Electric
Field
[N/C]=[V/m]
kq2
V12 =
r
Potential
Voltage
[J/C]=[V]
=Volt
dV12
E12 = dr
q2
P2
P1
V12 = - ò E12 dr
Continuous Ring of Charge
• Divide the charge distribution into
differential elements
• Write down an expression for
potential voltalge from a typical
element — treat as point charge
r
dq
• Integrate!
• Simple example: circular rod of
radius r, total charge Q; find V at
center.
Same result
holds along zaxis!
kdq
r
V=
ò dV = ò
k
=
r
k
ò dq = r Q
éNm2 C ù éNmù é J ù
Units : ê 2
ú = ê ú = ê ú º [V ]
ë C mû ë C û ë C û
Potential Voltage of Continuous Charge
Distribution: Return of the Rod!
•
•
•
•
Uniformly charged rod
Total charge +Q
Length L
What is V at position P?
l =Q/ L
kdq
V= ò
=
r
ro d!
dq = l dx
L+a
ò
a
kl dx
x
= kl [ - ln(x)]a
L+a
r=x
P
dq
a
L
dq
éL + aù
V = kl ln ê
ë a úû
Units: [Nm2/C2][C/m]=[Nm/C]=[J/C]=[V]
Potential Voltage of Continuous Charge
•
•
•
•
Uniformly charged rod
Total charge +Q
Length L
What is V at position P?
r = x2 + d 2
l =Q/L
dq = l dx
Electric Field & Potential:
A Simple Relationship!
Notice the following:
• Point charge:
E = kQ/r2
V = kQ/r
• Dipole (far away):
E = kp/r3
V = kp/r2
• E is given by a DERIVATIVE of V!
• Of course!
Focus only on a simple
case: electric field that
points along +x axis but
whose magnitude varies
with x.
dV
Ex = dx
Note:
• MINUS sign!
• Units for E:
VOLTS/METER (V/m)
E from V: Example
• Uniformly charged
rod
• Total charge +Q
• Length L
• We Found V at P!
• Find E from V?
x
dq
L
Units:
a
l =Q/ L
é L + aù
V = kl lnê
ë a úû
= kl{ln[ L + a] - ln[ a]}
dV
d
E== -kl { ln [ L + a ] - ln [ a ]}
da
da
P
1 ü
ì1
= kl í ý
îa L + a þ
éNm2 C m ù éN ù éV ù
=
=
ê 2
2ú ê ú ê ú
ë C m m û ë C û ë mû
√ Electric Field!
Electric Field & Potential: ICPP
•
•
+
Hollow metal spherical shell of
radius R has a charge on the
shell +q
Which of the following is the
electric potential voltage V as a
function of distance r from
center of sphere?
V
+
+
+
r
(b)
»
r=R
1
»
r
r=R
+
V
r=R
(c)
R
+
+
1
»
r
(a)
V
+
r
1
r
r
dV
DV
Ex =
@
(exact for constant field)
dx
Dx
(a) Since Δx is the same, only |ΔV| matters!
|ΔV1| =100, |ΔV2| =180, |ΔV3| =200
|E2| > |E3| > |E1|
The bigger the voltage drop the stronger the field.
Δx
+
+
+
+
-
+
+
+
+
-
(b) = 3
(c) F = qE = ma
+
+
+
+
-
-
accelerate leftward
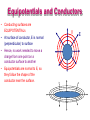
Equipotentials and Conductors
• Conducting surfaces are
EQUIPOTENTIALs
• At surface of conductor, E is normal
(perpendicular) to surface
• Hence, no work needed to move a
charge from one point on a
conductor surface to another
• Equipotentials are normal to E, so
they follow the shape of the
conductor near the surface.
V
E
Conductors Change the Field
Around Them!
An Uncharged Conductor:
A Uniform Electric Field:
An Uncharged Conductor in the
Initially Uniform Electric Field:
Sharp Conductors
• Charge density is higher at
conductor surfaces that have small
radius of curvature
• E = 0 for a conductor, hence
STRONGER electric fields at
sharply curved surfaces!
• Used for attracting or getting rid of
charge:
– lightning rods
– Van de Graaf -- metal brush
transfers charge from rubber belt
– Mars pathfinder mission -tungsten points used to get rid of
accumulated charge on rover
(electric breakdown on Mars
occurs at ~100 V/m)
(NASA)
Ben Franklin Invents the Lightning Rod!
LIGHTNING SAFE CROUCH
If caught out of doors during an approaching storm and
your skin tingles or hair tries to stand on end, immediately
do the "LIGHTNING SAFE CROUCH ”. Squat low to the
ground on the balls of your feet, with your feet close
together. Place your hands on your knees, with your head
between them. Be the smallest target possible, and
minimize your contact with the ground.
Summary:
• Electric potential: work needed to bring +1C from infinity; units = V = Volt
• Electric potential uniquely defined for every point in space -- independent of
path!
• Electric potential is a scalar -- add contributions from individual point
charges
• We calculated the electric potential produced by a single charge: V = kq/r,
and by continuous charge distributions :
dV = kdq/r
• Electric field and electric potential: E= -dV/dx
• Electric potential energy: work used to build the system, charge by charge.
Use W = U = qV for each charge.
• Conductors: the charges move to make their surface equipotentials.
• Charge density and electric field are higher on sharp points of conductors.