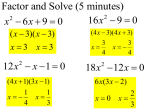Download Unit 4: Complex Numbers

Unit 4: Complex Numbers
Imaginary and Complex Numbers
Objectives:
D.1 To define and illustrate complex numbers.
D.2 To express complex numbers in the form a + bi.
D.3 To add and subtract complex numbers.
D.4 To multiply and divide complex numbers.
D.5 To divide complex numbers using conjugates.
Notes:
To mathematicians, the idea that “you can’t do that” signals a great new challenge. In
many instances we can be faced with a problem such as;
x2 = -16.
The solution to this equation; x = 16 would be simple except for the fact that one can not
find the square root of a negative number. This is clearly a challenge.
We can use the properties of radicals the reduce the problem;
x  16  16  1  4 1
Clever mathematicians such as the 16th century Italians Gerolamo Cardano and Rafael
Bombelli found ways to us the square of numbers such as ( 16 )2 = -16 to get around this
problem. Although they were dismayed by the idea that the square of an impossible number
could be a real number.
René Descartes (of Cartesian plane fame) finally formalized the idea of an imaginary
number whose square is -1. Today we symbolize it as i  1
Once we have the idea of an imaginary number equal to the square root of -1, we can
determine some of its properties:
If i = 1 , then
i2 = ( 1 )2 = -1
i3 = ( 1 )2× 1 = -1× 1 = - 1
i4 = ( 1 )2( 1 )2 = (-1)(-1) = 1
etc.
Also; 81 =
or; 96 =
81  1 = 9i
96  1 = 16  6  1 = 4 6i
Unit 4: Complex Numbers
Often enough to be embarrassing, we find that the solution to an equation (such as a
quadratic) ends up having an imaginary component. These numbers, usually written z = a +
bi where a, and b are real numbers, are known collectively as Complex Numbers.
The mathematics of complex numbers are an extension of the mathematics of radicals:
1.-Any square root of any negative number can be reduced to
x  1 or
xi
2.-Addition and subtraction of complex numbers is carried out by adding “like” to “like”.
For example; (2 + 3i) + (7 - 5i) = 9 - 2i.
3.-Multiplication of complex numbers uses the distributive property.
For example; 3(1 - 4i) = 3•1 - 3•4i = 3 - 12i
or; (2 + 3i)(1 - 5i) = 2•1 - 2•5i + 3i•1 - 3i•5i = 2 - 10i + 3i - 15i2 = 2 - 7i - 15i2
Except: i2 = -1
Therefore: 2 - 7i - 15i2 = 2 - 7i -15(-1) = 17 - 7i
4.-When dividing by complex numbers it is a requirement that i does not remain in the
denominator. (Recall “rationalizing the denominator” in earlier classes.)
For Example:Simplify;
a. 12
c. 18  8
Solution: a.
12  12  1  4  3  i  2i 3
 36  72  36  1  72  1

 6i  36  2  i

b. 
 6i  6i 2


 (1  2)6i

 18  8  18  1  8  1


 144  i 2
c. 
 12  (1)


 12

d.
15
15
3 i i 3 i 3


  2 
 i 3
i i
i
1
5 i 5
-96-
b.
36  72
d.
15
5
Unit 4: Complex Numbers
Notice that the first step in the simplification is to remove the factor of 1  i from the
radical. In question d. this was done in one step.
It is convenient to start most questions this way:  x  i x
In questions c. and d. we made use of the property that i2 = -1.
i
In question d. we rationalized the denominator by multiplying by .
i
For Example: Complete the following operations;
a. 5 + 25
c. 3i(8 - 6i)
e. (12 + 15i) ÷ 3i
Solutions: a. 5 +
b. 3(5 + 2i)
d. (4 - 2i) - (5 - 3i)
25 = 5 + i 25 = 5 + 5i
Note: 5 and 5i are not “like terms”.
b. 3(5 + 2i) = 3×5 + 3×2i = 15 + 6i
Distributive property.
c. 3i(8 - 6i) = 24i - 18i2 = 24i - 18(-1) = 24i + 18 = 18 + 24i
a + bi = standard form
d. (4 - 2i) - (5 - 3i) = 4 - 2i - 5 + 3i = -1 + i
e. (12 + 15i) ÷ 3i
Simplify and rationalize the denominator.
2
12  15i 4  5i i 4i  5i
4i  5


 

 5  4i
2
3i
i
i
i
1
Practice Questions 1: Imaginary and Complex Numbers
1. Evaluate:
a. 64
c. i5
e. 4i9
b. i3
d. 12  3
f. 3  27
2. What is the rule for simplifying powers of i? Hint: try i2, i3, i4, i5, i6, i7, i8, etc
3. Simplify:
a. 125
c. 5 36
b. 3 72
d. (i 5) 2
e. 36  9
f. 3 72  98
g. i 2  i 18
h. 3i 2
i.

32
2
j.
-97-
9
27

2
Unit 4: Complex Numbers
23
i
24  6i
m.
36
o. 4(5 - 3i)
q. (3 + 2i) + (5 - 4i)
k.
l.
50  5i
n.
32  8
p. (2 + 6i) - (1 + 7i)
r. 3i(2 - 5i) + (-3 + 4i)
4. Solve;
a. x2 + 36 = 0
c. 5x2 = -180
b. y2 + 400 = 0
d. (x + 3)2 = -4
Multiplication of Complex Numbers
The standard form for a complex number is a + bi, where a & b are real numbers. This is
very similar in form to binomials. Consequently, many operations with complex numbers are
the same as for binomials with the exception that powers of it can be further simplified.
For Example: Simplify the following;
a. (3 - i)2
c. (2 + i)(3 - 2i)(2 - 2i)
b. (2 + 3i)(4 - 2i)
Solutions: a. (3 - i)2 = (3 - i)(3 - i)
= 9 - 3i - 3i + i2
= 9 -6i - 1
= 8 - 6i
Using F.O.I.L.
i2 = -1
b. (2 + 3i)(4 - 2i) = 8 - 4i + 12i - 6i2 = 8 + 8i -(-6) = 14 + 8i
c. (2 + i)(3 - 2i)(2 - 2i)
= (6 - 4i + 3i - 2i2)(2 - 2i)
= (6 + i - (-2))(2 - 2i)
= (8 + i)(2 - 2i)
= 16 - 16i + 2i - 2i2
= 16 - 14i + 2
= 18 - 14i
Practice Questions 2: Multiplying Complex Numbers
1. Simplify;
a. (2 + 3i)(4 - 2i)
c. 2  3i 1  4i
b. (-5 + 3i)(2 - 7i)
d. 2i(3 + 2i)(3 + 3i)



e.  3  i 3   4  i 
f. 2(1 - 6i) + 3(2 - 4i)
g. (-3 + i)2
h. (2 + 4i)3
i. (3 + 2i)(3 - 2i)
j. 3  i 3

-98-

2
 2  3i  2  3i 
m.  1  i 3 
k.
Unit 4: Complex Numbers
l. (2 - i)3(2 + i)3
3
 2 i 2
o. 


2 
 2
n.

3  5

3  5

2
Division of Complex Numbers
In the previous set of practice questions, you may have noticed that in certain situations a
product of complex numbers can be a real number. Specifically, any product of the form;
(a + bi)(a - bi)
These numbers are called conjugates. For example: the conjugate of 3 + 7i is 3 - 7i. We
can use conjugates to rationalize the denominator of complex quotients;
For Example: Divide;
3
a.
2  4i
2  i 3
c.
2  i 3
b.
2  3i
3  2i
3
3
2  4i 6  12i 6  12i 6  12i 3 3i





 
2  4i 2  4i 2  4i 4  16i 2 4  16
20
10 5
2
2
2  3i 2  3i 3  2i 6  13i  6i
6  13i  6 13i
b.





i
2
3  2i 3  2i 3  2i
9  4i
94
13
Solution: a.
c.
2  i 3 2  i 3 2  i 3 4  4i 3  3i 2 1  4i 3 1 4i 3




 
4  3i 2
7
7
7
2  i 3 2  i 3 2  i 3
Notice that the answer is always put into the form a + bi.
The conjugate is also useful in determining the absolute value of a complex number:
|a + bi|2 = (a + bi)(a - bi) or |a + bi| =
 a  bi  a  bi 
For Example: Find |2 - 3i|
Solution: |2 - 3i| =
 2  3i  2  3i  
4  9i 2  13 =
-99-
4  9 i
2
=
13
Unit 4: Complex Numbers
Practice Questions 3: Division of Complex Numbers.
1. Simplify the following: (rationalize the denominators.)
a. 7 ÷ i
b. 12 ÷ 3i
16  8i
(3  2i )(5  3i)
c.
d.
4i
7i
36
12
e.
f.
2  3i
2i
1
1
g.
h.
a  bi
5 i
i.
3 i 2
3 i 2
j.
2. Calculate the absolute value;
a. |3 - 4i|
c. 6  i 5
2i 3
2  i 3
2
5– 5
1
2
3
4
1
2
3
4
1– 5
2
3
4
5
1
2
3
4
b. |12 + 5i|
d. |9 - 5i|
The Complex Coordinate Plane
i
5
It is sometimes useful to represent complex
numbers on the Argand-Gauss coordinate
plane, a coordinate system similar to the
Cartesian plane.
4
3
2
1
For Example: The complex number 5 + 3i can
1– 1
2
3
4
5
6
7
8
be represented. Using the diagram87654321to
– 1the right.
– 5– 4– 3– 2– 1
– 1
1
2
3
4
5
x
– 2
– 3
– 4
– 5
When represented this way, several features of the complex number are readily apparent;
i
1. The number has two components, the real
component represented on the horizontal
8
axis, and the imaginary component on the
7
vertical axis.
Result = 8 + 6i
6
4i
5
3+
When complex numbers are added, the
real components are added together and the
imaginary components are added together;
4
3
2
Example:
(5 + 3i) + (3 + 4i) = (5 + 3) + (2i + 4i)
= 8 + 6i
5+
1
– 1
– 1
-100-
1
2
2I
3
4
5
6
7
8
x
8– 1
1
2
3
4
5
6
7
1– 1
2
3
4
5
6
7
8
6i
Unit 4: Complex Numbers
2. The Absolute Value or Magnitude of the complex number is the distance from the origin to
the location of the point on the coordinate plane.
We can use Pythagoras’ theorem to calculate the absolute value.
i
In the diagram to the right, we can see that
|z|
is
the hypotenuse of a right triangle. Using
8
Pythagoras we can calculate;
7
6
5
4
|8
+
=
6i|
|z|2 = 62 + 82 = 36 + 64 = 100
|z| = 100 10 0 = 10
|
|z
3
In general for a complex number of the form;
6i
2
1
z = a + bi,
8
– 1
– 1
1
2
3
4
5
6
7
|z| =
a 2  b2
x
8
Practice Questions 4: The Complex Plane
1. Illustrate the following on the Complex Coordinate Plane;
a. 3 + 4i
c. 5 - 6i
e. |4 - 3i|
b. -2 + 3i
d. (3 + 2i) + (2 - 4i)
f. (-2 + 5i) - (-4 + 3i) hint:add the opposite
2. Given the general form of a complex number, prove that our two formulae for the absolute
value are equivalent:
If z = a + bi, then
(a  bi )(a  bi )  a 2  b 2
Unit 4: Solutions
Practice Questions 1: page 91
1. a. 8i
b. -i
c. i
d. 6i
e. 4i
f. -9
2. One can divide powers of i into groups of i4 = 1, i2 = -1, and i.
For example i45 = (i4)11•i = (1)11•i = 1i = i
3. a. 5i 5 b. 18i 2 c.-30i d. -5 e. 3i f. 25i 2 g. -6i h. 54 2
j. i 3 k. -23i l. 2 m. -1 + 4i n. 84i 2 o. 20 - 12i p. 1 - i
q. 8 - 2i r. 12 + 10i
4. a. x = ±6i
b. y = ±20i
c. x = ±6i
d. x = -3 ± 2i
Practice Questions 2: Page 92
-101-
i. 4i
Unit 4: Complex Numbers
1. a. 14 + 8i b. 11 + 41i c. 107i 2 d. -30 + 6i e. 12  3i  4i 3  3
f. 10 - 24i g. 8 - 6i h. -88 - 16i i. 13 j. 6  6i 3 k. 11 l. 125 m. 8
n. 2 o. i
Practice Questions 3: Page 93
1. a. -7i
g.
b. -4i
5 i

6 6
c. 2 - 4i
a  bi
h.
a 2  b2
d. 1/7 - 3i

e.
24  12i 24 12

 i
5
5 5
(a  bi) a 2  b2
a 2  b2
8– 1
1
2
3
4
5
6
7
1– 1
2
3
4
5
6
7
8
1 2i 6
i. 
5
5
f.
j. 
12  2 3  18i  3i 3
11
10 5i 3

13 13
5– 5
1
2
3
4
1
2
3
4
1– 5
2
3
4
5
1
2
3
4
2. a. 5
b. 13
c. 11
d. 106
Practice Questions 4: Page 95
1.
i
a.
i
b.
5
8
4
7
-2
3
6
5– 5
1
2
3
4
1
2
3
4
1– 5
2
3
4
5
1
2
3
4
3+
4i
3
2
– 5– 4– 3– 2– 1
– 1
1
2
3
4
5
6
7
x
8
3
4
2
3
4
5
x
– 4
– 5
i
c.
i
d.
3
5
2
4
1
3
1
2
4
5
6
7
2
x
2i
3+
1
i
– 5
5–
1
2
3
4
12 + 5i– ( – 4 + 3i –= 54––43i– 3 – 2 – 1
2
3
4
1– 5
2
3
4
5
1
2
3
4
– 1
5
– 2
– 3i
1–
1
2
3
4
5
1z– 1= 42 + ( – 3)2 = 25 = 5 – 3
2
3
4
5
3
2-4
– 3– 2– 1
– 1
i
-6
– 4
– 2
– 5
– 3
– 6
– 4
– 7
1
5
x
Final = 5 - 2i
– 5
i
i
f.
1
5
4
2
1
4-
– 1
3
4
5
x
– 2 + 5i
– ( 4– 4 + 3i = 4 – 3i
3
2
3i
– 3i
– 5– 4– 3– 2– 1
– 1
2
Result= 2 + 2i
1
– 2
– 3
2
– 3
– 1
– 1
– 1
1
– 2
1
e.
3i
1
4
3– 7
1
2
1
2
3
4
5
6
1– 3
2
3
4
5
6
7
1
2
+
2
5
– 2
2
z = 4 + ( – 3) = 25 = 5
– 3
– 4
– 4
– 5
– 5
-102-
1
2
3
4
5
x
Unit 4: Complex Numbers
2. Proof as follows.
?
The statement to be proven
?
Multiplication of (a + bi)(a - bi)
(a  bi )(a  bi )  a 2  b 2
a 2  b 2i 2  a 2  b 2
?
a 2  b 2 (1)  a 2  b 2
a 2  b2  a 2  b2
i2 = -1
Proof complete.
-103-
Unit 4: Complex Numbers
Unit 4 Review
1. In a response to equations such as x 2  25 or x  25 , mathematicians have created the
idea of imaginary numbers based on the number i = 1 .
2. Imaginary numbers can be used to simplify expressions containing the square root of a
negative number by first rewriting the expression using i:
25  i 25  5i
3. A complex number is a number if the form a + bi where a and b are real numbers. “a” is the
real part and “bi” is the imaginary part of the complex number.
4. The mathematics of complex and imaginary numbers is and extension of the mathematics of
radicals:
i.-Any square root of any negative number can be reduced to x  1 or x i
ii.-Addition and subtraction of complex numbers is carried out by adding “like” to “like”.
For example; (2 + 3i) + (7 - 5i) = 9 - 2i.
iii.-Multiplication of complex numbers uses the distributive property.
For example; 3(1 - 4i) = 3×1 - 3×4i = 3 - 12i
Or:
(2 + 3i)(3 - 2i) = 6 - 4i + 9i - 6i2
= 6 + 5i - 6(-1)
= 12 + 5i
iv.- As with radicals, the denominator of any rational must be rationalized. (No i’s
allowed on the bottom of a fraction.) This is achieved by multiplying both numerator and
denominator by the conjugate of 321the
– 7
1 complex number: For a + bi, the conjugate is a - bi.
2
3
4
5
6
1– 3
2
3
4
5
6
7
1
2
5. The absolute value of a complex number can be found in two ways;
For z = a + bi, |z| =
(a  bi )(a  bi )  a 2  b 2
6. Complex numbers may be represented on
the Complex or Argand-Gauss Plane. The
real part is represented on the horizontal axis
and the imaginary part is represented on the
vertical axis
i
3
2
1
– 3– 2– 1
– 1
– 5
– 6
– 7
-104-
4
i
– 4
3
-6
– 3
2
5
– 2
1
5
6
7
x
Unit 4: Complex Numbers
Unit 4 Review Questions
1. Evaluate the following;
a. 121
c. i3
b. 36  9
d. 7i7
144
f.
400
e. (-5i)3
2. Simplify each of the following;
a. 450
c. 3i•5i

e. 3 6

b. 50  18
d. -i(2i)3
2
f. 4(3 - 2i)


3
g. (2 - 5i)(7 + 2i)
h. 1  i 3
i. (2 - 7i) - (3 + 4i)
j. 2(3 - i) - 5(-2 + 3i)
3. Find the conjugate of each of the following;
a. 2 - 3i
c. 3  2i
b. -2i
d. 7 + 3i
4. Simplify each of the following;
a. 12 ÷ 3i
9  3i
c.
3i
6
e.
2i
2
g.
2  3i
b. 15 ÷ 6i
45  25i
d.
15i
2  3i
f.
2  3i
6  3
h.
6  3
5. Calculate the following;
a. |3 - 2i|
c. |11 - 7i|
b. |8 + 6i|
d. 17  i 8
6. Graph each of the following on the complex plane;
a. -3 + 5i
b. 7 - 6i
c. (3 + 2i) + (5 - 7i)
d. |12 + 9i|
7. Solve each of the following;
a. x2 + 36 = 0
c. (x - 3)2 + 121 =0
b. y2 = - 625
-105-
Unit 4: Complex Numbers
Unit 4 Review Questions Solutions
1. a. 11i b. -18
c. -i
d. -7i
2. a. 15i 2 b. 2i 2
3. a. 2 + 3i
4. a. -4i
h.
5– 5
1
2
3
4
1
2
3
4
1– 5
2
3
4
5
1
2
3
4
c.-15
d.-8
c. 3  2i
b. i
b. -3i/2
c. -1 - 3i
e. 125i
e.-54
f.12 - 8i
g. 24 - 31i
h.-8 i. -1 - 3i
j. 16 -17i
d. 7 - 3i
d. -5/3 - 3i
1 2i 2

3
3
5. a. 13
f. 3i/5
e. 12/5 + 6i/5
f. -5/13 + 12i/13
g.
2 3i 2

11 11
1– 8
1
2
3
4
5
6
7
1– 2
2
3
4
5
6
7
1
c. 170
b. 10
d. 5
6.
a.
b.
i
i
5
1
-3
4
– 2– 1
– 1
2
– 2
1
– 3
i
+5
3
3– 7
1
2
1
2
3
4
5
6
1– 1
2
3
4
5
6
7
8
– 5– 4– 3– 2– 1
– 1
1
2
3
4
5
2
3
4
7
5
6
7
x
14
x
-6
i
– 4
9i
2
4
6
8
10
12
14
2
4
6
8
10
12
14
x
1
– 5
– 2
– 6
– 3
– 7
– 4
– 8
– 5
i
c.
i
d.
3
2
1
1
2
12
3
4
5
6
5-
7
8
10
x
7i
– 1
– 1
14
2i
3+
8
– 2
– 4
Result: 8 - 5i
+
12
z=
9
9i
4
– 5
2
– 6
– 7
7. a. x = 6i
|z| = 15i
6
– 3
2
b. y = 25i
c. x = 3 ± 11i
-106-
4
12
6
8
10
12