* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download example 2 - my Mancosa
Data assimilation wikipedia , lookup
Linear regression wikipedia , lookup
Time series wikipedia , lookup
Regression analysis wikipedia , lookup
Least squares wikipedia , lookup
Regression toward the mean wikipedia , lookup
Interaction (statistics) wikipedia , lookup
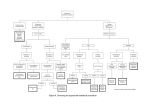
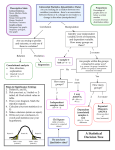
ANSWERS Remember, always ! 1. What are the researchers actually wanting to do? Put it in your own terminology 2. Identify your IV and DV first 3. Determine the level of measurement of you IV and DV 4. Set up your null an alternate hypotheses 5. Determine if p is < 0.05, or > 0.05, then conclude with reference to the scenario 6. Report the statistics in standard reporting format EXAMPLE 1 What kind of data we are dealing with? In the present study, the data type is nominal data. Whether our data follow the normal distribution or not? There is no need to check distribution in nominal data. They follow chi-square distribution. So we can say that most appropriate test in this condition will be 'Fishers Test' (Chi-Square if large sample size). EXAMPLE 2: One-Way ANOVA EXAMPLE 3: When a company wants to compare the employee productivity based on two factors (2 independent variables), then it said to be two way (Factorial) ANOVA. Two way ANOVA. Two-way ANOVA’s can be used to see the effect of one of the factors after controlling for the other, or it can be used to see the INTERACTION between the two factors. This is a great way to control for extraneous variables as you are able to add them to the design of the study. An aside: ** In ANOVA, the dependent variable can be continuous or on the interval scale. Factor variables in ANOVA should be categorical. ** ANOVA assumes that the distribution of data should be normally distributed. ANOVA also assumes the assumption of homogeneity, which means that the variance between the groups should be equal. ANOVA also assumes that the cases are independent to each other or there should not be any pattern between the cases. As usual, when planning any study, extraneous and confounding variables need to be considered. ANOVA is a way to control these types of undesirable variables. ** The assumption of homogeneity of variance can be tested using tests such as Levene’s test or the Brown-Forsythe Test. Normality of the distribution of the population can be tested using plots, the values of skewness and kurtosis, or using tests such as Shapiro-Wilk or Kolmogorov-Smirnov. The assumption of independence can be determined from the design of the study. EXAMPLE 4: Related samples t-test. EXAMPLE 5: Mann-Whitney U EXAMPLE 6: Kruskal-Wallis EXAMPLE 7: Type of Data: Math score and number of hours are both ratio variables Statistical Test: Pearson’s r EXAMPLE 8: Type of Data: Math scores of both Sections A and B are ratio variables. Statistical Test: t-test EXAMPLE 9: z-test EXAMPLE 10: t-test EXAMPLE 11: One-sample t-test EXAMPLE 12: Independent samples t-test **A t-test helps you compare whether two groups have different average values (for example, whether men and women have different average heights). **The “One Sample T-Test” is similar to the “Independent Samples T-Test” except it is used to compare one group’s average value to a single number (for example, do Durbanites on average spend more than R53 per month on movies?). EXAMPLE 13: Kruskal-Wallis **The Kruskal-Wallis H test (sometimes also called the "one-way ANOVA on ranks") is a rank-based nonparametric test that can be used to determine if there are statistically significant differences between two or more groups of an independent variable on a continuous or ordinal dependent variable. It is considered the nonparametric alternative to the one-way ANOVA, and an extension of the Mann-Whitney U test to allow the comparison of more than two independent groups. **Assumption #1: Your dependent variable should be measured at the ordinal or continuous level (i.e., interval or ratio). Examples of ordinal variables include Likert scales (e.g., a 7-point scale from "strongly agree" through to "strongly disagree"), amongst other ways of ranking categories (e.g., a 3pont scale explaining how much a customer liked a product, ranging from "Not very much", to "It is OK", to "Yes, a lot"). Examples of continuous variables include revision time (measured in hours), intelligence (measured using IQ score), exam performance (measured from 0 to 100), weight (measured in kg), and so forth. You can learn more about ordinal and continuous variables in our article: Types of Variable. Assumption #2: Your independent variable should consist of two or more categorical, independent groups. Typically, a Kruskal-Wallis H test is used when you have three or more categorical, independent groups, but it can be used for just two groups (i.e., a Mann-Whitney U test is more commonly used for two groups). Example independent variables that meet this criterion include ethnicity (e.g., three groups: Caucasian, African American and Hispanic), physical activity level (e.g., four groups: sedentary, low, moderate and high), profession (e.g., five groups: surgeon, doctor, nurse, dentist, therapist), and so forth. Assumption #3: You should have independence of observations, which means that there is no relationship between the observations in each group or between the groups themselves. For example, there must be different participants in each group with no participant being in more than one group. This is more of a study design issue than something you can test for, but it is an important assumption of the Kruskal-Wallis H test. If your study fails this assumption, you will need to use another statistical test instead of the Kruskal-Wallis H test (e.g., a Friedman test). If you are unsure whether your study meets this assumption, you can use our Statistical Test Selector, which is part of our enhanced content. EXAMPLE 14: If you using rank (not raw scores) - Kruskal-Wallis Ho : The weight distribution for all four populations are all the same Ha : At least two the population distributions differ in location. EXAMPLE 15: Mann-Whitney U We have two conditions, with each participant taking part in only one of the conditions. The data are ratings (ordinal data), and hence a nonparametric test is appropriate - the Mann-Whitney U test (the nonparametric counterpart of an independent measures t-test). EXAMPLE 16: Linear Regression and Correlation EXAMPLE 17: One-way ANOVA EXAMPLE 18: One-way ANOVA EXAMPLE 19: Chi-Square EXAMPLE 20: One-sample Chi-Square Test ** SPSS one-sample chi-square test is used to test whether a single categorical variable follows a hypothesized population distribution. If you look at the output: P > 0.05, Therefore we fail to reject the null hypothesis and conclude that There is no significant association between cellphone brand, and rated attractiveness (χ² (3) = 6.953, p = 0.073) JUST REMEMBER: MUTUALLY EXCLUSIVE EXHAUSTIVE Check your assumption of more than 5 counts in more than 80% of the cells EXAMPLE 21: One Sample T-Test **The one sample t-test compares the mean of one variable for one group with a given value: was the mean income over 2015 equal to $30,000,-? **The independent samples t test compares the means of one variable for two groups of cases. For example, did men and women have the same mean income over 2015? **The paired samples t-test compares the means of two variables for one group. For example, was the mean income over 2015 the same as the mean income over 2014? EXAMPLE 22: Independent samples t-test EXAMPLE 23: Paired Samples T-Test/Related sample t-test EXAMPLE 24: Pearson Correlation EXAMPLE 25: Simple Linear Regression EXAMPLE 26: Look at the strength, direction, and significance. All correlations are significant, except for Job motivation and IQ, and Social Support and IQ. EXAMPLE 27: The Friedman Test **For testing if 3 or more variables have identical population means, our first option is a repeated measures ANOVA. This requires our data to meet some assumptions -like normally distributed variables. If such assumptions aren't met, then our second option is the Friedman test: a nonparametric alternative for a repeated-measures ANOVA. **Strictly, the Friedman test can be used on metric or ordinal variables but ties may be an issue in the latter case. EXAMPLE 28: One-way ANOVA EXAMPLE 29: Mann-Whitney U Example 30: z-test HO: The mean verbal SAT score for first year MBA students is not significantly different from the mean verbal SAT score for the population of first students at MANCOSA. H1: The mean verbal SAT score for first year MBA students is significantly different from the mean verbal SAT score for the population of first students at MANCOSA. Example 31: t-test Example 32: Independent samples t-test HO: There is no significant difference in scores on Need for Achievement between Type A and Type B participants H1: There is a significant difference in scores on Need for Achievement between Type A and Type B participants Conclusion: P < 0.05, therefore we reject the null hypothesis and conclude that, There is a significant difference in scores on Need for Achievement between Type A and Type B participants (t(18) = 3.735, p = 0.002). Example 33: Positive, moderate, insignificant correlation Example 34: Paired samples t-test Problematic machines are Machine 2, Machine 4, Machine 7 Example 35: We are looking at changes in: 1. Triglyceride levels 2. Weight Related samples/paired samples t-test There has been a change in weight, but not triglyceride levels. Statistics. For each variable: mean, sample size, standard deviation, and standard error of the mean. For each pair of variables: correlation, average difference in means, t test, and confidence interval for mean difference (you can specify the confidence level). Standard deviation and standard error of the mean difference. Paired-Samples T Test Data Considerations Data. For each paired test, specify two quantitative variables (interval level of measurement or ratio level of measurement). For a matched-pairs or case-control study, the response for each test subject and its matched control subject must be in the same case in the data file. Assumptions. Observations for each pair should be made under the same conditions. The mean differences should be normally distributed. Variances of each variable can be equal or unequal. Example 36: Independent samples t-test There is a significant difference in credit card purchases between the two adverts (t(498) = -2.260, p = 0.024). Statistics. For each variable: sample size, mean, standard deviation, and standard error of the mean. For the difference in means: mean, standard error, and confidence interval (you can specify the confidence level). Tests: Levene's test for equality of variances and both pooled-variances and separate-variances t tests for equality of means. Independent-Samples T Test Data Considerations Data. The values of the quantitative variable of interest are in a single column in the data file. The procedure uses a grouping variable with two values to separate the cases into two groups. The grouping variable can be numeric (values such as 1 and 2 or 6.25 and 12.5) or short string (such as yes and no). As an alternative, you can use a quantitative variable, such as age, to split the cases into two groups by specifying a cutpoint (cutpoint 21 splits age into an under-21 group and a 21-and-over group). Assumptions. For the equal-variance t test, the observations should be independent, random samples from normal distributions with the same population variance. For the unequal-variance t test, the observations should be independent, random samples from normal distributions. The twosample t test is fairly robust to departures from normality. When checking distributions graphically, look to see that they are symmetric and have no outliers. Example 37: One-way ANOVA Stop ANOVA - The Levene statistic rejects the null hypothesis that the group variances are equal. ANOVA is robust to this violation when the groups are of equal or near equal size; however, you may choose to transform the data or perform a nonparametric test that does not require this assumption. Example 38: One-way ANOVA Hₒ: There is no significant difference in age and DVD rating Hᵢ: There is a significant difference in age and DVD rating P < 0.05, Therefore we reject the null hypothesis and conclude that There is a significant difference in age and DVD rating (F(5:62) = 6.993, p < 0.0001). If you look at the means plot – you can see the age groups 35-44, and 45-54 years rated the DVD player higher than other age groups. Example 40: Factorial ANOVA The tests of between-subjects effects help you to determine the significance of a factor. However, they do not indicate how the levels of a factor differ. The post hoc tests show the differences in model-predicted means for each pair of factor levels. The first column displays the different post hoc tests. The next two columns display the pair of factor levels being tested. When the significance value for the difference in Amount spent for a pair of factor levels is less than 0.05, an asterisk (*) is printed by the difference. In this case, there do not appear to be significant differences in the spending habits of "biweekly", "weekly", or "often" customers. In this example, the post hoc tests did not reveal a difference in spending between customers who shopped biweekly and those who shopped more often. However, the estimated marginal means and profile plots revealed an interaction between the two factors, suggesting that male customers who shop once a week are more profitable than those who shop more often, while the pattern is reversed for female customers. The significance of this interaction effect was confirmed by the results of the ANOVA table. Example 41: There is no significant correlation between fuel efficiency and price paid for cars in thousands of rands (r = -0.017, N = 154, p = 0.837). Example 42: Linear Regression The ANOVA table reports a significant F statistic, indicating that using the model is better than guessing the mean. As a whole, the regression does a good job of modelling sales. Nearly half the variation in sales is explained by the model. Even though the model fit looks positive, the first section of the coefficients table shows that there are too many predictors in the model. There are several non-significant coefficients, indicating that these variables do not contribute much to the model. To determine the relative importance of the significant predictors, look at the standardized coefficients. Even though Price in thousands has a small coefficient compared to Vehicle type, Price in thousands actually contributes more to the model because it has a larger absolute standardized coefficient. The significant variables include vehicle type, price, and fuel efficiency. Example 43: 1. Independent samples nonparametric tests – Kruskal-Wallis 2. Related samples nonparametric tests- Friedman’s Example 44: Chi-Square: Hₒ: There is no significant association between income level and PDA type owned Hᵢ: There is a significant association between income level and PDA type owned P < 0.05, Therefore we reject the null hypothesis and conclude that There is a significant association between income level and PDA type owned (χ²(3) = 37.677, p < 0.0001).