1 Appendix to notes 2, on Hyperbolic geometry:
... Faces are all regular polyhedra, but they are not all the same polyhedron. Archimedes proved that there are exactly 13 of these. ...
... Faces are all regular polyhedra, but they are not all the same polyhedron. Archimedes proved that there are exactly 13 of these. ...
Mathematical Origami: PHiZZ Dodecahedron
... Now that we know a dodecahedron is composed of 12 pentagon faces and a total of 30 edges, we are ready to make a dodecahedron out of PHiZZ modular origami units. Each PHiZZ unit will form one edge of the dodecahedron so we will need 30 square pieces of paper. (The 3”× 3” memo cube paper from Staples ...
... Now that we know a dodecahedron is composed of 12 pentagon faces and a total of 30 edges, we are ready to make a dodecahedron out of PHiZZ modular origami units. Each PHiZZ unit will form one edge of the dodecahedron so we will need 30 square pieces of paper. (The 3”× 3” memo cube paper from Staples ...
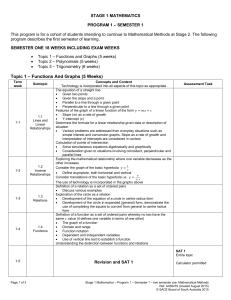
Common Core Math I, II, and III – Summary of Concepts
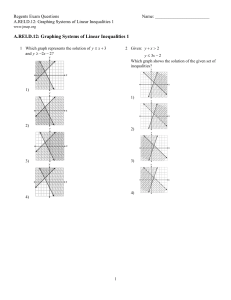
... Solve a system of linear equations by graphing or making a table (I) (A-REI-6) Solve a system of linear equations using algebraic methods (substitution or elimination) (I) (A-REI.5) Solve a linear-exponential system by graphing or making a table (I) (AREI.6) Solve a linear-quadratic system b ...
... Solve a system of linear equations by graphing or making a table (I) (A-REI-6) Solve a system of linear equations using algebraic methods (substitution or elimination) (I) (A-REI.5) Solve a linear-exponential system by graphing or making a table (I) (AREI.6) Solve a linear-quadratic system b ...
Math 2 Updated Objectives and Outcomes
... a. Obtain the different forms of the equation of a linear function. b. Identify from any form of the equation of a line its slope and intercepts. c. Solve application problems involving linear functions. d. Find the zeros of a quadratic function by factoring, by completing the square and by using th ...
... a. Obtain the different forms of the equation of a linear function. b. Identify from any form of the equation of a line its slope and intercepts. c. Solve application problems involving linear functions. d. Find the zeros of a quadratic function by factoring, by completing the square and by using th ...
8-3 Angle Relationships
... two nonvertical lines whose slopes have a product of -1 are perpendicular. Vertical and horizontal lines are perpendicular. ...
... two nonvertical lines whose slopes have a product of -1 are perpendicular. Vertical and horizontal lines are perpendicular. ...
Course Outline
... make fair divisions by dividing an item considered continuous between two or more people make fair divisions by dividing a set of items considered discrete among two or more people ...
... make fair divisions by dividing an item considered continuous between two or more people make fair divisions by dividing a set of items considered discrete among two or more people ...
f(x) - Laurus Online Math Computer Tutor
... (vi , vj ) according to whether or not vi and vj are adjacent. For a simple graph with no selfloops, the adjacency matrix must have zeros on the diagonal while the adjacency matrix for an undirected graph is symmetrical touching at some point or along a line a group of numbers, symbols, and variable ...
... (vi , vj ) according to whether or not vi and vj are adjacent. For a simple graph with no selfloops, the adjacency matrix must have zeros on the diagonal while the adjacency matrix for an undirected graph is symmetrical touching at some point or along a line a group of numbers, symbols, and variable ...
ppt
... Suppose also there is an object I (or objects) which parametrize behaviours: i.e. Hom(I,X) is the set of behaviours of object X. Example 1. E=Graphs. The objects which parametrize motion are the graphs In=0->1->…->n. A behaviour in X is a path in the graph X. Behaviours, by virtue of a famillial coc ...
... Suppose also there is an object I (or objects) which parametrize behaviours: i.e. Hom(I,X) is the set of behaviours of object X. Example 1. E=Graphs. The objects which parametrize motion are the graphs In=0->1->…->n. A behaviour in X is a path in the graph X. Behaviours, by virtue of a famillial coc ...
Separating Doubly Nonnegative and Completely
... • Separation procedure based on transformed Horn matrix applies to X ∈ D5 \ C5 where X has rank three and G(X) has at least one vertex of degree 2. • More general separation procedure applies to any X ∈ D5 \ C5 that is not componentwise strictly positive. An even more general separation procedure th ...
... • Separation procedure based on transformed Horn matrix applies to X ∈ D5 \ C5 where X has rank three and G(X) has at least one vertex of degree 2. • More general separation procedure applies to any X ∈ D5 \ C5 that is not componentwise strictly positive. An even more general separation procedure th ...
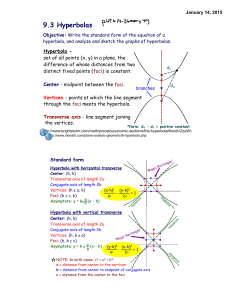
9.3 Hyperbolas
... Ex5: Classify each of the following. a) ellipse (AC = 20) a) 4x + 5y - 9x + 8y = 0 b) parabola (AC = 0) b) 2x - 5x + 7y - 8 = 0 c) circle (A = C) c) 7x + 7y - 9x + 8y - 16 = 0 d) hyperbola (AC = -20) ...
... Ex5: Classify each of the following. a) ellipse (AC = 20) a) 4x + 5y - 9x + 8y = 0 b) parabola (AC = 0) b) 2x - 5x + 7y - 8 = 0 c) circle (A = C) c) 7x + 7y - 9x + 8y - 16 = 0 d) hyperbola (AC = -20) ...
Celsius, Fahrenheit, Slopes, Lines
... Connect the concept of linearity with real-world contexts. ...
... Connect the concept of linearity with real-world contexts. ...
Lafayette Parish School System
... inputs in their domains, and interpret statements that use function notation in terms of a context. Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemb ...
... inputs in their domains, and interpret statements that use function notation in terms of a context. Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemb ...
Students will For example, interpret P(1+r)n as the product of P
... Summary: This course builds on the foundation established in Algebra II. Major concepts include: polynomial functions, functions, exponents & logarithms, trigonometric functions, equations & applications, triangle trigonometry, trigonometric. The use of graphing calculators is an integral part of th ...
... Summary: This course builds on the foundation established in Algebra II. Major concepts include: polynomial functions, functions, exponents & logarithms, trigonometric functions, equations & applications, triangle trigonometry, trigonometric. The use of graphing calculators is an integral part of th ...
DIFFERENTIAL GEOMETRY HW 3 32. Determine the dihedral
... (d): Show that the Seifert-Weber space is a manifold at the vertex. Proof. To do so, we must show that a neighborhood of the vertex is a ball. At each vertex on the dodecahedron, draw oriented edges connecting the edges that meet at that vertex, labeled appropriately. In so doing, we end up with 20 ...
... (d): Show that the Seifert-Weber space is a manifold at the vertex. Proof. To do so, we must show that a neighborhood of the vertex is a ball. At each vertex on the dodecahedron, draw oriented edges connecting the edges that meet at that vertex, labeled appropriately. In so doing, we end up with 20 ...
Mathematics Department GRADE 8/Algebra I/451
... Use units as a way to understand problems and to guide the solution of multi-‐step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs ...
... Use units as a way to understand problems and to guide the solution of multi-‐step problems; choose and interpret units consistently in formulas; choose and interpret the scale and the origin in graphs ...