hyperbolic pairs and basis
... seen as the standard equation of a hyperbola. If we think of a quadratic form as generalizing norms – that is length, then we are observing that on a hyperbolic line length is not Euclidean, in fact, as the usual Euclidean length of (x, y), x2 + y 2 , gets large, the associated hyperbolic length get ...
... seen as the standard equation of a hyperbola. If we think of a quadratic form as generalizing norms – that is length, then we are observing that on a hyperbolic line length is not Euclidean, in fact, as the usual Euclidean length of (x, y), x2 + y 2 , gets large, the associated hyperbolic length get ...
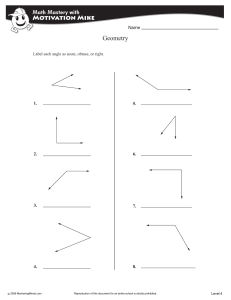
Geometry - 4thGrade
... 5. Lines E and F are intersecting lines, but they are not perpendicular. ...
... 5. Lines E and F are intersecting lines, but they are not perpendicular. ...
The regular polyhedra
... As far as showing that the regular solids can be constructed is concerned, the proof above is somewhat limited in relevance. It says no more and no less than that a single vertex of each of the regular polyhedra can be constructed. But constructing a vertex is not the same as constructing the whole ...
... As far as showing that the regular solids can be constructed is concerned, the proof above is somewhat limited in relevance. It says no more and no less than that a single vertex of each of the regular polyhedra can be constructed. But constructing a vertex is not the same as constructing the whole ...
Sample pages 1 PDF
... Theorem 2.5 (The rational root theorem). If x = p/q is a rational zero of a polynomial P(x) = an xn + · · · + a0 with integer coefficients and (p, q) = 1, then p | a0 and q | an . Theorem 2.6 (The fundamental theorem of algebra). Every nonconstant polynomial with coefficients in C has a complex root ...
... Theorem 2.5 (The rational root theorem). If x = p/q is a rational zero of a polynomial P(x) = an xn + · · · + a0 with integer coefficients and (p, q) = 1, then p | a0 and q | an . Theorem 2.6 (The fundamental theorem of algebra). Every nonconstant polynomial with coefficients in C has a complex root ...
DuarteFrancisSeville30apr13
... Thus, the user continues to brace rhombi and test for distortions. If a shift about every ribbon is a rigid rotation, then we have a rigidly braced carpet. Now consider the inverse problem. Is it perhaps possible to remove some of the bracings without affecting the rigidity? Bracing and unbracing rh ...
... Thus, the user continues to brace rhombi and test for distortions. If a shift about every ribbon is a rigid rotation, then we have a rigidly braced carpet. Now consider the inverse problem. Is it perhaps possible to remove some of the bracings without affecting the rigidity? Bracing and unbracing rh ...
Set 4 Special Congruent Triangles
... 1. Isosceles triangles have how many equal sides? __________________ 2. Isosceles triangles have two equal angles. Where are these equal angles located? 3. If -ABC is an isosceles triangle, then which sides of the triangle are congruent? Points D and E are on AC such that AD % DB and BE % EC . 4. Ho ...
... 1. Isosceles triangles have how many equal sides? __________________ 2. Isosceles triangles have two equal angles. Where are these equal angles located? 3. If -ABC is an isosceles triangle, then which sides of the triangle are congruent? Points D and E are on AC such that AD % DB and BE % EC . 4. Ho ...
Olymon Volume 1 - Department of Mathematics, University of Toronto
... for 0 ≤ x ≤ 1. For this least value of p, what is the smallest value of q for which the inequality is satisfied for 0 ≤ x ≤ 1? 42. G is a connected graph; that is, it consists of a number of vertices, some pairs of which are joined by edges, and, for any two vertices, one can travel from one to ano ...
... for 0 ≤ x ≤ 1. For this least value of p, what is the smallest value of q for which the inequality is satisfied for 0 ≤ x ≤ 1? 42. G is a connected graph; that is, it consists of a number of vertices, some pairs of which are joined by edges, and, for any two vertices, one can travel from one to ano ...
the isoperimetric problem on some singular surfaces
... show that minimizers are spherical and not simply constant mean curvature. Hugh Howards, Michael Hutchings, and Frank Morgan [9] provide a survey of leastperimeter enclosures. Some higher dimensional ambients with conical singularities are treated in [15] and [3]. 2. Existence and regularity We cons ...
... show that minimizers are spherical and not simply constant mean curvature. Hugh Howards, Michael Hutchings, and Frank Morgan [9] provide a survey of leastperimeter enclosures. Some higher dimensional ambients with conical singularities are treated in [15] and [3]. 2. Existence and regularity We cons ...
on three classes of regular toroids
... class T1 , it can easily be seen that a toroid with less than seven vertices does not exist. The model of the toroid, denoted by C0 , which is constructed on the basis of the data published by professor Ákos Császár at Budapest University who is a member of the Hungarian Academy of Sciences [2], app ...
... class T1 , it can easily be seen that a toroid with less than seven vertices does not exist. The model of the toroid, denoted by C0 , which is constructed on the basis of the data published by professor Ákos Császár at Budapest University who is a member of the Hungarian Academy of Sciences [2], app ...
Dissection of a triangle into similar triangles
... The construction from figure 1 shows that every triangle T has a dissection into any even, greater than or equal to 4 number of tiles. Thus, by dividing one tile into 4 pieces we obtain a dissection into any odd, greater than or equal to 7 number of tiles. The dissection from figure 1 is mostly perf ...
... The construction from figure 1 shows that every triangle T has a dissection into any even, greater than or equal to 4 number of tiles. Thus, by dividing one tile into 4 pieces we obtain a dissection into any odd, greater than or equal to 7 number of tiles. The dissection from figure 1 is mostly perf ...
Topic 3 Space, Shape and Orientation
... Note: • The sum of the interior angles of a polygon of n sides is 180 ° × (n – 2) • The size of an interior angle of a regular polygon of n sides is ...
... Note: • The sum of the interior angles of a polygon of n sides is 180 ° × (n – 2) • The size of an interior angle of a regular polygon of n sides is ...
Acute Triangulation of Rectangles
... degrees of freedom being 0. This is the last formed triangle in the triangulation. If an initial sequence of freedom degree is set, we can develop it into a sequence in which all numbers are natural numbers, and this sequence of operation is permissible. It can be proved that any triangulation can b ...
... degrees of freedom being 0. This is the last formed triangle in the triangulation. If an initial sequence of freedom degree is set, we can develop it into a sequence in which all numbers are natural numbers, and this sequence of operation is permissible. It can be proved that any triangulation can b ...
Warm Up - BFHS
... this square is multiplied by x, the resulting square has an area of 900 square centimeters. Find the value of x. ...
... this square is multiplied by x, the resulting square has an area of 900 square centimeters. Find the value of x. ...
MATH 120-04 - CSUSB Math Department
... , because the fundamental sine function is odd, so its graph is just the reflection of in the -axis.) It is important to remember that stretch and compression are in relation to the vertical axis, which is different from dilation about a point. Thus, the point where a horizontal line intersects is t ...
... , because the fundamental sine function is odd, so its graph is just the reflection of in the -axis.) It is important to remember that stretch and compression are in relation to the vertical axis, which is different from dilation about a point. Thus, the point where a horizontal line intersects is t ...
Theta Year 7 Scheme of Work KS3 Maths Progress Theta 3
... simplify and manipulate algebraic expressions to maintain equivalence: collecting like terms simplify and manipulate algebraic expressions to maintain equivalence: taking out common factors use algebraic methods to solve linear equations in one variable (including all forms that require rearrangemen ...
... simplify and manipulate algebraic expressions to maintain equivalence: collecting like terms simplify and manipulate algebraic expressions to maintain equivalence: taking out common factors use algebraic methods to solve linear equations in one variable (including all forms that require rearrangemen ...
Techniques of combinatorial optimization
... The following result follows from an immediate application of the Theorem of Alternatives and Farkas Lemma 1.3.2. Lemma 1.4.1. (i) (P) is unfeasible if and only if there exists u ∈ Rm such that u ≥ 0, uT A = 0T and uT b < 0. (ii) (D) is unfeasible if and only if there exists u ∈ Rn such that Au ≥ 0, ...
... The following result follows from an immediate application of the Theorem of Alternatives and Farkas Lemma 1.3.2. Lemma 1.4.1. (i) (P) is unfeasible if and only if there exists u ∈ Rm such that u ≥ 0, uT A = 0T and uT b < 0. (ii) (D) is unfeasible if and only if there exists u ∈ Rn such that Au ≥ 0, ...