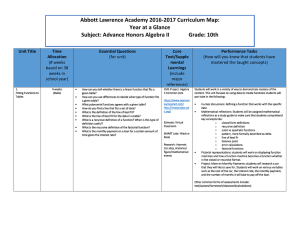
Abbott Lawrence Academy 2016-2017 Curriculum Map: Year at a
... Project: Factoring a Sequence of Polynomials: students will demonstrate the relationship between cyclotomic polynomials and integers by building tables in the factors of xn-1. ...
... Project: Factoring a Sequence of Polynomials: students will demonstrate the relationship between cyclotomic polynomials and integers by building tables in the factors of xn-1. ...
- Kennedy HS
... Bring compass, straightedge, and graph paper tomorrow. When 2 figures are congruent, they have the same size AND same shape. This means that the corresponding sides and the corresponding angles are congruent in congruent polygons. When 2 polygons are not congruent, they can be different sizes or dif ...
... Bring compass, straightedge, and graph paper tomorrow. When 2 figures are congruent, they have the same size AND same shape. This means that the corresponding sides and the corresponding angles are congruent in congruent polygons. When 2 polygons are not congruent, they can be different sizes or dif ...
TRIANGULATING POLYGONS WITHOUT LARGE ANGLES 1
... forces us to seek only an approximate solution. Steiner points also add another parameter to the quality of the output: the number of triangles in the triangulation, which we call the size of the triangulation. Size directly a ects computation times in nite element methods, or expense in measuring ...
... forces us to seek only an approximate solution. Steiner points also add another parameter to the quality of the output: the number of triangles in the triangulation, which we call the size of the triangulation. Size directly a ects computation times in nite element methods, or expense in measuring ...
Number Algebra Shape, space and measures Handling data G write
... show how 2 congruent scalene triangles put together can make an isos. triangle use a map and scale to measure and find distance plot a point given bearing (obtuse) and distance work out area of 4.6 by 5.2 rectangle and perimeter ...
... show how 2 congruent scalene triangles put together can make an isos. triangle use a map and scale to measure and find distance plot a point given bearing (obtuse) and distance work out area of 4.6 by 5.2 rectangle and perimeter ...
RELATIONS BETWEEN CUMULANTS IN NONCOMMUTATIVE PROBABILITY
... Fourier analysis is the tool of choice for most problems in classical probability, cumulants are an indispensable ingredient for many investigations in noncommutative probability. An intriguing aspect of noncommutative probability is the existence of several kinds of independence [Voi85, SW97, Mur01 ...
... Fourier analysis is the tool of choice for most problems in classical probability, cumulants are an indispensable ingredient for many investigations in noncommutative probability. An intriguing aspect of noncommutative probability is the existence of several kinds of independence [Voi85, SW97, Mur01 ...
File
... The amplitude of y = a sin x (or y = a cos x) is half the distance between the maximum and minimum values of the function. amplitude = |a| If |a| > 1, the amplitude stretches the graph vertically. If 0 < |a| > 1, the amplitude shrinks the graph vertically. If a < 0, the graph is reflected in the x- ...
... The amplitude of y = a sin x (or y = a cos x) is half the distance between the maximum and minimum values of the function. amplitude = |a| If |a| > 1, the amplitude stretches the graph vertically. If 0 < |a| > 1, the amplitude shrinks the graph vertically. If a < 0, the graph is reflected in the x- ...
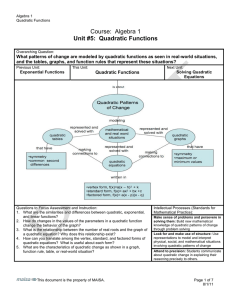
Course: Algebra 1 Unit #5: Quadratic Functions
... 5. Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the functionh(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the funct ...
... 5. Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the functionh(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the funct ...
spectra of large random trees
... The recent availability of large amounts of data has led to an explosion in the number of models used to model real-world networks, and dynamically grown models such as various preferential attachment schemes have attracted significant interest from the computer science and mathematical physics commu ...
... The recent availability of large amounts of data has led to an explosion in the number of models used to model real-world networks, and dynamically grown models such as various preferential attachment schemes have attracted significant interest from the computer science and mathematical physics commu ...
Reasoning and Proof in a Spatial Geometry
... Question 2. Produce them with specific materials. Question 3. Prove that the previously established list is valid and complete. 2.2. Mathematical analysis of the problem First, let’s look at the definition. There are several possibilities, which from the start raises the question of their equivalenc ...
... Question 2. Produce them with specific materials. Question 3. Prove that the previously established list is valid and complete. 2.2. Mathematical analysis of the problem First, let’s look at the definition. There are several possibilities, which from the start raises the question of their equivalenc ...
Mitri Kitti Axioms for Centrality Scoring with Principal Eigenvectors
... corresponding graph in which there is an edge between nodes i and j if aij > 0. Without loss of generality we may assume that the weight of the edge is aij . Let G(A) denote the directed graph corresponding to A. It will be assumed that A is irreducible; nodes that cannot be connected to each other ...
... corresponding graph in which there is an edge between nodes i and j if aij > 0. Without loss of generality we may assume that the weight of the edge is aij . Let G(A) denote the directed graph corresponding to A. It will be assumed that A is irreducible; nodes that cannot be connected to each other ...
ppt - Chair of Computational Biology
... corresponding row of the initial matrix by -1. If the exchange flux is unconstrained move the entire row to a temporary matrix T(E). This completes the first tableau T(0). T(0) and T(E) for the example reaction system are shown on the previous slide. Each element of these matrices will be designat ...
... corresponding row of the initial matrix by -1. If the exchange flux is unconstrained move the entire row to a temporary matrix T(E). This completes the first tableau T(0). T(0) and T(E) for the example reaction system are shown on the previous slide. Each element of these matrices will be designat ...
On the approximability of the maximum feasible subsystem
... 1.2 Our results In this paper, we consider only max- 6. Due to lack of space, we only present sketches for imum feasible subsystems where the constraint matrix most of the proofs. The final version of the paper will is a 0/1 matrix with non-negative solutions. Under this contain complete proofs. res ...
... 1.2 Our results In this paper, we consider only max- 6. Due to lack of space, we only present sketches for imum feasible subsystems where the constraint matrix most of the proofs. The final version of the paper will is a 0/1 matrix with non-negative solutions. Under this contain complete proofs. res ...
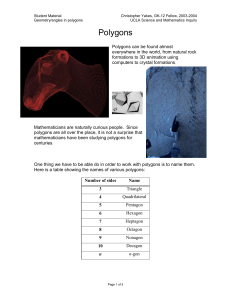
Polygons_worksheet3 - Penns Valley Math Resources
... EXERCISE 3: What is the sum of the interior angles of a 13-gon? EXERCISE 4: Can the sum of the interior angles of a polygon be 450º? EXERCISE 5: What is the measure of the interior angle of a regular ...
... EXERCISE 3: What is the sum of the interior angles of a 13-gon? EXERCISE 4: Can the sum of the interior angles of a polygon be 450º? EXERCISE 5: What is the measure of the interior angle of a regular ...
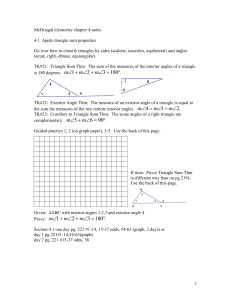
McDougal Geometry chapter 4 notes
... TK#33: Corollary to Base Angles Thm: If a triangle is equilateral, then it is equiangular. TK#34: Corollary to Converse of Base Angles Thm: If a triangle is equiangular, then it is equilateral. Prove the Base Angles Thm. (Use the back of this page.) Guided practice 1-5. (Use the back of this page.) ...
... TK#33: Corollary to Base Angles Thm: If a triangle is equilateral, then it is equiangular. TK#34: Corollary to Converse of Base Angles Thm: If a triangle is equiangular, then it is equilateral. Prove the Base Angles Thm. (Use the back of this page.) Guided practice 1-5. (Use the back of this page.) ...
Coordinate geometry: working with slopes
... c. What is special about triangle ABC? Justify your answer using slopes. 2. You can calculate the midpoint of a line segment by thinking of the two endpoints as a data set and finding their average. The midpoint’s x-coordinate is the average of the x-coordinates of the endpoints, and the midpoint’s ...
... c. What is special about triangle ABC? Justify your answer using slopes. 2. You can calculate the midpoint of a line segment by thinking of the two endpoints as a data set and finding their average. The midpoint’s x-coordinate is the average of the x-coordinates of the endpoints, and the midpoint’s ...
Ways to find slope
... d. How many right angles does this quadrilateral have? Tell how you know. 5. Consider quadrilateral WXYZ with vertices W(–2, 3), X(–1, 8), Y(9, 6), and Z(8, 1). a. Is this quadrilateral a parallelogram? Justify your answer using slopes. b. Is this quadrilateral a trapezoid? Justify your answer using ...
... d. How many right angles does this quadrilateral have? Tell how you know. 5. Consider quadrilateral WXYZ with vertices W(–2, 3), X(–1, 8), Y(9, 6), and Z(8, 1). a. Is this quadrilateral a parallelogram? Justify your answer using slopes. b. Is this quadrilateral a trapezoid? Justify your answer using ...
Answer - Imagine School at Lakewood Ranch
... Find the degrees for each part. Round to the nearest whole degree. ...
... Find the degrees for each part. Round to the nearest whole degree. ...
computational
... Distance function not differentiable on the medial axis Still can define a generalized concept of gradient ...
... Distance function not differentiable on the medial axis Still can define a generalized concept of gradient ...
SAT Subject Tests - collegereadiness
... these four intervals, there is a value k in that interval such that f (k) = 2. This shows that there are at least four such values of k, and the fact that x 4 − 3x 3 − 9x 2 + 4 is a polynomial of degree 4 means that there can be at most four such values of k. Therefore, there are four values of ...
... these four intervals, there is a value k in that interval such that f (k) = 2. This shows that there are at least four such values of k, and the fact that x 4 − 3x 3 − 9x 2 + 4 is a polynomial of degree 4 means that there can be at most four such values of k. Therefore, there are four values of ...
Nonoverlap of the Star Unfolding
... To create such an overlap, we must start with a vertex in the polyhedron with negative curvature, then cut in such a way that one image of the vertex will retain at least 2π of the surface material. Convex polyhedra clearly avoid 1-local overlaps, since they contain no vertices with negative curvatu ...
... To create such an overlap, we must start with a vertex in the polyhedron with negative curvature, then cut in such a way that one image of the vertex will retain at least 2π of the surface material. Convex polyhedra clearly avoid 1-local overlaps, since they contain no vertices with negative curvatu ...