Download File

Gettin’ Triggy wit it
http://www.youtube.com/watch?v=t2uPYYL
H4Zo
An angle is formed by joining the endpoints
of two half-lines called rays.
The side you measure to is called the terminal side.
Angles measured counterclockwise are given a
positive sign and angles measured clockwise are
given a negative sign.
Negative Angle
This is a
clockwise
rotation.
Positive Angle
This is a
counterclockwise
rotation.
Initial Side
The side you measure from is called the initial side.
It’s Greek To Me!
It is customary to use small letters in the Greek alphabet
to symbolize angle measurement.

alpha

theta

beta

gamma
We can use a coordinate system with angles by putting
the initial side along the positive x-axis with the vertex
at the origin.
Quadrant
Quadrant I
II
angle
angle
 positive
 negative
Initial Side
Quadrant
If the terminal side is along
IV
an axis it is called a
angle
quadrantal angle.
We say the angle lies in whatever quadrant the terminal
side lies in.
We will be using two different units of measure
when talking about angles: Degrees and Radians
 = 360°
If we start with the initial side and go all of
the way around in a counterclockwise
direction we have 360 degrees
 = 90°
If we went 1/4 of the way in
a clockwise direction the
angle would measure -90°
 = - 90°
You are probably already
familiar with a right angle
that measures 1/4 of the
way around or 90°
Let’s talk about degrees first. You are probably already
somewhat familiar with degrees.
What is the measure of this angle?
You could measure in the positive
 = - 360° + 45°
direction and go around another rotation
which would be another 360°
 = - 315°
 = 45°
You could measure in the positive
direction
 = 360° + 45° = 405°
You could measure in the negative
direction
There are many ways to express the given angle.
Whichever way you express it, it is still a Quadrant I
angle since the terminal side is in Quadrant I.
If the angle is not exactly to the next degree it can be
expressed as a decimal (most common in math) or in
degrees, minutes and seconds (common in surveying
and some navigation).
1 degree = 60 minutes
1 minute = 60 seconds
 = 25°48‘29"
degrees
seconds
minutes
To convert to decimal form use conversion fractions.
These are fractions where the numerator = denominator
but two different units. Put unit on top you want to
convert to and put unit on bottom you want to get rid of.
Let's convert the
seconds to
minutes
30"  1'
60"
= 0.5'
1 degree = 60 minutes
1 minute = 60 seconds
 = 25°48'30" = 25°48.5' = 25.808°
Now let's use another conversion fraction to get rid of
minutes.
48.5'  1
60'
= .808°
Another way to measure angles is using what is called
radians.
Given a circle of radius r with the vertex of an angle as the
center of the circle, if the arc length formed by intercepting
the circle with the sides of the angle is the same length as
the radius r, the angle measures one radian.
arc length is
also r
r
r
r
initial side
radius of circle is r
This angle measures
1 radian
Arc length s of a circle is found with the following formula:
IMPORTANT: ANGLE
MEASURE MUST BE IN
RADIANS TO USE FORMULA!
s = r
arc length
radius
measure of angle
Find the arc length if we have a circle with a radius of 3
meters and central angle of 0.52 radian.
arc length to find is in black
 = 0.52
3
s = r30.52
= 1.56 m
What if we have the measure of the angle in degrees? We
can't use the formula until we convert to radians, but how?
We need a conversion from degrees to radians. We
could use a conversion fraction if we knew how many
degrees equaled how many radians.
Let's start with
the arc length
formula
cancel the r's
s = r
2r = r
2 = 
2  radians = 360°
If we look at one revolution
around the circle, the arc
length would be the
circumference. Recall that
circumference of a circle is
2r
This tells us that the
radian measure all the
way around is 2. All the
way around in degrees is
360°.
2  radians = 360°
 radians = 180°
Convert 30° to radians using a conversion fraction.
30°  2 radians
360
=

6
The fraction can be
reduced by 2. This
would be a simpler
conversion fraction.
180°
radians  0.52
Can leave with  or use  button on
your calculator for decimal.
Convert /3 radians to degrees using a conversion fraction.

180
radians 
3
 radians
= 60°
Area of a Sector of a Circle

r
The formula for the area of a
sector of a circle (shown in
red here) is derived in your
textbook. It is:
Again  must be in RADIANS
so if it is in degrees you must
convert to radians to use the
formula.
1 2
A r 
2
Find the area of the sector if the radius is 3 feet and  = 50°
50 
 radians
180
= 0.873 radians
1 2
A   3 0.873
2
 3.93 sq ft
A Sense of Angle Sizes

45 
4

30 
6

90 
2
See if you can guess
the size of these
angles first in degrees
and then in radians.
2
120 
3
5
150
6

60 
3
180  
3
135
4
You will be working so much with these angles, you
should know them in both degrees and radians.
Angles, Arc
length,
Conversions
Angle measured in standard position.
Initial side is the positive x – axis which is fixed.
Terminal side is the ray in quadrant II, which is free
to rotate about the origin. Counterclockwise rotation
is positive, clockwise rotation is negative.
Coterminal Angles: Angles that have the same terminal side.
60°, 420°, and –300° are all coterminal.
Degrees to radians: Multiply angle by   . 60       radians
180
3
180
Radians to degrees: Multiply angle by
 180 

. 4    45

180
Note: 1 revolution = 360° = 2π radians.
Arc length = central angle x radius, or s  r.
Note: The central angle must be in radian measure.
6.2 TRIGONOMETRY
Remember SOHCAHTOA
• Sine is Opposite
divided by
Hypotenuse
• Cosine is Adjacent
divided by
Hypotenuse
• Tangent is Opposite
divided by Adjacent
• SOHCAHTOA!!!!!!
• http://www.youtube.com/watch?v=4iCgjKvc7A&feature=related
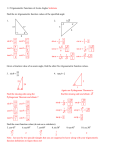
Right Triangle
Trig Definitions
B
c
a
C
•
•
•
•
•
•
b
A
sin(A) = sine of A = opposite / hypotenuse = a/c
cos(A) = cosine of A = adjacent / hypotenuse = b/c
tan(A) = tangent of A = opposite / adjacent = a/b
csc(A) = cosecant of A = hypotenuse / opposite = c/a
sec(A) = secant of A = hypotenuse / adjacent = c/b
cot(A) = cotangent of A = adjacent / opposite = b/a
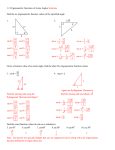
Special Right Triangles
30°
45°
2
2
3
1
3
cos(30 ) 
2
1
sin( 30  ) 
2
3
tan( 30  ) 
3

1
60°
1
2
3
sin( 60  ) 
2
tan( 60  )  3
cos(60  ) 
1
2
2
2
sin( 45  ) 
2
tan( 45  )  1
cos( 45  ) 
45°
6.2 Assignment (day 1)
pp. 417-419 (1-23 odd, 27, 29)
21, 23
Basic Trigonometric Identities
Quotient identities: tan( A) 
Even/Odd identities:
sin( A)
cos( A)
cos( A)
sin( A)
cot( A) 
cos(  A)  cos( A)
sec(  A)  sec( A)
sin(  A)   sin( A)
csc(  A)   csc( A)
tan(  A)   tan( A)
cot(  A)   cot( A)
Even functions
Odd functions
Odd functions
Reciprocal Identities:
1
csc( A) 
sin( A)
1
sin( A) 
csc( A)
1
sec( A) 
cos( A)
1
cos( A) 
sec( A)
1
cot( A) 
tan( A)
1
tan( A) 
cot( A)
Pythagorean Identities:
sin 2 ( A)  cos 2 ( A)  1
tan 2 ( A)  1  sec 2 ( A)
1  cot 2 ( A)  csc 2 ( A)
All Students Take Calculus.
Quad I
Quad II
Quad III
cos(A)<0
sin(A)>0
tan(A)<0
sec(A)<0
csc(A)>0
cot(A)<0
cos(A)>0
sin(A)>0
tan(A)>0
sec(A)>0
csc(A)>0
cot(A)>0
cos(A)<0
sin(A)<0
tan(A)>0
sec(A)<0
csc(A)<0
cot(A)>0
cos(A)>0
sin(A)<0
tan(A)<0
sec(A)>0
csc(A)<0
cot(A)<0
Quad IV
• http://www.youtube.com/watch?v=Ah9NxA
GzlDc&feature=related
6.3 Trigonometric Functions of Real
Numbers
Exact Values Using Points on the
Circle
• Example. Let t be a real number and P =
the point on the unit circle that corresponds
to t.
Problem: Find the values of sin t, cos t, tan t, csc
t, sec t and cot t
Answer:
Exact Values for Quadrantal Angles
• Example. Find the values of the
trigonometric functions of µ
Problem: µ = 0 = 0±
Answer:
Exact Values for Quadrantal Angles
• Example. Find the values of the
trigonometric functions of µ
Problem: µ =
Answer:
= 90±
Exact Values for Quadrantal Angles
• Example. Find the values of the
trigonometric functions of µ
Problem: µ = ¼ = 180±
Answer:
Circles of Radius r
• Example.
Problem: Find the exact values of each of the
trigonometric functions of an angle θ if ({12,
5}) is a point on its terminal side.
Answer:
Even-Odd Properties
• Theorem. [Even-Odd Properties]
sin(θ) = sin(θ)
cos(θ) = cos(θ)
tan(θ) = tan(θ)
csc(θ) = csc(θ)
sec(θ) = sec(θ)
cot(θ) = cot(θ)
• Cosine and secant are even functions
• The other functions are odd functions
The Sine Function
The sine of a real number t is the y–coordinate
(height) of the point P in the following
diagram, where |t| is the length of the arc.
1 y
sin t
–1
P
|t|
1 unit 1
–1
x
sin t    sint 
An odd function.
Properties of Sine and Cosine Functions
The graphs of y = sin x and y = cos x have similar properties:
1. The domain is the set of real numbers.
2. The range is the set of y values such that  1  y  1.
3. The maximum value is 1 and the minimum value is –1.
4. The graph is a smooth curve.
5. Each function cycles through all the values of the range
over an x-interval of 2 .
6. The cycle repeats itself indefinitely in both directions of the
x-axis.
The Sine Function
1.5
Highlight those
sections of the circle
where sin(t) >0
1
sin(0)  0
0.5 > 0
sin(t)
0
-1.5
-1
-0.5
0.5
-0.5
-1
-1.5
1
1.5
 
sin    1
2
sin    0
 3
sin 
 2

  1

The Sine Function


2
2
3
2
Graph of the Sine Function
To sketch the graph of y = sin x first locate the key points.
These are the maximum points, the minimum points, and the
intercepts.

3
x
0

2
2
sin x
0
2
1
0
-1
0
Then, connect the points on the graph with a smooth curve
that extends in both directions beyond the five points. A
single cycle is called a period.
y = sin x
y
3

2



1

2
2
1

3
2
2
5
2
x
The Cosine Function
The cosine of a real number t is the x–
coordinate (length) of the point P in the
following diagram, where |t| is the length of
the arc.
y
1
–1 1 unit
P
|t|
cos t 1
–1
x
cos t   cost 
An even function.
The Cosine Function
1.5
Highlight those
sections where
cos(t) > 0
1
cos(0)  1
0.5
cos(t)0.5
>0
0
-1.5
-1
-0.5
-0.5
-1
-1.5
1
1.5
 
cos    0
2
cos    1
 3
cos 
 2

0

The Cosine Function


2
2
3
2
Graph of the Cosine Function
To sketch the graph of y = cos x first locate the key points.
These are the maximum points, the minimum points, and the
intercepts.

3
x
0

2
2
cos x
1
2
0
-1
0
1
Then, connect the points on the graph with a smooth curve
that extends in both directions beyond the five points. A
single cycle is called a period.
y = cos x
y
3

2



1

2
2
1

3
2
2
5
2
x
Graphing the Tangent Function
• Periodicity: Only need to graph on interval
[0, ¼]
• Plot points and graph
Graphing the Cotangent Function
• Periodicity: Only need to graph on interval
[0, ¼]
Graphing the Cosecant and Secant
Functions
• Use reciprocal identities
• Graph of y = csc x
Graphing the Cosecant and Secant
Functions
• Use reciprocal identities
• Graph of y = sec x
6.4 Values of the Trigonometric
Functions
6.4 Reference Angles
•
A reference angle for an angle , written  , is
the positive acute angle made by the terminal
side of angle  and the x-axis.
Example Find the reference angle for each angle.
(a) 218º
(b) 5
6
Solution
5 
(a)   = 218º – 180º = 38º (b)     

6
6
6.4 Special Angles as Reference Angles
Example Find the values of the trigonometric
functions for 210º.
Solution
The reference angle for 210º is
210º – 180º = 30º.
Choose point P on the terminal
side so that the distance from
the origin to P is 2. A 30º - 60º
right triangle is formed.
1
3
3


sin 210  
cos 210  
tan 210 
2
2
3
2 3



csc 210  2 sec 210  
cot 210  3
3

6.4 Finding Trigonometric Function
Values Using Reference Angles
Example Find the exact value of each expression.
(a) cos(–240º)
(b) tan 675º
Solution
(a) –240º is coterminal with 120º.
The reference angle is
180º – 120º = 60º. Since –240º
lies in quadrant II, the
cos(–240º) is negative.
1
cos( 240 )   cos 60  
2
Similarly,
tan 675º = tan 315º
= –tan 45º = –1.

•

Quad II
Reference AnglesQuad I
θ’ = 180° – θ
θ’ = θ
θ’ = π – θ
θ’ = θ – 180°
θ’ = θ – π
Quad III
θ’ = 360° – θ
θ’ = 2π – θ
Quad IV
6.4 Finding Trigonometric Function
Values with a Calculator
Example Approximate the value of each expression.
(a) cos 49º 12
(b) csc 197.977º
Solution Set the calculator in degree mode.
6.4 Finding Angle Measure
Example Using Inverse Trigonometric Functions to Find
Angles
(a) Use a calculator to find an angle  in degrees that satisfies
sin   .9677091705.
(b) Use a calculator to find an angle  in radians that satisfies
tan   .25.
Solution
(a) With the calculator in degree mode,
we find that an angle having a sine
value of .9677091705 is 75.4º. Write
this as sin-1 .9677091705  75.4º.
(b) With the calculator in radian mode,
we find tan-1 .25  .2449786631.
6.4 Finding Angle Measure
Example Find all values of , if  is in the interval
[0º, 360º) and cos   22 .
Solution Since cosine is negative,  must lie in
either quadrant II or III. Since cos  22 , cos 1 22  45.
So the reference angle   = 45º.
The quadrant II angle  = 180º – 45º = 135º, and the
quadrant III angle  = 180º + 45º = 225º.
6.4 Review Answers
6.4 Review
6.5 Graphs of
Trigonometric Functions
6.5 Trigonometric Graphs
Objective: We will re-define the basic trig.
functions and their graphs and go more in
depth with vertical stretches, horizontal
stretches, periods, amplitudes, and shifts up
and down.
Sine graphs
y = sin(x)
y = 3sin(x)
y = sin(x) + 3
y = sin(3x)
y = sin(x – 3)
y = sin(x/3)
y = 3sin(3x-9)+3
y = sin(x)
Graphs of cosine
y = cos(x)
y = cos(x) + 3
y = 3cos(x)
y = cos(3x)
y = cos(x – 3)
y = cos(x/3)
y = 3cos(3x – 9) + 3
y = cos(x)
6.5 (Sine & Cosine)
Review: y = sin x
y = cos x
a varies height/
vertical stretch of graph
amplitude = |a|
a varies height/ 1
vertical stretch of graph
amplitude = |a|
Π
Π
2Π
-1
y = asin(bx+c) +d
*y = 3 sin x
*y = ½ sin x
y = acos(bx+c) +d
*y = 2 cos x
*y = -2cos x
2Π
The amplitude of y = a sin x (or y = a cos x) is half the distance
between the maximum and minimum values of the function.
amplitude = |a|
If |a| > 1, the amplitude stretches the graph vertically.
If 0 < |a| > 1, the amplitude shrinks the graph vertically.
If a < 0, the graph is reflected in the x-axis.
y
4
y = 2sin x

2
y=
1
2

3
2
2
x
sin x
y = – 4 sin x
reflection of y = 4 sin x
4
y = sin x
y = 4 sin x
Example: Sketch the graph of y = 3 cos x on the interval [–, 4].
Partition the interval [0, 2] into four equal parts. Find the five key
points; graph one cycle; then repeat the cycle over the interval.
x
y = 3 cos x
y

(0, 3)
2
1

0
3
0

-3
x-int
min
2
max
3
2
0
2
3
x-int
max
(2 , 3)

1 
( , 0)
2
2
3
( , –3)
2
( 3 , 0)
2
3
4 x
Use basic trigonometric identities to graph y = f (–x)
Example 1: Sketch the graph of y = sin (–x).
The graph of y = sin (–x) is the graph of y = sin x reflected in
the x-axis.
y = sin (–x)
y
Use the identity
sin (–x) = – sin x
y = sin x
x

2
Example 2: Sketch the graph of y = cos (–x).
The graph of y = cos (–x) is identical to the graph of y = cos x.
y
Use the identity
x
cos (–x) = cos x

2
y = cos (–x)
The period of a function is the x interval needed for the
function to complete one cycle.
For b  0, the period of y = a sin bx is 2 .
b
For b  0, the period of y = a cos bx is also 2 .
b
If 0 < b < 1, the graph of the function is stretched horizontally.
y
y  sin 2 x
period: 2
period: 
y  sin x x


2
If b > 1, the graph of the function is shrunk horizontally.
y
y  cos x
1
y  cos x
period: 2
2 
2
3
4

x
period: 4
y=asin(bx+c) +d
y=acos(bx+c) +d
b
varies width/horizontal stretch
Period = 2 Π
b
y = 3 sin 2x
amp: |a| =
per: 2 Π =
b
** this means there is 1 sine wave on the
interval [0, Π] **
Sketch the graph.
1
2
Y = 2sin x
amp: |a| =
per: 2 Π =
b
Graph:
Example: Sketch the graph of y = 2 sin (–3x).
Rewrite the function in the form y = a sin bx with b > 0
y = 2 sin (–3x) = –2 sin 3x
Use the identity sin (– x) = – sin x:
2  2
period:
amplitude: |a| = |–2| = 2
=
3
b
Calculate the five key points.
x
0
y = –2 sin 3x
0
y

2


6
3
2
2
3
–2
0
2
0
(  , 2)


6
3
6
(0, 0)
2

(  ,-2)
6
2

2
3
2
(  , 0) 2
3
( , 0)
3
5
6

x
d
• y= 2sinx + 3
shifts up & down
y = cosx - 2
y = asin(bx+c); phase shift = -c/b;
0≤bx+c≤2Π
• y = 3 sin(2x+Π)
2
amp: |a| =
per: 2 Π =
b
p.s. =
0 ≤ 2x+Π ≤ 2Π
2
Express in the form:
y = asin(bx+c) for a,b,c,> 0
5
a=
b=
p.s. =
-4
-2
-5
2
4
Example
Determine the amplitude, period, and phase
shift of y = 2sin(3x-)
Solution:
Amplitude = |A| = 2
period = 2/B = 2/3
phase shift = -C/B = /3
Example cont.
• y = 2sin(3x- )
3
2
1
-6 -5 -4 -3 -2 -1
-1
-2
-3
1 2 3 4 5 6
a sin( bx  c)  d
Amplitude
Period:
2π/b
Phase Shift:
-c/b
Vertical
Shift
6.6 More Trig. Graphs
Objective: Students will look at more trig.
graphs, including the tangent and reciprocal
functions, and the variations on these
reciprocal functions and their graphs.
6.6
Variations on reciprocal functions:
Amplitude has no meaning (tan/cot)
“a” still varies vertical stretch
2

“b” still affects period tanθ, cot θ = | b | csc θ, sec θ = | b |
c

“c” still affects phase shift
b
“d” still varies vertical shifts
6.6
y = tan x
-2Π
y = a tan(bx+c) +d
amplitude:
period:
phase shift:
-Π
Π
2Π
Successive vertical asymptotes:


2
<bx+c<

2
6.6
y=
1
2
tan (x +
period:
p.s.

4
)
6.6
y = cot x
y = csc x
y = sec x
y = csc (2x + Π)
=
1
sin( 2 x  )
Recall: csc θ =
amp:
per:
p.s.
1
sin 
6.7 Applied Problems
Objective: Students will use trig. functions in
applying real-world application problems.
6.7
Ex: (#25 from assignment)
x ft.
500 ft.
60°
4 ft.
SOH-CAH-TOA
x
sin 60 = 500
x = 433 ft + 4 = 437
Ch. 6 Test Review