* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
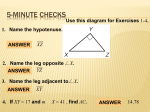
Download Exercises 4 1. The point is on the terminal side of an angle in
Survey
Document related concepts
Transcript
Exercises 4 1. The point is on the terminal side of an angle in standard position. Determine the exact values of the six trigonometric functions of the angle. (a) (8, 15) (b) (−4.10) (c) (3 12 , −7 34 ) 2. find the values of the six trigonometric functions of θ with the given constraint. (a) cos θ = (b) cos θ = 8 17 , tan θ < 0 − 45 , θ lie in the Quadrant III (c) csc θ = 4, θ < 0 (d) cot θ is undifined π 2 <θ< 3π 2 3. the terminal side of θ lies on the given line in the specified quadrant. Find the values of the six trigonometric functions of θ by finding a point on the line. (a) y = x 3 in Quadrant II (b) 4x + 3y = 0 in Quadrant IV 4. evaluate the sine, cosine, and tangent of the angle without using a calculator. (a) 300◦ (b) −406◦ (c) (d) 10π 3 −23π 4 5. find two solutions of the equation. Give your answers in degrees (0◦ ≤ θ < 360◦ ) and in radians (0 ≤ θ < 2π) (a) csc θ = √ 2 3 3 (b) sec θ = −2 √ (c) sin θ = − 3 2 6. To find the reference angle for an angle θ (given in degrees), find the integer n such that 0 ≤ 360◦ n−θ ≤ 360◦ The difference 360◦ n − θ is the reference angle. Determine whether the statement is true or false. Justify your answer. 7. The current I(in amperes) when 100 volts is applied to a circuit is given by I = 5e−2t sin t where t is the time (in seconds) after the voltage is applied. Approximate the current at t = 0.7 second after the voltage is applied. 1 8. The figure shows point P (x, y) on a unit circle and right triangle OAP (a) Find sin t and cos t using the unit circle definitions of sine and cosine. (b) What is the value of r? Explain. (c) Use the definitions of sine and cosine given in this section to find sin t and cos t Write your answers in terms of x and y (d) Based on your answers to parts (a) and (c), what can you conclude? 2