Fabian assignment
... 1, then O√ is at distance 2/2 from B, C, D, E and it is easy to see that O is also at distance 2/2 from A and F . Thus A, B, C, D, E, F lie on a sphere with center O. This was the same construction as in Proposition 2.7. The properties (d), (e), (f ) follow. Case 5 :(Exercise 44.5) Five equilateral ...
... 1, then O√ is at distance 2/2 from B, C, D, E and it is easy to see that O is also at distance 2/2 from A and F . Thus A, B, C, D, E, F lie on a sphere with center O. This was the same construction as in Proposition 2.7. The properties (d), (e), (f ) follow. Case 5 :(Exercise 44.5) Five equilateral ...
Connectivity, Devolution, and Lacunae in
... and are called geometric random graphs. In recent years these models have seen renewed interest spurred by applications in computational geometry, randomly deployed sensor networks, and cluster analysis; see the monograph by Penrose for a slew of references [6]. The digraph induced by a general mosa ...
... and are called geometric random graphs. In recent years these models have seen renewed interest spurred by applications in computational geometry, randomly deployed sensor networks, and cluster analysis; see the monograph by Penrose for a slew of references [6]. The digraph induced by a general mosa ...
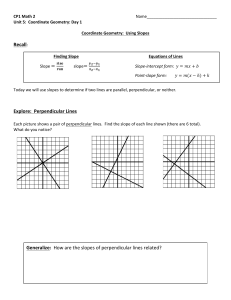
Math - broward.k12.fl.us
... 2) What is the ratio of videocassettes to the total number of items in the bag? There are 3 videocassettes, and 3 + 4 + 7 + 1 = 15 items total. The answer can be expressed as 3/15, 3 to 15, or 3:15. Proportions: ...
... 2) What is the ratio of videocassettes to the total number of items in the bag? There are 3 videocassettes, and 3 + 4 + 7 + 1 = 15 items total. The answer can be expressed as 3/15, 3 to 15, or 3:15. Proportions: ...
Polygons calculation of areas and overlap Delphi program “Polygon
... Reason is, that AS is a positive extension of AB and CS is a positive extension of CD. If S had been on AB and CD , then 0 < k < 1 and also 0 < m < 1. Negative values of k and m indicate, that S is positioned before (the head) of the vector so , AS would be a negative extension of AB (reversed direc ...
... Reason is, that AS is a positive extension of AB and CS is a positive extension of CD. If S had been on AB and CD , then 0 < k < 1 and also 0 < m < 1. Negative values of k and m indicate, that S is positioned before (the head) of the vector so , AS would be a negative extension of AB (reversed direc ...
RT -symmetric Laplace operators on star graphs: real spectrum and self-adjointness
... of the goals of the current article is to understand it in the case of the simplest merit graph with symmetries - the star graph. It can be considered as a building block to define differential operators on arbitrary metric graphs. To avoid discussing properties of the differential operator we limit ...
... of the goals of the current article is to understand it in the case of the simplest merit graph with symmetries - the star graph. It can be considered as a building block to define differential operators on arbitrary metric graphs. To avoid discussing properties of the differential operator we limit ...
Euler`s Polyhedral Formula - CSI Math Department
... Any plane graph can be made into a graph on a sphere by tying up the unbounded face (like a balloon). However one may need to make some modifications (which do not change the count v − e + f ) to make the graph geodesic on the sphere (keywords: k-connected for k = 1, 2, 3). Theorem If G is a connect ...
... Any plane graph can be made into a graph on a sphere by tying up the unbounded face (like a balloon). However one may need to make some modifications (which do not change the count v − e + f ) to make the graph geodesic on the sphere (keywords: k-connected for k = 1, 2, 3). Theorem If G is a connect ...
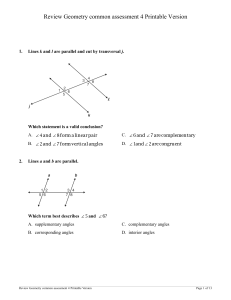
Curriculum Map - Georgia Standards
... Number and Quantity Strand: RN = The Real Number System, Q = Quantities, CN = Complex Number System, VM = Vector and Matrix Quantities Algebra Strand: SSE = Seeing Structure in Expressions, APR = Arithmetic with Polynomial and Rational Expressions, CED = Creating Equations, REI = Reasoning with Equa ...
... Number and Quantity Strand: RN = The Real Number System, Q = Quantities, CN = Complex Number System, VM = Vector and Matrix Quantities Algebra Strand: SSE = Seeing Structure in Expressions, APR = Arithmetic with Polynomial and Rational Expressions, CED = Creating Equations, REI = Reasoning with Equa ...
Acc-Algebra-I-Geometry-A-Curriculum-Map
... squares that can be factored as (x2 – y2) (x2 + y2). Write expressions in equivalent forms to solve problems. MGSE9-12.A.SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression. MGSE9-12.A.SSE.3a Factor any quadratic ...
... squares that can be factored as (x2 – y2) (x2 + y2). Write expressions in equivalent forms to solve problems. MGSE9-12.A.SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression. MGSE9-12.A.SSE.3a Factor any quadratic ...
Acc-Algebra-I-Geometry-A-Curriculum-Map
... squares that can be factored as (x2 – y2) (x2 + y2). Write expressions in equivalent forms to solve problems. MGSE9-12.A.SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression. MGSE9-12.A.SSE.3a Factor any quadratic ...
... squares that can be factored as (x2 – y2) (x2 + y2). Write expressions in equivalent forms to solve problems. MGSE9-12.A.SSE.3 Choose and produce an equivalent form of an expression to reveal and explain properties of the quantity represented by the expression. MGSE9-12.A.SSE.3a Factor any quadratic ...
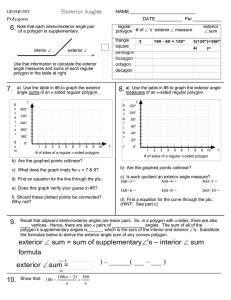
6. 8. exterior ∠ sum = sum of supplementary∠`s – interior ∠ sum
... Recall that adjacent interior/exterior angles are linear pairs. So, in a polygon with n-sides, there are also ____ vertices. Hence, there are also n pairs of _____________ angles. The sum of all of the polygon’s supplementary angles is______, which is the sum of the interior and exterior ∠’s. Substi ...
... Recall that adjacent interior/exterior angles are linear pairs. So, in a polygon with n-sides, there are also ____ vertices. Hence, there are also n pairs of _____________ angles. The sum of all of the polygon’s supplementary angles is______, which is the sum of the interior and exterior ∠’s. Substi ...
12.2 Part 1 Notes - Garnet Valley School District
... Objective: To apply properties of arcs and chords Definitions: Central Angle - __________________________________________________________ ...
... Objective: To apply properties of arcs and chords Definitions: Central Angle - __________________________________________________________ ...
6.1 Polygons - cloudfront.net
... • A polygon is a plane figure that is side formed by three or more segments called sides. (a closed, sided figure) • Each side intersects exactly two other sides at each of its endpoints. Each endpoint is a vertex of the polygon. • Two vertices that are endpoints of the same side are consecutive ver ...
... • A polygon is a plane figure that is side formed by three or more segments called sides. (a closed, sided figure) • Each side intersects exactly two other sides at each of its endpoints. Each endpoint is a vertex of the polygon. • Two vertices that are endpoints of the same side are consecutive ver ...
Geometry B Date: ______ 6.2 Properties of Parallelograms
... o Same-side (consecutive interior) angles are ____________________________ o Diagonals in a parallelogram _________________ one another. ...
... o Same-side (consecutive interior) angles are ____________________________ o Diagonals in a parallelogram _________________ one another. ...
12.1 Exploring Solids
... a. This is a polyhedron. It has 5 faces, 6 vertices, and 9 edges. b. This is not a polyhedron. Some of its faces are not polygons. c. This is a polyhedron. It has 7 faces, 7 vertices, and 12 edges. ...
... a. This is a polyhedron. It has 5 faces, 6 vertices, and 9 edges. b. This is not a polyhedron. Some of its faces are not polygons. c. This is a polyhedron. It has 7 faces, 7 vertices, and 12 edges. ...
SOLUTIONS TO PRACTICE MIDTERM LECTURE 1, SUMMER
... 6*. Axler, 5.13 (Hint: By problem 5.12, it is enough to show that every vector in V is an eigenvector of T . Say dim V = n. Let v ∈ V be nonzero and show that span(v) can be written as the intersection of some number of (n − 1)-dimensional subspaces of V , then use the second problem) Proof. Let dim ...
... 6*. Axler, 5.13 (Hint: By problem 5.12, it is enough to show that every vector in V is an eigenvector of T . Say dim V = n. Let v ∈ V be nonzero and show that span(v) can be written as the intersection of some number of (n − 1)-dimensional subspaces of V , then use the second problem) Proof. Let dim ...
Foundation - cndblessltd
... Solve more complex ratio and proportion problems, such as sharing out money between two groups in the ratio of their numbers ...
... Solve more complex ratio and proportion problems, such as sharing out money between two groups in the ratio of their numbers ...
histm008b
... decomposition of space into such tetrahedral, and the final three are assumptions that the decomposition is uniform throughout space, not changing if one moves from one point or vertex or face to another. One can actually get by with a much shorter list of underlying assumptions, but then the mathem ...
... decomposition of space into such tetrahedral, and the final three are assumptions that the decomposition is uniform throughout space, not changing if one moves from one point or vertex or face to another. One can actually get by with a much shorter list of underlying assumptions, but then the mathem ...
Grade 11 or 12 Pre
... Graph, with technology and using the primary trigonometric functions, the reciprocal trigonometric functions (i.e., cosecant, secant, cotangent) for angle measures expressed in radians, determine and describe key properties of the reciprocal functions (e.g., state the domain, range, and period, and ...
... Graph, with technology and using the primary trigonometric functions, the reciprocal trigonometric functions (i.e., cosecant, secant, cotangent) for angle measures expressed in radians, determine and describe key properties of the reciprocal functions (e.g., state the domain, range, and period, and ...
Matrices with a strictly dominant eigenvalue
... Proof. Assume A to be the transition matrix corresponding to a regular Markov chain. Because of Theorem 2.2 A has a positive discretely strictly dominant eigenvalue and a corresponding positive right eigenvector. Since all the column sums of A are 1, this eigenvalue is 1 according to Lemma 2.1. Beca ...
... Proof. Assume A to be the transition matrix corresponding to a regular Markov chain. Because of Theorem 2.2 A has a positive discretely strictly dominant eigenvalue and a corresponding positive right eigenvector. Since all the column sums of A are 1, this eigenvalue is 1 according to Lemma 2.1. Beca ...