
Uniform hyperbolicity of the curve graphs
... Recall that Proposition 3.1 of [B] gives a criterion for hyperbolicity depending on a constant, K, in the hypotheses. The three clauses (1), (2) and (3) of those hypotheses were verified respectively by Lemma 4.10, Proposition 4.11 and Lemma 4.9. These respectively gave K bounded by 4D, 18D and 2D, ...
... Recall that Proposition 3.1 of [B] gives a criterion for hyperbolicity depending on a constant, K, in the hypotheses. The three clauses (1), (2) and (3) of those hypotheses were verified respectively by Lemma 4.10, Proposition 4.11 and Lemma 4.9. These respectively gave K bounded by 4D, 18D and 2D, ...
GEOMETRIC SEARCHING PART 1: POINT LOCATION
... Planar embedding of planar graph G = (U,H) = mapping of each node in U to vertex in the plane and each arc in H into simple curve (edge) between the two images of extreme nodes of the arc, so that no two images of arc intersect except at their endpoints Every planar graph can be embedded in such a w ...
... Planar embedding of planar graph G = (U,H) = mapping of each node in U to vertex in the plane and each arc in H into simple curve (edge) between the two images of extreme nodes of the arc, so that no two images of arc intersect except at their endpoints Every planar graph can be embedded in such a w ...
Ordered Pairs - Hempfield Curriculum
... 2. If what Marcel thinks about his quadrilateral is true, what type of quadrilateral does he have? 3. Richelle drew hexagon KLMNOP at the right. She thinks the hexagon has six congruent angles. How can she show that the angles are congruent without using a protractor to measure them? ...
... 2. If what Marcel thinks about his quadrilateral is true, what type of quadrilateral does he have? 3. Richelle drew hexagon KLMNOP at the right. She thinks the hexagon has six congruent angles. How can she show that the angles are congruent without using a protractor to measure them? ...
Math : Real Number and Inequalities
... The quadratic is zero at 5 and 2 .These values divide the number line into three regions. Compile a table to show when the factors are positive and when negative. ...
... The quadratic is zero at 5 and 2 .These values divide the number line into three regions. Compile a table to show when the factors are positive and when negative. ...
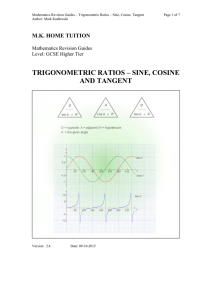
Trigonometric Ratios – Sine, Cosine, Tangent
... The graphs of sin x° and cos x° are similar to each other; in fact they are shown together for comparison. Both functions can only take values in the range -1 to +1, and both repeat themselves every 360°. Indeed, the graph of cos x° is the same as that of sin x° shifted 90° to the left. The graph of ...
... The graphs of sin x° and cos x° are similar to each other; in fact they are shown together for comparison. Both functions can only take values in the range -1 to +1, and both repeat themselves every 360°. Indeed, the graph of cos x° is the same as that of sin x° shifted 90° to the left. The graph of ...
Review for Ch. 5 and Ch 6
... Maria that she needs to study more regularly for her exams? For the next two problems, use the data in the table to make a line or bar graph. ...
... Maria that she needs to study more regularly for her exams? For the next two problems, use the data in the table to make a line or bar graph. ...
Dissections of polygons into convex polygons
... ones. However, Definition 1 is inconvenient and cannot be applied to a computer program. Our next aim is to find a more convenient (for the use of a computer) combinatorial characterization of topologically equivalent dissections. Let G be a graph of a dissection of a p0 -gon P0 into polygons. Then ...
... ones. However, Definition 1 is inconvenient and cannot be applied to a computer program. Our next aim is to find a more convenient (for the use of a computer) combinatorial characterization of topologically equivalent dissections. Let G be a graph of a dissection of a p0 -gon P0 into polygons. Then ...
DISTANCE EDUCATION M.Phil. (Mathematics) DEGREE
... Answer any FIVE questions. All questions carry equal marks. ...
... Answer any FIVE questions. All questions carry equal marks. ...
polypro P1
... polyhedron vertices V, faces F, and polyhedron edges E of a simply connected polyhedra. ...
... polyhedron vertices V, faces F, and polyhedron edges E of a simply connected polyhedra. ...
Maximizing Angle Counts for n Points in the Plane
... Among the general proofs for the maximum angle counts are certain Ө values that can be considered exceptions to this general proof. The general proof is considered to be the method of bounding the maximum angle count f(n, Ө), where n ≥ 4. Using this method, we simply maximize the number of triangles ...
... Among the general proofs for the maximum angle counts are certain Ө values that can be considered exceptions to this general proof. The general proof is considered to be the method of bounding the maximum angle count f(n, Ө), where n ≥ 4. Using this method, we simply maximize the number of triangles ...
Maths_Higher 9
... Calculate the area of a triangle given the length of two sides and the included angle Number – Combinations Use the product rule for counting (i.e. if there are m ways of doing one task and for each of these, there are n ways of doing another task, then the total number of ways the two tasks can ...
... Calculate the area of a triangle given the length of two sides and the included angle Number – Combinations Use the product rule for counting (i.e. if there are m ways of doing one task and for each of these, there are n ways of doing another task, then the total number of ways the two tasks can ...
Primary and Reciprocal Trig Ratios
... There are several special angles we can memorize the ratios for (Special triangles in grade 11). We refer to these as the related acute angles (R.A.A or R ) as we move forward in this unit. We memorize the ratios of these acute angles. ...
... There are several special angles we can memorize the ratios for (Special triangles in grade 11). We refer to these as the related acute angles (R.A.A or R ) as we move forward in this unit. We memorize the ratios of these acute angles. ...
Document
... A. $42.71 B. $44.71 C. $46.71 D. $56.71 8. A food company reduced the amount of salt in one of their food products from 700 milligrams to 630 milligrams. What is the percent decrease in the amount of salt in this food product? A. 10% B. 12% C. 70% D. 90% 9. Kyle caught 9 insects for his science proj ...
... A. $42.71 B. $44.71 C. $46.71 D. $56.71 8. A food company reduced the amount of salt in one of their food products from 700 milligrams to 630 milligrams. What is the percent decrease in the amount of salt in this food product? A. 10% B. 12% C. 70% D. 90% 9. Kyle caught 9 insects for his science proj ...
Geometric Concepts: Polygons, Quadrilaterals
... Equation – (5 minutes) If each vertex has two diagonals drawn from it and there are 5 vertices what is the total number of diagonals? (On the board write: 2 * 5 = 5) Wait to see if anyone reacts. What do you mean it’s not 10? We all know that 2 * 5 = 10 not 5! But we have to notice that the diagonal ...
... Equation – (5 minutes) If each vertex has two diagonals drawn from it and there are 5 vertices what is the total number of diagonals? (On the board write: 2 * 5 = 5) Wait to see if anyone reacts. What do you mean it’s not 10? We all know that 2 * 5 = 10 not 5! But we have to notice that the diagonal ...
COURSE TITLE: Algebra II - Trigonometry (Honors)
... * solve problems using prediction equation * graph lines of regression on a graphing calculator * identify and graph special functions * draw graphs of inequalities in two variables * write an inequality to solve problems C. Students will develop skills in solving and graphing systems of equations. ...
... * solve problems using prediction equation * graph lines of regression on a graphing calculator * identify and graph special functions * draw graphs of inequalities in two variables * write an inequality to solve problems C. Students will develop skills in solving and graphing systems of equations. ...
arXiv:math/0607084v3 [math.NT] 26 Sep 2008
... to it are invariant under the action of A. However, the operator A is not hyperbolic. Moreover, one can choose the vectors ω 1 and ω 2 to generate transcendental directions, thus preventing C from being invariant under the action of any hyperbolic integer operator. For n = 3 a stronger statement tha ...
... to it are invariant under the action of A. However, the operator A is not hyperbolic. Moreover, one can choose the vectors ω 1 and ω 2 to generate transcendental directions, thus preventing C from being invariant under the action of any hyperbolic integer operator. For n = 3 a stronger statement tha ...
GEOMETRY--2013
... “2” key. Choose a “mark” to be used to graph the points. You may choose the square, the cross, or the dot. VERY IMPORTANT: Before attempting to look at the graph, hit the ZOOM key on the top row and then scroll down to number 9, “ZoomStat”, and press enter. You should now see the ordered pairs you p ...
... “2” key. Choose a “mark” to be used to graph the points. You may choose the square, the cross, or the dot. VERY IMPORTANT: Before attempting to look at the graph, hit the ZOOM key on the top row and then scroll down to number 9, “ZoomStat”, and press enter. You should now see the ordered pairs you p ...
Blocking Coloured Point Sets
... This paper studies problems related to visibility and blocking in sets of coloured points in the plane. A point x blocks two points v and w if x is in the interior of the line segment vw. Let P be a finite set of points in the plane. Two points v and w are visible with respect to P if no point in P ...
... This paper studies problems related to visibility and blocking in sets of coloured points in the plane. A point x blocks two points v and w if x is in the interior of the line segment vw. Let P be a finite set of points in the plane. Two points v and w are visible with respect to P if no point in P ...



















![arXiv:math/0607084v3 [math.NT] 26 Sep 2008](http://s1.studyres.com/store/data/014838781_1-63e86760b3063903e159a8155f16fef1-300x300.png)

