Download Primary and Reciprocal Trig Ratios

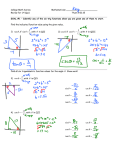
Primary and Reciprocal Trig Ratios
The primary trig ratios refer to the relationships between the sides and non-right angles in right-angled
triangles.
opp
hyp
adj
cos  
hyp
opp
tan  
adj
sin  
In standard position
sin θ =
cos θ =
tan θ =
The reciprocal trig ratios are as follows
csc  
1
sin 
sec  
1
cos 
cot  
1
tan 
sec  
hyp
adj
cot  
adj
hyp
and therefore it follows that :
csc  
hyp
opp
To find trig ratios, your calculator must be in the correct mode (degrees or radians)
Ex. 1
Find the following ratios rounded to 4 decimal places.
a)
cos(1.2164)
b)
tan( 0.4387)
c)
csc(1.6493)
It is important to recognize that it is the angle that you are taking the sin/cos/tan/csc/sec/cot of, and the ratio of
the sides in a related right angled triangle you are finding.
There are several special angles we can memorize the ratios for (Special triangles in grade 11). We refer to these as the
related acute angles (R.A.A or  R ) as we move forward in this unit. We memorize the ratios of these acute angles.
Special Angle #1.


4
These ratios can also be used to find exact trig ratios of angles sketched in other quadrants when
Ex. 2 Find cos  and csc  of the angle  
Special Angle # 2.

Again, the ratios of the angle

7
.
4
Special Angle # 3.
6


is the R.A.A.
4

3




and
can be used anytime an angle has a R.A.A. of
or
respectively.
6
3
6
3
Ex. 3 Sketch the following angles in standard position, and use your knowledge of the R.A.A. to find all 6
trig ratios for each.
2
9


a.
b.
3
4
Ex. 4 Find θ, given 0o ≤ θ ≤ 90o
1
a. sin  
2
b. sec  
2
3
More Angles in Standard Position
Recall: We can evaluate trig functions for angles greater than 90o or

radians by drawing the angle in
2
standard position and using the related acute angle (RAA).
Using the CAST rule
Ex. 1 Determine the exact measure of the indicated ratio for the given angle.
Ex.2 Determine the exact measure of the following using example 1 as a reference.
Ex. 3 The coordinates of a point on the terminal arm of a standard position angle, θ are (-2, 6). Find all six
trig ratios for this angle.
Sometimes, there is difficulty with finding trig ratios of angles that fall on one of the axes in standard position.
If we draw our angles in standard position as normal and think about the x, y and r values, we can determine
the corresponding trig ratios.
Homework:
1.
Evaluate.
a)
2.
sin120
b)
tan  150

sec  120
c)

d)
2
3
e)
Evaluate each of the following. Give exact answers.
a)
sin
g)
sin

6
7
b)
 tan
6

k)
2 sin
h)
2 cos 2
6
cos

6

5
4
cos

c)
4
h)
l)
6
1
i)
cos 2

3
tan

3
 csc 2

cos
i)
cot 3

4

2 sin cos
m) sin
4
4
2

2 
cos
j) 1  2 sin
3
2


3
d)
 tan 3
sin 540
sin

5
6
j)
4
2 
n)
cos
k)
sin 
3
e)
f)
cos

6
 sin
csc 390
cos
 sec
2 
3
4
3

3
o)
cos
2
3
3.
The coordinates of a point on the terminal arm of a standard position angle, θ are (5, -12). Find all six trig ratios for this angle.
4.
Determine
sin 
and
cot 
if
csc  
4
3
and
0    2 .
Answers to Homework
Graphs the Sine and Cosine Functions
Complete the following table for the function y = sinx and graph the function on the grid provided.
Characteristics of y = sinx
Key Points
Domain
Maximum Value
Minimum Value
Range
Period
Amplitude
Complete the following table for the function y = cosx and graph the function on the grid provided.
Characteristics of y = cosx
Key Points
Domain
Maximum Value
Minimum Value
Range
Period
Amplitude
Transformations of sin and cosine functions
y  a sin k ( x  p)  q
y  a cos k ( x  p )  q
a
k
p
q
Ex. 3 Write two possible equations for the graph shown.
y
5
x
π
2π
More Sine & Cosine Graphs and the Tangent Function
Recall: From Last Day
The base sine and cosine functions appear as follows
To graph transformations of these functions consider the effects of the following variables
Note: the angle must be in factored form to determine k
Graphing the Tangent Function, y = tan
Consider x, y and r values to determine the values of tan θ when θ is an angle on one of the axes.
In order to graph y = tan θ, we must consider the behaviour of the function around the undefined
values which represent vertical asymptotes on our graph.
Using these characteristics we
draw the tangent function
Characteristics of the Tangent Function
Graphs of Reciprocal Trigonometric Functions
How to graph the reciprocal functions:
1) Determine where the reciprocal function will intersect the primary function.
2) Determine and plot where Vertical asymptotes will be located. This will occur when the function
is undefined (denominator = 0).
3) Determine the behaviour of the graph as the function approaches vertical asymptotes.
The graph of y = csc x
Below is a graph of the function y = sin x. The reciprocal of this function is y = csc x, where csc x 
1
sin x
.
1) Functions intersect at
___________________________
2) Vertical Asymptotes at
___________________________
3) Behaviour around the asymptotes
Properties of y = csc x
Domain
Range
Period
The graph of y = sec x
Below is a graph of the function y = cos x. The reciprocal of this function is y = sec x, where sec x 
1
cos x
1) Functions intersect at
___________________________
2) Vertical Asymptotes at
___________________________
3) Behaviour around the asymptotes
Properties of y = sec x
Domain
Range
Period
The graph of y = cot x
Below is a graph of the function y = tan x. The reciprocal of this function is y = cot x, where cot x 
1
tan x
1) Functions intersect at
2) Vertical Asymptotes at
__________________________
3) Behaviour around the
asymptotes
*** Also consider zeros of y = cot x
Properties of y = cot x
Domain
Range
Period
Work: Sketch two periods of each of the following the following. Scale in radians.
1.
y   tan x  1
4.
y  sec( x  )
4


y  csc  x  
3

7.

2.
5.
8.
y  2sec x
y  csc x  2
3.
1

y  tan x
y  csc( x  )  1
6.
2
2


y  2 tan 3  x    1 (challenge)
4

Solving Trigonometric Equations
Some Tools for solving trig equations:
Ex. 1 Solve each equation for 0    2 .
a) sin  
c) sec
2
1
2
 2 0
b) 2cos   3  0
d) tan 2  1
Ex. 2 Solve for 0  x  360
b) 3 sec x – 5 = 0
a) cos x = 0.75
Practice Questions
1.
2.
3.
Solve. 0    2
a)
3sin  1  sin 
e)
tan   1
h)
sin  1  0
j)
cos  1  0
Solve.
a)
d)
g)
0  x  360
3sin x  2  0
7cos x  5  1
3sin x  4
cos 1  0
f)
sec  2
cot   3
i)
k)
csc  1  0
b)
b)
e)
h)
2csc x  5  0
cot x  5  0
cos 2x  1
2cos   3  0
g)
3csc  6  0
c)
l)
tan   
c)
f)
I)
2tan x  7
2sec x  3  9
sec x  3  2
c)
2sin
Solve 0    2
a)
2 sin 2  1
b)
3 cos 3  2

2
1  0
d)
2 cos  1
Solving Trig Equations Part II
Recall: Solving trig equations requires knowledge of Special Triangles and the CAST rule. In some cases, we
can also use our knowledge of the graphs of trig functions to help to solve equations. The graphs of
y = sin x, and y = cos x are shown below for convenience.
y
1
x
π/2
π
3π/2
2π
π/2
π
3π/2
2π
-1
y
1
x
-1
Ex. 1 Solve for  where 0    2
a) sin 2   1  0
b) 2 cos 2   5cos   2  0
c) 4sin 2   7 sin   3  0
Math 12
pg. 320 # 4ac, 11, 12, 14ac, 15 ac, 16
Applications of Trigonometric Functions Day 1
Ex. 1 In a harbour, the water depth at high tide is 6.3m and low tide is 2.3m. High tide occurs at 12 noon
while low tide occurs at 6:12 p.m.
Determine (using a sketch of the graph if helpful):
a) the mean depth
b) period
c) amplitude
d) an equation using the sine function that represents the depth of water in the harbour at time t
e) the depth of the water at 1 p.m.
f) when a ship that requires a depth of 3.3m of water can safely enter the harbour
Applications of Trigonometric Functions Day 2
Ex. 1 A Ferris wheel with a 10m diameter rotates once every 30 seconds.
Passengers get on at the lowest point of the ride (1m off the ground).
i.
Draw a graph showing height above the ground through the first two cycles.
ii.
Write an equation (using a sine function)
to express height as a function of time.
iii.
Calculate the height of the ride after 9s.
iv.
Between what times will the Ferris wheel be 9m or higher in the first revolution?
pg 369 # 6 - 9, 11a,15