Geometry – Circles ~1~ NJCTL.org
... Look for and make use of structure. MP8 Look for and express regularity in repeated reasoning. Unit Essential Question: Unit Enduring Understandings: Do “how” and “where” a line(s) Tangent lines intersect a circle at a single point. intersect a circle make a difference? The angle measure of an ...
... Look for and make use of structure. MP8 Look for and express regularity in repeated reasoning. Unit Essential Question: Unit Enduring Understandings: Do “how” and “where” a line(s) Tangent lines intersect a circle at a single point. intersect a circle make a difference? The angle measure of an ...
part-2-of-2-north-country-ccssm-hs-march-inservice
... Dilation is a Non-Rigid Transformation that preserves angle, but involves a scaling factor that affects the distance, which results in images that are similar to the original shape. G-SRT Cluster Headings dealing with Similarity: • Understand Similarity in terms of similarity transformations • Prove ...
... Dilation is a Non-Rigid Transformation that preserves angle, but involves a scaling factor that affects the distance, which results in images that are similar to the original shape. G-SRT Cluster Headings dealing with Similarity: • Understand Similarity in terms of similarity transformations • Prove ...
Geometry Level 3 Curriculum
... any quadratic equation in x into an equation of the form (x- p)2 = q that has the same solutions. Derive the quadratic formula from this form. Understand and apply theorems about circles CCSS.MATH.CONTENT.HSG.C.A.1 Prove that all circles are similar. CCSS.MATH.CONTENT.HSG.C.A.2 Identify and describe ...
... any quadratic equation in x into an equation of the form (x- p)2 = q that has the same solutions. Derive the quadratic formula from this form. Understand and apply theorems about circles CCSS.MATH.CONTENT.HSG.C.A.1 Prove that all circles are similar. CCSS.MATH.CONTENT.HSG.C.A.2 Identify and describe ...
Determining locus
... Discussion: 1) circles with equal radii; perpendicular bisector of O1O2 2) circles with different radii, disjoint or touching; see the construction 3) circles with different radii, partially overlapping; the arc of circle outside the union of the given circles 4) circles with different radii, one co ...
... Discussion: 1) circles with equal radii; perpendicular bisector of O1O2 2) circles with different radii, disjoint or touching; see the construction 3) circles with different radii, partially overlapping; the arc of circle outside the union of the given circles 4) circles with different radii, one co ...
Chapter 1 Test Review Period ______ 1. Two nonadjacent angles
... 16. The part of a line consisting of two points and all the points between them describes a: 17. A pair of adjacent angles whose noncommon sides are opposite rays describe: 18. Two rays with a common endpoint that form a line describe: 19. The part of a line that starts at an endpoint and extends fo ...
... 16. The part of a line consisting of two points and all the points between them describes a: 17. A pair of adjacent angles whose noncommon sides are opposite rays describe: 18. Two rays with a common endpoint that form a line describe: 19. The part of a line that starts at an endpoint and extends fo ...
2-5 / 2-6 Class Notes
... intersection is exactly one point. D. If two planes intersect, then their intersection is a line. ...
... intersection is exactly one point. D. If two planes intersect, then their intersection is a line. ...
1.1 Segment Length and Midpoints - Mrs. Harris
... Name and classify angles. Measure and construct angles and angle ...
... Name and classify angles. Measure and construct angles and angle ...
Geometry – Chapter 1
... 10.5 Find the lengths of segments of tangents and secants 10.6 Write equations of circles 10.7 Skip *Don’t forget to RETEST over OBJECTIVES < 75% before or after school. DO NOT WAIT!! It’s harder to retest the longer you are away from it!! ...
... 10.5 Find the lengths of segments of tangents and secants 10.6 Write equations of circles 10.7 Skip *Don’t forget to RETEST over OBJECTIVES < 75% before or after school. DO NOT WAIT!! It’s harder to retest the longer you are away from it!! ...
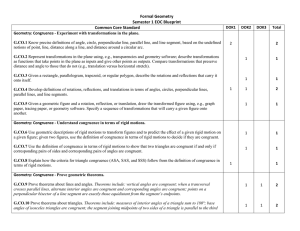
Formal Geometry Semester 1 EOC Blueprint Common Core
... crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. G.CO.10 Prove theorems about triangles. Theorems include: measures of interior angl ...
... crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. G.CO.10 Prove theorems about triangles. Theorems include: measures of interior angl ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.