Spherical Geometry Homework
... Given a line AB and a point C on it, there is exactly one point that is antipodal to C: D (think of the North and South Poles). All lines through these polar points are intersecting in two points C and D. Each of these intersecting lines is perpendicular to the line that is the “equator”. Try this o ...
... Given a line AB and a point C on it, there is exactly one point that is antipodal to C: D (think of the North and South Poles). All lines through these polar points are intersecting in two points C and D. Each of these intersecting lines is perpendicular to the line that is the “equator”. Try this o ...
Chapter 1 Vocabulary Geometry 2015 Sec 1-1 Points
... 6. Noncollinear – points that do NOT lie on the same line. 7. Coplanar – points that lie in the same plane. 8. Noncoplanar – points that do not lie in the same plane. ***The prefix “co” means together. The prefix “non” means not. **** 9. Intersection – a set of points common to two or more geometric ...
... 6. Noncollinear – points that do NOT lie on the same line. 7. Coplanar – points that lie in the same plane. 8. Noncoplanar – points that do not lie in the same plane. ***The prefix “co” means together. The prefix “non” means not. **** 9. Intersection – a set of points common to two or more geometric ...
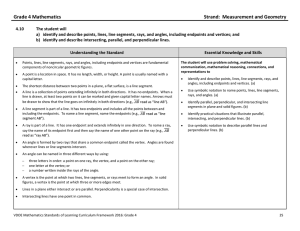
4.10 Curriculum Framework
... indicate that two lines are perpendicular. For example, the notation Students need experiences using geometric markings in figures to indicate congruence of sides and angles and to indicate parallel sides. Parallel lines lie in the same plane and never intersect. Parallel lines are always the same d ...
... indicate that two lines are perpendicular. For example, the notation Students need experiences using geometric markings in figures to indicate congruence of sides and angles and to indicate parallel sides. Parallel lines lie in the same plane and never intersect. Parallel lines are always the same d ...
Hyperboloids of revolution
... In considering the parabola as an ellipse with infinite eccentricity, the reasoning above applies word for word. Thus, every conic section may be considered as if it belonged to the hyperboloid. The preceding Theorem 10 is susceptible of the following interesting extension: An arbitrary plane P and ...
... In considering the parabola as an ellipse with infinite eccentricity, the reasoning above applies word for word. Thus, every conic section may be considered as if it belonged to the hyperboloid. The preceding Theorem 10 is susceptible of the following interesting extension: An arbitrary plane P and ...
MAT 201 Geometry
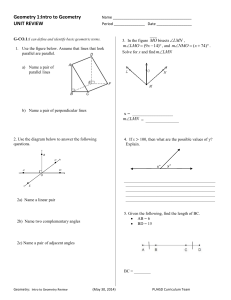
... 5. the point that two lines have in common 6. an angle that measures more than 90 degrees but less than L80 degrees 7. the point where the sides of an angle meet 8. an angle that measures L80 degrees 9. a point that divides a line segment into two congruent segments L0. lines in the same plane that ...
... 5. the point that two lines have in common 6. an angle that measures more than 90 degrees but less than L80 degrees 7. the point where the sides of an angle meet 8. an angle that measures L80 degrees 9. a point that divides a line segment into two congruent segments L0. lines in the same plane that ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.