Download jeopardy! - wuchevicha

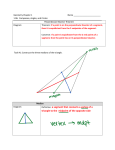
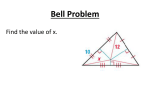
Unit 1 Review
Geometry
2010 – 2011
The
The
Is
Point Construct Solv
Buildin ‘Seg’ that
of
e
g
Way
an
that
it!
Blocks
angle? Triangle
!
We
All
Like
Change
100
100 100
100
100
100
100
200
200 200
200
200
200
200
300
300 300
300
300
300
300
1.
Any two _________ define a line.
2.
Any three ________ points define a plane.
3.
The intersection of two lines is a ________.
4.
The intersection of two planes is a _______.
5.
If two points lie on a plane, then the line
containing them _______________.
1.
2.
3.
4.
Name the intersection
of line n and segment
AI.
Name the intersection
of planes Q and MPT.
Name three coplanar
points in the figure.
Name plane Q another
way.

Show how the following are written by
providing an example:
Point
2. Line
3. Plane
4. Ray
5. Segment
6. Angle
1.

Line CD is the perpendicular bisector of
segment AB . If AM = 14, find AB.

Points Y, G, and B are located on a straight line.
B is between Y and G. If YB is 6 less 4 times the
length of BG, and YG = 34, find YB.

Find the length of the segment from -1782 to 577.

State the definitions of the following:
Acute angle
 Obtuse angle
 Reflex angle
 Right angle
 Straight angle


Describe the relationship between
angles a and b.
1.
2.
The intersection point of the angle bisectors of
the angles of a triangle is the center of the
____________________________ circle of the
triangle.
The intersection point of the perpendicular
bisectors of the sides of a triangle is the center
of the ______________________________ circle
of the triangle.

Explain how the following diagram was
created.

What are the special lines that run through the
vertex to the midpoint of the opposite side of a
triangle called?

[not on the test]

Draw the segment that represents the distance
from the point to the line.

Draw the perpendicular bisector of the
segment below.
1.
2.
Draw the angle bisector of the angle below.
Place point C in the INTERIOR of the angle.

Name all congruent segments.
E
F
A
B
C
D

If m∠XAC = 14x – 10 and m∠BAX = 46°, find
x.

Use the rule
T(x,y) = (-x , y)
to transform the
figure in the
coordinate plane at
the right.

Identify the transformation shown below.

Describe the transformation that results after
applying the rule T(x,y) = (x – 4, -y) to a figure
in the coordinate plane.

Use the rule T(x,y) = (x – 2, y + 1) to transform
the figure in the coordinate plane. Label your
image.