Survey
* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
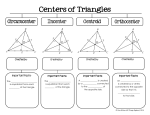
Download angle bisector equidistant in the interior equidistant incenter
Document related concepts
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Integer triangle wikipedia , lookup
Geometrization conjecture wikipedia , lookup
Perceived visual angle wikipedia , lookup
Rational trigonometry wikipedia , lookup
Trigonometric functions wikipedia , lookup
Line (geometry) wikipedia , lookup
Transcript
Geometry Section 5.3 Section 5.3: Use Angle Bisectors EQ: The length along the A ray that divides an perpendicular from a angle of 180o or less into 2 congruent angles pt. to a line Inscribed Circle Incenter (circumscribed triangle) The pt. of A circle that concurrency for a intersects each triangle's angle side of a triangle bisectors exactly one time angle bisector equidistant in the interior equidistant is on the angle bisector incenter to all of the sides equidistant Geometry Section 5.3 Geometry Section 5.3 67 0° Geometry Section 5.3 5.3 Summary:
