* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Section 5.3 ~ Angle Bisectors of Triangles
Survey
Document related concepts
Transcript
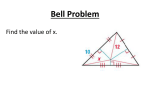
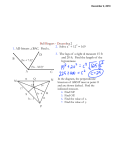
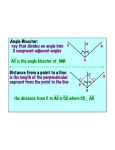
Section 5.3 ~ Angle Bisectors of Triangles Topics in this lesson: • incenter • Angle Bisector Theorem Objective: To understand what angle bisectors are and what relationships exist when they intersect inside a triangle. Vocabulary angle bisector a ray that divides an angle into two congruent angles *This is a Section 1.4 definition. ≅ ≅ incenter the point of concurrency of the three angle bisectors in a triangle *see picture on back side Angle Bisector Theorem If a point is on the bisector of an angle, then it is equidistant from the two sides of the angle. *Remember that the distance from a point to a line has to be the perpendicular connection. Converse of the Angle Bisector Theorem If a point is in the interior of an angle and is equidistant from the sides of the angle, then it lies on the bisector of the angle. *These theorems can be easily proven using congruent triangles and CPCTC. 5.3 Example 1 Find AD. Example 2 Find the measure of CBE. Example 3 Can you conclude that BD bisects ABC? Explain. a) b) Concurrency of Angle Bisectors of a Triangle The angle bisectors of a triangle intersect at a point that is equidistant from the sides of the triangle. INCENTER *Be very careful not to confuse this with the Concurrency of Perpendicular Bisectors in 5.2! 5.3 Example 4 Point G is the incenter. Find BG. Example 5 Find the value of x that makes N the incenter of the triangle. 5.3