* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Circumcenter point where perpendicular bisectors all meet Incenter
Euler angles wikipedia , lookup
Cartesian coordinate system wikipedia , lookup
Golden ratio wikipedia , lookup
Dessin d'enfant wikipedia , lookup
Multilateration wikipedia , lookup
Perceived visual angle wikipedia , lookup
History of trigonometry wikipedia , lookup
Line (geometry) wikipedia , lookup
Reuleaux triangle wikipedia , lookup
Trigonometric functions wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euclidean geometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
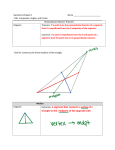
Review 6.26.5 Vocabulary to Review Perpendicular Bisector line, segment, or ray that is perpendicular to a segment, intersecting at the midpoint Angle Bisector line, segment, or ray that divides an angle into two congruent parts Isosceles Triangle 2 congruent sides (angles opposite these sides are also congruent) Equilateral Triangle all sides and angles congruent Scalene Triangle no sides are congruent Circumcenter point where perpendicular bisectors all meet Incenter point where angle bisectors all meet Median a line from a vertex to the midpoint of the opposite side Centroid point where medians all meet Altitude a line from a vertex perpendicular to the opposite side Orthocenter point where altitudes all meet Midsegment segment in a triangle whose endpoints are the midpoint of the two sides Find the equation of the perpendicular bisector of the line going through the given points. 1. (4, 4) and (6, 6) 2. (1, 1) and (7, 5) Determine if point C lies on the perpendicular bisector of AB. Prove your answer algebraically. 3. A (1, 3), B(7, 4), C(5, 7) Determine if the set of points creates an isosceles triangle. Prove your answer algebraically. 4. A(1, 0), B(3, 3), C(4, 0) 5. A(2, 1), B(2, 4), C(5, 4) 6. Find x and the length of each side. x + 2 2x 2 x + 4 7. In triangle RST, point P is the midpoint of RS, and point Q is the midpoint of RT. If PQ = n + 9 and ST = 3n 3, find the lengths of PQ and ST. Each figure shows a triangle with one or more of its medians. Each figure shows a triangle with one of its angle bisectors. This figure shows a triangle with its three angle bisectors intersecting at point P.