H-spaces II
... In this section we show that compact Lie groups other than SO(3)k × T l do admit special 1-tori. This implies that our theorem 1.4 is indeed stronger than theorem 1.1 of [8]. 5.1. Proposition. Let G be a compact connected Lie group which is not isomorphic to SO(3)k × T l . Then G has a subgroup isom ...
... In this section we show that compact Lie groups other than SO(3)k × T l do admit special 1-tori. This implies that our theorem 1.4 is indeed stronger than theorem 1.1 of [8]. 5.1. Proposition. Let G be a compact connected Lie group which is not isomorphic to SO(3)k × T l . Then G has a subgroup isom ...
Geometry Ch 1 Notes
... Postulate (axiom) – is a statement (basic assumption) assumed to be true without proof. Theorem – is a statement that has to be proved. Corollary – is a special case of a theorem. Basic Assumptions, the first Postulate – ...
... Postulate (axiom) – is a statement (basic assumption) assumed to be true without proof. Theorem – is a statement that has to be proved. Corollary – is a special case of a theorem. Basic Assumptions, the first Postulate – ...
Chapter 1 Study Guide
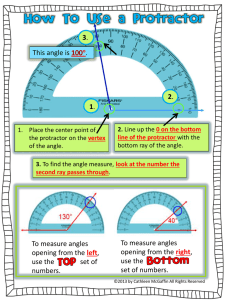
... 1. Two lines are _____________ if they intersect to form a right angle. 2. Two angles are ______________ if their measures have a sum of 90°. 3. When two rays intersect with a common endpoint a(n) ________________ is formed. 4. The ________________ is the point located halfway between the endpoints ...
... 1. Two lines are _____________ if they intersect to form a right angle. 2. Two angles are ______________ if their measures have a sum of 90°. 3. When two rays intersect with a common endpoint a(n) ________________ is formed. 4. The ________________ is the point located halfway between the endpoints ...
Solutions - UCI Math
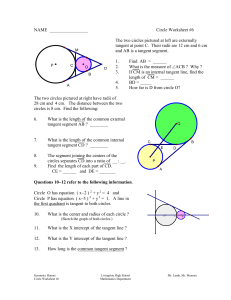
... Problem 2 (5 points). Let ABCD be a quadrilateral and let ` be a line that does not pass through any of the vertices A, B, C, or D. Prove that if ` intersects three sides of ABCD, then it also intersects the fourth side of ABCD. Solution. Without loss of generality, we may assume that ` intersects t ...
... Problem 2 (5 points). Let ABCD be a quadrilateral and let ` be a line that does not pass through any of the vertices A, B, C, or D. Prove that if ` intersects three sides of ABCD, then it also intersects the fourth side of ABCD. Solution. Without loss of generality, we may assume that ` intersects t ...
Logic Rules (2)
... unique line l incident with P and Q. I-2: For every line l there exist at least two distinct points that are incident with l. I-3: There exist three distince points with the property that no line is incident with all three of them. ...
... unique line l incident with P and Q. I-2: For every line l there exist at least two distinct points that are incident with l. I-3: There exist three distince points with the property that no line is incident with all three of them. ...
Section 9.1- Basic Notions
... 2. If two points lie in a plane, then the line containing the points lies in the plane. 3. If two distinct planes intersect, then their intersection is a line. 4. There is exactly one plane that contains any three distinct noncollinear points. 5. A line and a point not on the line determine a plane. ...
... 2. If two points lie in a plane, then the line containing the points lies in the plane. 3. If two distinct planes intersect, then their intersection is a line. 4. There is exactly one plane that contains any three distinct noncollinear points. 5. A line and a point not on the line determine a plane. ...
Geometry Fall 2013 Topics
... a. SSS, SAS, ASA, AAS, Hy-Leg criteria b. Isosceles triangle theorems [algebraic problems] c. Using more than one pair of congruent triangles, overlapping triangles d. Medians, altitudes, angle bisectors, and perpendicular bisectors e. Definition of similar polygons and AA similarity in triangles ** ...
... a. SSS, SAS, ASA, AAS, Hy-Leg criteria b. Isosceles triangle theorems [algebraic problems] c. Using more than one pair of congruent triangles, overlapping triangles d. Medians, altitudes, angle bisectors, and perpendicular bisectors e. Definition of similar polygons and AA similarity in triangles ** ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.