Download part-2-of-2-north-country-ccssm-hs-march-inservice

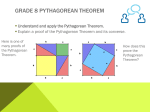
GRADE 8 PYTHAGOREAN THEOREM
 Understand and apply the Pythagorean Theorem.
 Explain a proof of the Pythagorean Theorem and its converse.
Here is one of
many proofs of
the Pythagorean
Theorem.
How does this
prove the
Pythagorean
Theorem?
GRADE 8 PYTHAGOREAN THEOREM
 Apply the Pythagorean Theorem to determine unknown side
lengths in right triangles in real-world and mathematical problems
in two and three dimensions.
 Apply the Pythagorean Theorem to find the distance between two
points in a coordinate system.
From
Kahn
Academy
GRADE 8 VOLUME
Solve real-world and mathematical problems involving volume of
cylinders, cones, and spheres.
 Know the formulas for the volumes of cones, cylinders, and
spheres and use them to solve real-world and mathematical
problems.
http://www.math.com
TURN AND TALK TO YOUR NEIGHBOR
What concepts and skills that HS Geometry have
traditionally spent a lot of time on are now being
introduced in middle school?
How does that change your ideas for focus in HS
Geometry?
What concepts and skills do you predict will be areas of
major focus in HS Geometry?
STRUCTURE OF THE HS GEOMETRY CONTENT STANDARDS
Congruence (G-CO)
Similarity, Right Triangles, and Trigonometry (G-SRT)
Circles (G-C)
Expressing Geometric Properties with Equations (G-GPE)
Geometric Measurement and Dimension (G-GMD)
Modeling with Geometry (G-MG)
STRUCTURE OF THE HS GEOMETRY CONTENT STANDARDS
Congruence (G-CO)
• Experiment with transformations in the plane
• Understand congruence in terms of rigid motions
• Prove geometric theorems (required theorems listed)
• Theorems about Lines and Angles
• Theorems about Triangles
• Theorems about Parallelograms
 Make geometric constructions (variety of tools and
methods…by hand and using technology) (required
constructions listed)
STRUCTURE OF THE HS GEOMETRY CONTENT STANDARDS
Similarity, Right Triangles, and Trigonometry (G-SRT)
• Understand Similarity in terms of similarity
transformations
• Prove theorems involving similarity
• Define trigonometric ratios and solve problems
involving right triangles
• (+) Apply trigonometry to general triangles
• Law of Sines
• Law of Cosines
STRUCTURE OF THE HS GEOMETRY CONTENT STANDARDS
Circles (G-C)
Understand and apply theorems about circles
• All circle are similar
• Identify and describe relationships among inscribed
angles, radii, and chords.
• Relationship between central, inscribed, and
circumscribed angles
• Inscribe angles on a diameter are right angles
• The radius of a circle is perpendicular to the tangent where
the radius intersects the circle
Find arc lengths and sectors of circles
STRUCTURE OF THE HS GEOMETRY CONTENT STANDARDS
Expressing Geometric Properties with Equations (G-GPE)
• Translate between the geometric description and the
equation for a conic section
• Use coordinates to prove simple geometric theorems
algebraically
STRUCTURE OF THE HS GEOMETRY CONTENT STANDARDS
Geometric Measurement and Dimension (G-GMD)
• Explain volume formulas and use them to solve
problems
• Visualize relationships between two-dimensional and
three-dimensional objects
Modeling with Geometry (G-MG)
• Apply geometric concepts in modeling situations
HS GEOMETRY CONTENT STANDARDS
Primarily Focused on Plane Euclidean Geometry
Shapes are studied Synthetically & Analytically
• Synthetic Geometry is the branch of geometry which makes
use of axioms, theorems, and logical arguments to draw
conclusions about shapes and solve problems
• Analytical Geometry places shapes on the coordinate
plane, allowing shapes to defined by algebraic equations,
which can be manipulated to draw conclusions about
shapes and solve problems.
FORMAL DEFINITIONS AND PROOF
HS Students begin to formalize the experiences with
geometric shapes introduced in K – 8 by
• Using more precise definitions
• Developing careful proofs
When you hear the word “proof”, what do
you envision?
INSTRUCTIONAL SHIFT:
MORE FOCUS ON TRANSFORMATIONAL PERSPECTIVE
Congruence, Similarity, and Symmetry are understood
from the perspective of
Geometric Transformation
extending the work that was started in Grade 8
INSTRUCTIONAL SHIFT:
MORE FOCUS ON TRANSFORMATIONAL PERSPECTIVE
Rigid Transformations (translations, rotations,
reflections) preserve distance and angle and therefore
result in images that are congruent to the original
shape.
G-C0 Cluster Headings Revisited
• Experiment with transformations in the plane
• Understand congruence in terms of rigid motions
• Prove geometric theorems
• Make geometric constructions
PROVING SIMILARITY VIA TRANSFORMATIONS
Dilation is a Non-Rigid Transformation that preserves
angle, but involves a scaling factor that affects the
distance, which results in images that are similar to
the original shape.
G-SRT Cluster Headings dealing with Similarity:
• Understand Similarity in terms of similarity
transformations
• Prove theorems involving similarity
PROVING SIMILARITY VIA TRANSFORMATIONS
From a transformational perspective…
Two shapes are defined to be similar to each other if
there is a sequence of rigid motions followed by a nonrigid dilation that carries one onto the other.
A dilation formalizes the idea of scale factor studied in
Middle School.
PROVE SIMILARITY BY TRANSFORMATIONS
What non-rigid transformation
proves that these triangles
are similar?
What is the center of dilation?
What is the scale factor of the
Dilation?
FIND SCALE FACTORS GIVEN A TRANSFORMATION
www.ck12.org Similarity Transformations Created by: Jacelyn O'Roark
CIRCLES IN ANALYTIC GEOMETRY
G-GPE (Expressing Geometric Properties with Equations)
 Derive the equation of a circle given center (3,-2) and radius 6 using the
Pythagorean Theorem
 Complete the square to find the center and radius of a circle with
equation x2 + y2 – 6x – 2y = 26
Think of the time spent in Algebra I on factoring
Versus completing the square to solve quadratic
Equations. What % of quadratics can be solved
by factoring? What % of quadratics can be
Solved by completing the square?
Is completing the square using the area model
more intuitive for students?
CONIC SECTIONS – CIRCLES AND PARABOLAS
• Translate between the geometric description and the equation for a conic section
• Derive the equation of a parabola given a focus and directrix
• Parabola – Note: completing the square to find the vertex of a parabola is in
the Functions Standards
(+) Ellipses and Hyperbolas in Honors or Year 4
Sketch and derive the equation for the parabola with
Focus at (0,2) and directrix at y = -2
Find the vertex of the parabola with equation
Y = x2 + 5x + 7
VISUALIZE RELATIONSHIPS BETWEEN 2-D AND 3-D OBJECTS
• Identify the shapes of 2-dimensional cross sections of 3dimensional objects
VISUALIZE RELATIONSHIPS BETWEEN 2-D AND 3-D OBJECTS
• Identify 3-dimensional shapes generated by rotations
of 2-dimensional objects
http://www.math.wpi.edu/Course_Materials/MA1022C11/volrev/node1.html
NORTH COUNTRY INSERVICE OUTLINE
• Review with Agreed Upon Expectations from 2-15-13 Inservice
– Share Experiences
• Review of CCSSM Practice Standards – Share Experiences
• Presentation of How Geometry Unfolds over K – 12 in CCSSM
• Focus on Volume Standard in HS Geometry
• Develop one unit focusing on HS Volume Standard and
Practice Standards
HS.GMD.A.1
Give an informal argument for the formulas for the
circumference of a circle, area of a circle, volume of a
cylinder, pyramid, and cone. Use dissection
arguments, Cavalieri’s principle, and informal limit
arguments.
INFORMAL ARGUMENT FOR AREA OF CIRCLE
http://www.youtube.com/watch?v=7zoqL2iOpvo
Area of Circle GeoGebra Applet
http://www.geogebratube.org/student/m279?mobile=true
From Don Steward
HS.GMD.A.3
Use volume formulas for cylinders, pyramids, cones, and
spheres to solve problems.★
Dan Meyer 3 Act: Popcorn Picker
Dan Meyer 3 Act: The Coffee Carrier
Dan Meyer 3 Act: You Pour, I Choose
Andrew Stadel 3 Act: Trashketball
MATHEMATICS ASSESSMENT PROJECT
H.G-GMD: Geometric measurement and dimension
Explain volume formulas and use them to solve problems
Equations of Circles 2
Evaluating Statements About Enlargements (2D and 3D)
Calculating Volumes of Compound Objects
ILLUSTRATIVE MATH G-GMD
G-GMD.3 Centerpiece
G-GMD.3 Doctor’s Appointment
MATHEMATICS ASSESSMENT PROJECT
Visualize relationships between two-dimensional and three- dimensional objects
4: Identify the shapes of two-dimensional cross-sections of three- dimensional
objects, and identify three-dimensional objects generated by rotations of twodimensional objects.
Modeling: Rolling Cups
2D Representations of 3D Objects
VOLUME ANIMATIONS
Charles A. Dana Center
Mathematics Unfolding: Volume
http://ccsstoolbox.agilemind.com/animations/standards_content_mathematics_volu
me.html
HS.GMD.B.4
Identify the shapes of two-dimensional cross-sections of
three-dimensional objects generated by rotations of
two-dimensional objects.
G-GMD.4 Tennis Balls in a Can
NORTH COUNTRY INSERVICE OUTLINE
• Review with Agreed Upon Expectations from 2-15-13
Inservice – Share Experiences
• Review of CCSSM Practice Standards – Share Experiences
• Presentation of How Geometry Unfolds over K – 12 in
CCSSM
• Focus on Volume Standard in HS Geometry
• Develop one unit focusing on HS Volume
Standard and Practice Standards