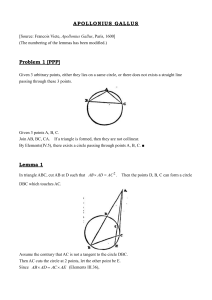
finite geometry and finite samples 1
... The number of points is finite. The number of lines is finite. Each line is on the same number s of points, where s≥2. Each point is on the same number t of lines, where t≥2. Each pair of distinct points is on at most one line. Each pair of distinct lines is on at most one point. Not all points are ...
... The number of points is finite. The number of lines is finite. Each line is on the same number s of points, where s≥2. Each point is on the same number t of lines, where t≥2. Each pair of distinct points is on at most one line. Each pair of distinct lines is on at most one point. Not all points are ...
1 Eves`s 25 Point Affine Geometry
... • We measure area in square units, such as square feet or square meters. This measurement is actually a ratio. For example, we might say that a square with side length of two feet is four square feet in size, because it is four times as big as a square with side length of one foot (which we call the ...
... • We measure area in square units, such as square feet or square meters. This measurement is actually a ratio. For example, we might say that a square with side length of two feet is four square feet in size, because it is four times as big as a square with side length of one foot (which we call the ...
Lesson 6 Day 1
... transversal and are outside the lines that the transversal intersects; sometimes called consecutive exterior angles • Same-side interior angles - angles that lie on the same side of the transversal and are in between the lines that the transversal intersects; sometimes called consecutive interior an ...
... transversal and are outside the lines that the transversal intersects; sometimes called consecutive exterior angles • Same-side interior angles - angles that lie on the same side of the transversal and are in between the lines that the transversal intersects; sometimes called consecutive interior an ...
3.1 The concept of parallelism
... Klein showed that there are three basically different types of geometry. In the Bolyai Lobachevsky type of geometry, straight lines have two infinitely distant points. In the Riemann type of spherical geometry, lines have no (or more precisely two imaginary) infinitely distant points. Euclidean geom ...
... Klein showed that there are three basically different types of geometry. In the Bolyai Lobachevsky type of geometry, straight lines have two infinitely distant points. In the Riemann type of spherical geometry, lines have no (or more precisely two imaginary) infinitely distant points. Euclidean geom ...
The School District of Palm Beach County GEOMETRY HONORS
... Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including t ...
... Make formal geometric constructions with a variety of tools and methods (compass and straightedge, string, reflective devices, paper folding, dynamic geometric software, etc.). Copying a segment; copying an angle; bisecting a segment; bisecting an angle; constructing perpendicular lines, including t ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.