What is Geometry? Understanding Angles
... Aim: What is Geometry? Do Now: Write an algebraic expression for each of this phrases: 3 more than w r decreased by 2 the product of 5r and s ...
... Aim: What is Geometry? Do Now: Write an algebraic expression for each of this phrases: 3 more than w r decreased by 2 the product of 5r and s ...
2014-2015. Geometry Curriculum
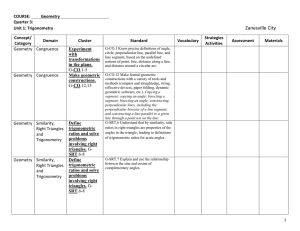
... G-GPE.B.4 Use coordinates to prove simple geometric theorems transformations using tools. Key Vocabulary algebraically. For example, prove or disprove that a figure Polygon I can find a sequence of transformations defined by four given points in the coordinate plane is a Convex that will carry a s ...
... G-GPE.B.4 Use coordinates to prove simple geometric theorems transformations using tools. Key Vocabulary algebraically. For example, prove or disprove that a figure Polygon I can find a sequence of transformations defined by four given points in the coordinate plane is a Convex that will carry a s ...
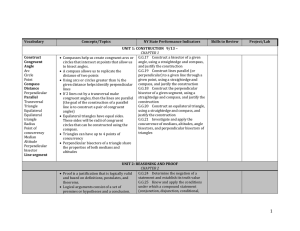
The parallel postulate, the other four and Relativity
... order that non of them contradicts any of the other postulates of what actually are or mean. In the manuscript is proved that parallel postulate is only in Plane (three points only) and is based on the four Postulates for Constructions, where all properties of Euclidean geometry compactly exist as E ...
... order that non of them contradicts any of the other postulates of what actually are or mean. In the manuscript is proved that parallel postulate is only in Plane (three points only) and is based on the four Postulates for Constructions, where all properties of Euclidean geometry compactly exist as E ...
key_terms_and_definitions
... Central Angle: an angle whose vertex is at the center of a circle Chord: a segment whose endpoints are on a circle Circumcenter: The point of intersection of the perpendicular bisectors of the sides of a given triangle; the center of the circle circumscribed about a given triangle. Circumscribed Cir ...
... Central Angle: an angle whose vertex is at the center of a circle Chord: a segment whose endpoints are on a circle Circumcenter: The point of intersection of the perpendicular bisectors of the sides of a given triangle; the center of the circle circumscribed about a given triangle. Circumscribed Cir ...
1 An introduction to homotopy theory
... defines a homotopy of paths γ0 ⇒ γ1 . Hence there is a single homotopy class of paths joining p, q, and so Π1 (X) maps homeomorphically via the source and target maps (s, t) to X × X, and the groupoid law is (x, y) ◦ (y, z) = (x, z). This is called the pair groupoid over X. The fundamental group π1 ...
... defines a homotopy of paths γ0 ⇒ γ1 . Hence there is a single homotopy class of paths joining p, q, and so Π1 (X) maps homeomorphically via the source and target maps (s, t) to X × X, and the groupoid law is (x, y) ◦ (y, z) = (x, z). This is called the pair groupoid over X. The fundamental group π1 ...
March Regional
... Geometry Team: Question 6 30 (that is, it rises units is situated at the top of a hill with an inclination of ...
... Geometry Team: Question 6 30 (that is, it rises units is situated at the top of a hill with an inclination of ...
Geometry, (2014) HMH Kanold, Burger, et al.
... interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. Similarity, Right Triangles, and Trigonometry — G-SRT A. ...
... interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. Similarity, Right Triangles, and Trigonometry — G-SRT A. ...
Chapter 6 Notes: Circles
... the circle. Any line segment connecting the center and a point on the circle is called a radius of a circle. All radii of a circle are congruent. A diameter of a circle is a chord that contains the center of the circle. The length of the diameter is twice that of the radius. Congruent circles are tw ...
... the circle. Any line segment connecting the center and a point on the circle is called a radius of a circle. All radii of a circle are congruent. A diameter of a circle is a chord that contains the center of the circle. The length of the diameter is twice that of the radius. Congruent circles are tw ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.