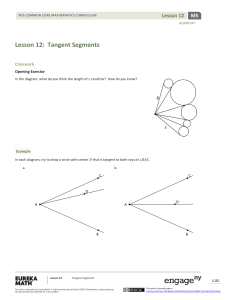
Geometry
... G-SRT.1a A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. G-SRT.1b The dilation of a line segment is longer or shorter in the ratio given by the scale factor. G-SRT.2 Given two figures, use the definiti ...
... G-SRT.1a A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. G-SRT.1b The dilation of a line segment is longer or shorter in the ratio given by the scale factor. G-SRT.2 Given two figures, use the definiti ...
Geometry Mathematics Curriculum Guide
... Relate work on parallel lines in G.GPE.5 to work on A.REI.5 in High School Algebra I involving systems of equations having no solution or infinitely many solutions • Review the concept of slope as the rate of change of the y-coordinate with respect to the x-coordinate for a point moving along a line ...
... Relate work on parallel lines in G.GPE.5 to work on A.REI.5 in High School Algebra I involving systems of equations having no solution or infinitely many solutions • Review the concept of slope as the rate of change of the y-coordinate with respect to the x-coordinate for a point moving along a line ...
Dividing a decimal by a whole number
... Topic VII Properties of Circles Vocabulary Circle - Is the set of all points in a plane equidistant from a given point called the center of the circle. Radius: Any segment with endpoints that are the center of the circle and a point on the circle. Chord: Segments with endpoints that are on the circ ...
... Topic VII Properties of Circles Vocabulary Circle - Is the set of all points in a plane equidistant from a given point called the center of the circle. Radius: Any segment with endpoints that are the center of the circle and a point on the circle. Chord: Segments with endpoints that are on the circ ...
2016-2017 Grade 10 Geometry Pacing Guide
... 9. [G-CO.9] Prove theorems about lines and angles. Theorems include vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidis ...
... 9. [G-CO.9] Prove theorems about lines and angles. Theorems include vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidis ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.