Circles Unit Guide Geometry - circles unit guide 5 22 14_2
... Make geometric constructions, understand and apply theorems about circles, find arc lengths and areas of sectors of circles, translate between the geometric description and the equation for a conic section, use coordinates to prove simple geometric theorems algebraically, and explain volume formulas ...
... Make geometric constructions, understand and apply theorems about circles, find arc lengths and areas of sectors of circles, translate between the geometric description and the equation for a conic section, use coordinates to prove simple geometric theorems algebraically, and explain volume formulas ...
Pearson Geometry Common Core
... 1. Derive the equation of a circle of given center SE/TE: 12.5: 798-803 and radius using the Pythagorean Theorem; complete the square to find the center and TE: 12.5: 803A-803B radius of a circle given by an equation. Use coordinates to prove simple geometric theorems algebraically 4. Use coordinate ...
... 1. Derive the equation of a circle of given center SE/TE: 12.5: 798-803 and radius using the Pythagorean Theorem; complete the square to find the center and TE: 12.5: 803A-803B radius of a circle given by an equation. Use coordinates to prove simple geometric theorems algebraically 4. Use coordinate ...
Q4 - Franklin County Community School Corporation
... 1. Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in t ...
... 1. Verify experimentally the properties of dilations given by a center and a scale factor: a. A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. b. The dilation of a line segment is longer or shorter in t ...
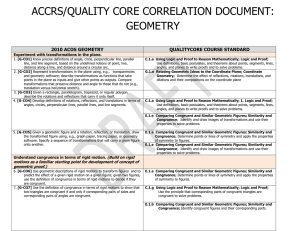
ACCRS/QualityCore-Geometry Correlation - UPDATED
... line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. 2. [G-CO2] Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane a ...
... line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc. 2. [G-CO2] Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane a ...
Topic VII Properties of Circles Topic VII Properties of Circles Topic VII
... The general rule for dilation by scale factor k with center of dilation at (a, b) is: Dk (x, y) = (a + k(x a), b + k(y b)) When the center of dilation is the origin, a = 0 and b = 0, so the rule simplifies to: Dk (x, y) = (kx, ky) As the radius of the circle increases from 1 to 3, the scale fact ...
... The general rule for dilation by scale factor k with center of dilation at (a, b) is: Dk (x, y) = (a + k(x a), b + k(y b)) When the center of dilation is the origin, a = 0 and b = 0, so the rule simplifies to: Dk (x, y) = (kx, ky) As the radius of the circle increases from 1 to 3, the scale fact ...
vii geometrical olympiad in honour of ifsharygin the
... number of these parts that can be angles? Solution. a) Answer. 3. Consider the convex envelope of all common points of given lines. Two lines passing through some vertex of this envelope divide the plane into four angles, and one of them contains all the remaining points. Thus the remaining lines do ...
... number of these parts that can be angles? Solution. a) Answer. 3. Consider the convex envelope of all common points of given lines. Two lines passing through some vertex of this envelope divide the plane into four angles, and one of them contains all the remaining points. Thus the remaining lines do ...
FOG Unit 5 Circles - CMS Secondary Math Wiki
... What are the line segments and angles that are related to circles? When lines intersect a circle or intersect within a circle, how do you find the measure of resulting angles, arcs, and segments? How can the distance formula (Pythagorean Theorem) be extended to derive the equation of a circle? How c ...
... What are the line segments and angles that are related to circles? When lines intersect a circle or intersect within a circle, how do you find the measure of resulting angles, arcs, and segments? How can the distance formula (Pythagorean Theorem) be extended to derive the equation of a circle? How c ...
Quarter 2
... G-SRT.A.01 Verify experimentally the properties of dilations given by a center and a scale factor: G-SRT.A.01.a A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. G-SRT.A.01.b The dilation of a line segme ...
... G-SRT.A.01 Verify experimentally the properties of dilations given by a center and a scale factor: G-SRT.A.01.a A dilation takes a line not passing through the center of the dilation to a parallel line, and leaves a line passing through the center unchanged. G-SRT.A.01.b The dilation of a line segme ...
The Parallel Postulate is Depended on the Other Axioms
... order that non of them contradicts any of the other postulates of what actually are or mean. In the manuscript is proved that parallel postulate is only in Plane (three points only) and is based on the four Postulates for Constructions, where all properties of Euclidean geometry compactly exist as E ...
... order that non of them contradicts any of the other postulates of what actually are or mean. In the manuscript is proved that parallel postulate is only in Plane (three points only) and is based on the four Postulates for Constructions, where all properties of Euclidean geometry compactly exist as E ...
Geometry –3-1
... Exchanging the hypothesis (IF) and conclusion (THEN) of a conditional statement. Postulate 3.5 If given a line and a point not on the line, ...
... Exchanging the hypothesis (IF) and conclusion (THEN) of a conditional statement. Postulate 3.5 If given a line and a point not on the line, ...
Glossary
... connected by arrows to show how each statement comes from the ones before it, and each reason is written below the statement it justifies. ...
... connected by arrows to show how each statement comes from the ones before it, and each reason is written below the statement it justifies. ...
circles - Welcome To Badhan Education
... If two sides of a cyclic quadrilateral are parallel, prove that remaining two sides are equal. ABCD is a cyclic quadrilateral. AB and DC when produced meet at E. Prove that EBC and EDA are equiangular. Two circles intersect each other at P and Q. From P diameters PA and PB are drawn to two circl ...
... If two sides of a cyclic quadrilateral are parallel, prove that remaining two sides are equal. ABCD is a cyclic quadrilateral. AB and DC when produced meet at E. Prove that EBC and EDA are equiangular. Two circles intersect each other at P and Q. From P diameters PA and PB are drawn to two circl ...
Geometry Glossary Essay, Research Paper Geometry Glossary
... - a set of points in which all segments connecting points of the set lie entirely in the set; There are three things one can do to see if a figure is convex – look for “dents”, extend the segments (they shouldn’t enter the figure), and connect any two points within the figure with a segment (if any ...
... - a set of points in which all segments connecting points of the set lie entirely in the set; There are three things one can do to see if a figure is convex – look for “dents”, extend the segments (they shouldn’t enter the figure), and connect any two points within the figure with a segment (if any ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.