elementary montessori geometry album
... Knowledge from Manipulation of Figures, Solid and Plane A Solid cannot be in two places at the same time A Solid as a state of matter Geometric Solid (three-dimensional) The surface of a solid The surface of a solid, the line and the point in the solid: from the solid to the point The point, the lin ...
... Knowledge from Manipulation of Figures, Solid and Plane A Solid cannot be in two places at the same time A Solid as a state of matter Geometric Solid (three-dimensional) The surface of a solid The surface of a solid, the line and the point in the solid: from the solid to the point The point, the lin ...
Scope Geometry Regular 2016-2017.xlsx
... Use coordinates to prove simple geometric theorems algebraically. Right Triangle • prove theorems about triangles, such as using triangle similarity to ...
... Use coordinates to prove simple geometric theorems algebraically. Right Triangle • prove theorems about triangles, such as using triangle similarity to ...
Geometry Unpacked Content
... What does this standard mean that a student will know and be able to do? G-CO.1 Definitions are used to begin building blocks for proof. Infuse these definitions into proofs and other problems. Pay attention to Mathematical practice 3 “Construct viable arguments and critique the reasoning of others: ...
... What does this standard mean that a student will know and be able to do? G-CO.1 Definitions are used to begin building blocks for proof. Infuse these definitions into proofs and other problems. Pay attention to Mathematical practice 3 “Construct viable arguments and critique the reasoning of others: ...
Math 487 Exam 2 - Practice Problems 1. Short Answer/Essay
... statement is being made about a neutral geometry (i.e. every postulates except the Euclidean parallel postulate holds). (a) Parallel lines exist. True. By Postulate 5a, there are at least 3 non-collinear points. By Postulate 1, given any two points, there is exactly one line that contains them. Ther ...
... statement is being made about a neutral geometry (i.e. every postulates except the Euclidean parallel postulate holds). (a) Parallel lines exist. True. By Postulate 5a, there are at least 3 non-collinear points. By Postulate 1, given any two points, there is exactly one line that contains them. Ther ...
geometry pacing guide - Kalispell Public Schools
... CONGRUENCE: Understand congruence in terms of rigid motion. CC.9-12.G.CO.6 Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if ...
... CONGRUENCE: Understand congruence in terms of rigid motion. CC.9-12.G.CO.6 Use geometric descriptions of rigid motions to transform figures and to predict the effect of a given rigid motion on a given figure; given two figures, use the definition of congruence in terms of rigid motions to decide if ...
File
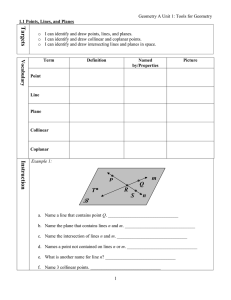
... e. What is another name for line n? _______________________________ f. Name 3 collinear points. _______________________________ ...
... e. What is another name for line n? _______________________________ f. Name 3 collinear points. _______________________________ ...
Geometry Strand
... 8.G.4 Determine angle pair relationships when given two parallel lines cut by a transversal 8.G.5 Calculate the missing angle measurements when given two parallel lines cut by a transversal 8.G.6 Calculate the missing angle measurements when given two intersecting lines and an angle ...
... 8.G.4 Determine angle pair relationships when given two parallel lines cut by a transversal 8.G.5 Calculate the missing angle measurements when given two parallel lines cut by a transversal 8.G.6 Calculate the missing angle measurements when given two intersecting lines and an angle ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.