Third Quarter - Wayne Local Schools
... the text says explicitly as well as inferences drawn from the text. CCSS.Math.Content.HSG-CO.2 Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Co ...
... the text says explicitly as well as inferences drawn from the text. CCSS.Math.Content.HSG-CO.2 Represent transformations in the plane using, e.g., transparencies and geometry software; describe transformations as functions that take points in the plane as inputs and give other points as outputs. Co ...
THE SHAPE OF REALITY?
... of two longitudinal segments from the north pole to the equator and a segment that goes one-fourth of the way around the equator. What are the angles at each vertex? Each one is 90°. So what is the sum of the three angles of that triangle on the sphere? 90° + 90° + 90° = 270°. Yikes! This result is ...
... of two longitudinal segments from the north pole to the equator and a segment that goes one-fourth of the way around the equator. What are the angles at each vertex? Each one is 90°. So what is the sum of the three angles of that triangle on the sphere? 90° + 90° + 90° = 270°. Yikes! This result is ...
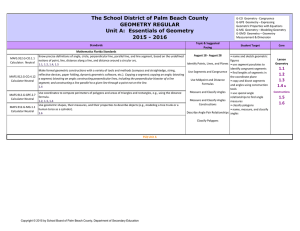
The School District of Palm Beach County GEOMETRY REGULAR
... transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). 6.6 *Not included on district assessment for this unit. Standard will be ...
... transformations as functions that take points in the plane as inputs and give other points as outputs. Compare transformations that preserve distance and angle to those that do not (e.g., translation versus horizontal stretch). 6.6 *Not included on district assessment for this unit. Standard will be ...
circles
... Solution : Let there be two circles which intersect at three points say at A, B and C. Clearly, A, B and C are not collinear. We know that through three non-collinear points A, B and C one and only one circle can pass. Therefore, there cannot be two circles passing through A, B and C. In other words ...
... Solution : Let there be two circles which intersect at three points say at A, B and C. Clearly, A, B and C are not collinear. We know that through three non-collinear points A, B and C one and only one circle can pass. Therefore, there cannot be two circles passing through A, B and C. In other words ...
Geometry and Constructions
... Some quadrangles have two pairs of parallel sides. These quadrangles are called parallelograms. Reminder: Two sides are parallel if they never meet, no matter how far they are extended. ...
... Some quadrangles have two pairs of parallel sides. These quadrangles are called parallelograms. Reminder: Two sides are parallel if they never meet, no matter how far they are extended. ...
Lines and Angles Lesson Plan
... Set up this first video by engaging students in a discussion of lines and angles in their lives. The horizon, an aerial view of the city, the proportions and shape of a desk, chair or door are the stuff of geometry. Geometry concepts require the understanding and use of precise terms. Show the video ...
... Set up this first video by engaging students in a discussion of lines and angles in their lives. The horizon, an aerial view of the city, the proportions and shape of a desk, chair or door are the stuff of geometry. Geometry concepts require the understanding and use of precise terms. Show the video ...
Unit 6: Day 1: Circle Geometry
... same length on the circle o fold each of these chords with a perpendicular bisector to find the centre of the circle o measure the distance from each chord to the centre of the circle Properties: o complete the following statements: 1. “If chords are congruent (equal), then they must be ____________ ...
... same length on the circle o fold each of these chords with a perpendicular bisector to find the centre of the circle o measure the distance from each chord to the centre of the circle Properties: o complete the following statements: 1. “If chords are congruent (equal), then they must be ____________ ...
3-5 - Nutley schools
... If two lines are cut by a transversal so that the consecutive interior angles are supplementary, then the lines are parallel. ...
... If two lines are cut by a transversal so that the consecutive interior angles are supplementary, then the lines are parallel. ...
Lie sphere geometry

Lie sphere geometry is a geometrical theory of planar or spatial geometry in which the fundamental concept is the circle or sphere. It was introduced by Sophus Lie in the nineteenth century. The main idea which leads to Lie sphere geometry is that lines (or planes) should be regarded as circles (or spheres) of infinite radius and that points in the plane (or space) should be regarded as circles (or spheres) of zero radius.The space of circles in the plane (or spheres in space), including points and lines (or planes) turns out to be a manifold known as the Lie quadric (a quadric hypersurface in projective space). Lie sphere geometry is the geometry of the Lie quadric and the Lie transformations which preserve it. This geometry can be difficult to visualize because Lie transformations do not preserve points in general: points can be transformed into circles (or spheres).To handle this, curves in the plane and surfaces in space are studied using their contact lifts, which are determined by their tangent spaces. This provides a natural realisation of the osculating circle to a curve, and the curvature spheres of a surface. It also allows for a natural treatment of Dupin cyclides and a conceptual solution of the problem of Apollonius.Lie sphere geometry can be defined in any dimension, but the case of the plane and 3-dimensional space are the most important. In the latter case, Lie noticed a remarkable similarity between the Lie quadric of spheres in 3-dimensions, and the space of lines in 3-dimensional projective space, which is also a quadric hypersurface in a 5-dimensional projective space, called the Plücker or Klein quadric. This similarity led Lie to his famous ""line-sphere correspondence"" between the space of lines and the space of spheres in 3-dimensional space.